计算机图形学图形旋转
计算机图形学| 翻译 (Computer Graphics | Translations)
Transformation techniques mean to modify the current shape or object in a particular manner. Changing of an object after creation, in terms of position or even size is known as translation. Here, we will be studying about how 2D translation is performed in computer graphics.
转换技术意味着以特定方式修改当前形状或对象。 创建后根据位置甚至大小更改对象的过程称为平移。 在这里,我们将研究如何在计算机图形学中执行2D翻译。
2D翻译 (2D Translation)
The translation is the movement in a straight line of an object from one position to another.
平移是对象从一个位置到另一位置沿直线的移动。
The movement of objects without deforming the shape of the object is Translation. Here the object is shifted from one position to another position and from one co-ordinate location to another.
在不变形对象形状的情况下移动对象就是平移。 在这里,对象从一个位置移动到另一位置,并从一个坐标位置移动到另一位置。
The translating polygon i.e. all vertex of the polygon is converted to a new position. Similarly, curved objects are translated. To change the position of the circle or ellipse its center coordinates are transformed, then the object is drawn using the new co-ordinates.
平移多边形(即多边形的所有顶点)将转换到新位置。 同样,弯曲的对象也可以平移。 要更改圆形或椭圆形的位置,请变换其中心坐标,然后使用新的坐标绘制对象。
Translation of point:
点的翻译:
To translate a point from coordinate position (x, y) to another (x, y), we add algebraically the translation distances Tx & Ty to the original co-ordinates.
为了将一个点从坐标位置(x,y)转换到另一个(x,y) ,我们将代数转换距离Tx & Ty代入原始坐标。
Translation equation:
翻译等式:
x1 = x + Tx
y1 = y + Ty
(The translation pair (Tx, Ty) is called as shift vector)
Example:
例:
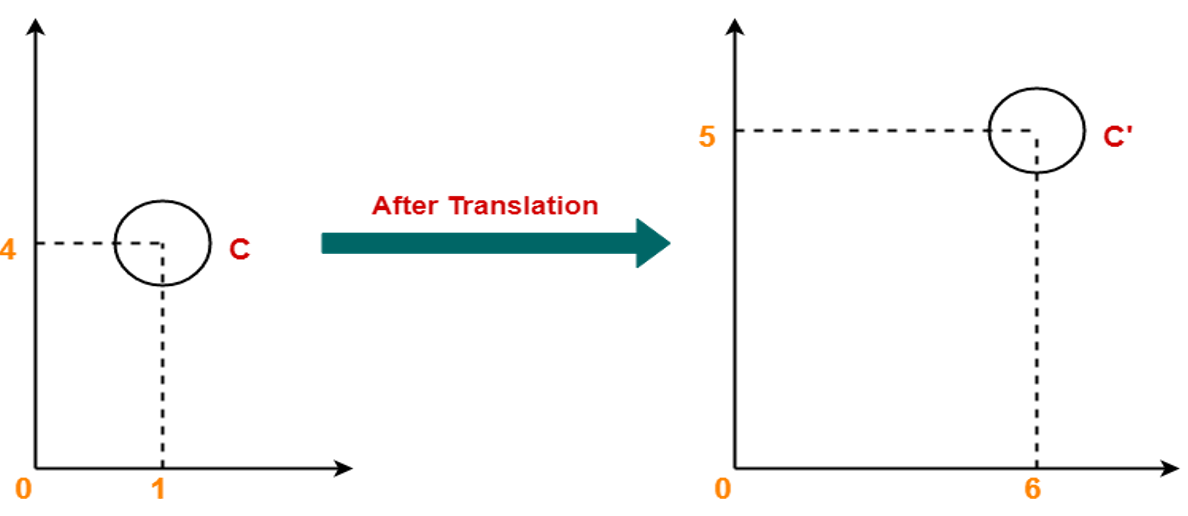
In the following image you can see that after applying translation, point C gets shifted to C'.
在下图中,您可以看到在应用平移之后,点C移至C' 。
Example:
例:
Given a square with coordinate points A (0, 3), B (3, 3), C (3, 0), D (0, 0). Apply the translation with distance 1 towards X axis and 1 towards Y axis. We have to find the new co-ordinates of the square.
给定一个具有坐标点A(0,3),B(3,3),C(3,0),D(0,0)的正方形。 将平移应用到X轴,距离1到Y轴。 我们必须找到正方形的新坐标。
Solution: Given-
解决方案:给定-
Old co-ordinates of the square = A (0, 3), B (3, 3), C (3, 0), D (0, 0)
正方形的旧坐标= A(0,3),B(3,3),C(3,0),D(0,0)
Translation vector = (Tx, Ty) = (1, 1)
翻译向量=(Tx,Ty)=(1,1)
对于坐标A(0,3) (For Coordinates A (0, 3))
Let the new coordinates of corner A = (Xnew, Ynew).
设角A的新坐标=(X new ,Y new )。
Applying the translation equations, we have-
应用平移方程式,我们有-
Xnew= Xold + Tx = 0 + 1 = 1
X 新 = X 旧 + T x = 0 + 1 = 1
Ynew= Yold + Ty = 3 + 1 = 4
Y 新 = Y 旧 + T y = 3 +1 = 4
Thus, New coordinates of corner A = (1, 4).
因此,角A的新坐标=(1,4)。
For Coordinates B (3, 3)
对于坐标B(3,3)
Let the new coordinates of corner B = (Xnew, Ynew).
令角B的新坐标=(X new ,Y new )。
Applying the translation equations, we have-
应用平移方程式,我们有-
Xnew= Xold + Tx = 3 + 1 = 4
X 新 = X 旧 + T x = 3 +1 = 4
Ynew= Yold + Ty = 3 + 1 = 4
Y 新 = Y 旧 + T y = 3 +1 = 4
Thus, New coordinates of corner B = (4, 4).
因此,角B的新坐标=(4,4)。
For Coordinates C (3, 0)
对于坐标C(3,0)
Let the new coordinates of corner C = (Xnew, Ynew).
令角的新坐标C =(X new ,Y new )。
Applying the translation equations, we have-
应用平移方程式,我们有-
Xnew= Xold + Tx = 3 + 1 = 4
X 新 = X 旧 + T x = 3 +1 = 4
Ynew= Yold + Ty = 0 + 1 = 1
Y 新 = Y 旧 + T y = 0 + 1 = 1
Thus, New coordinates of corner C = (4, 1).
因此,角C的新坐标=(4,1)。
For Coordinates D (0, 0)
对于坐标D(0,0)
Let the new coordinates of corner D = (Xnew, Ynew).
令角的新坐标D =(X new ,Y new )。
Applying the translation equations, we have-
应用平移方程式,我们有-
Xnew= Xold + Tx = 0 + 1 = 1
X 新 = X 旧 + T x = 0 + 1 = 1
Ynew= Yold + Ty = 0 + 1 = 1
Y 新 = Y 旧 + T y = 0 + 1 = 1
Thus, New coordinates of corner D = (1, 1).
因此,角D的新坐标=(1,1)。
翻译自: https://www.includehelp.com/computer-graphics/translations.aspx
计算机图形学图形旋转


中的视图)














函数与示例)

