1.ODE 选项摘要
解算 ODE 经常要求微调参数、调整误差容限或向求解器传递附加信息。本主题说明如何指定选项以及每个选项与哪些微分方程求解器兼容。
1.1 选项语法
使用 odeset 函数创建 options 结构体,然后将其作为第四个输入参数传递给求解器。例如,要调整相对和绝对误差容限,请使用以下命令:
opts = odeset('RelTol',1e-2,'AbsTol',1e-5);
[t,y] = ode45(@odefun,tspan,y0,opts); 如果您使用不带输入参数的 odeset 命令,MATLAB 将显示每个选项的可能值列表,并以花括号 {} 表示默认值。
odeget 函数可以查询现有结构体中的选项值,您可以用该函数来根据条件动态更改选项值。例如,以下代码检测 Stats 是否设置为 'on' ,并根据需要更改其值:
if isempty(odeget(opts,'Stats'))
odeset(opts,'Stats','on')
end1.2 选项与每个求解器的兼容性
在 odeset 中,有些选项是通用的,可与任何求解器兼容,还有一些选项是特定于求解器的。下表总结了每个选项与不同求解器之间的兼容性。
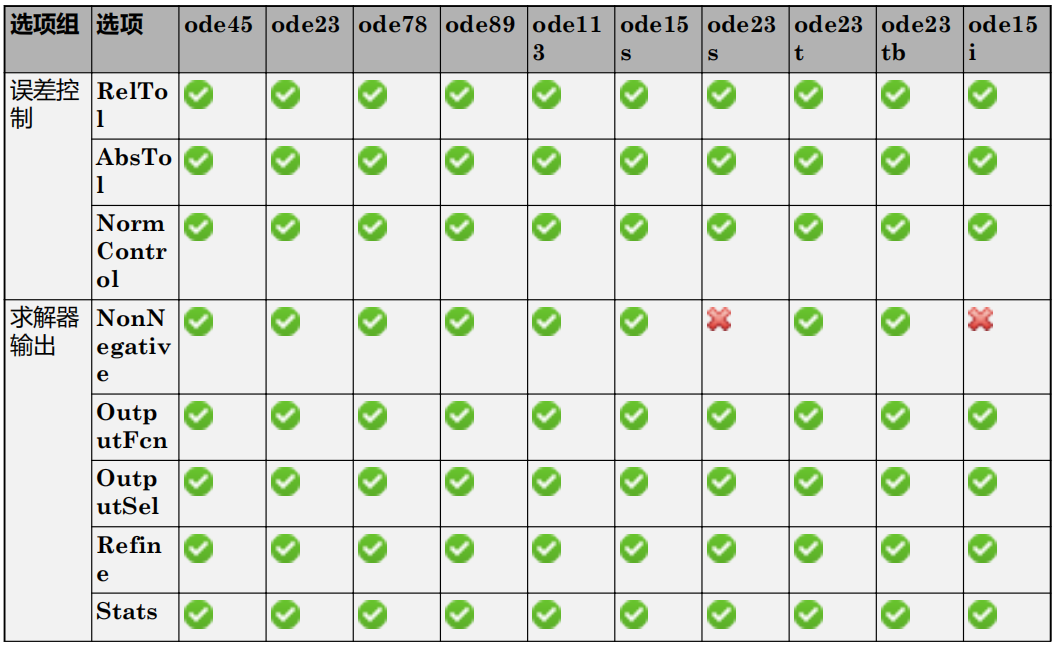

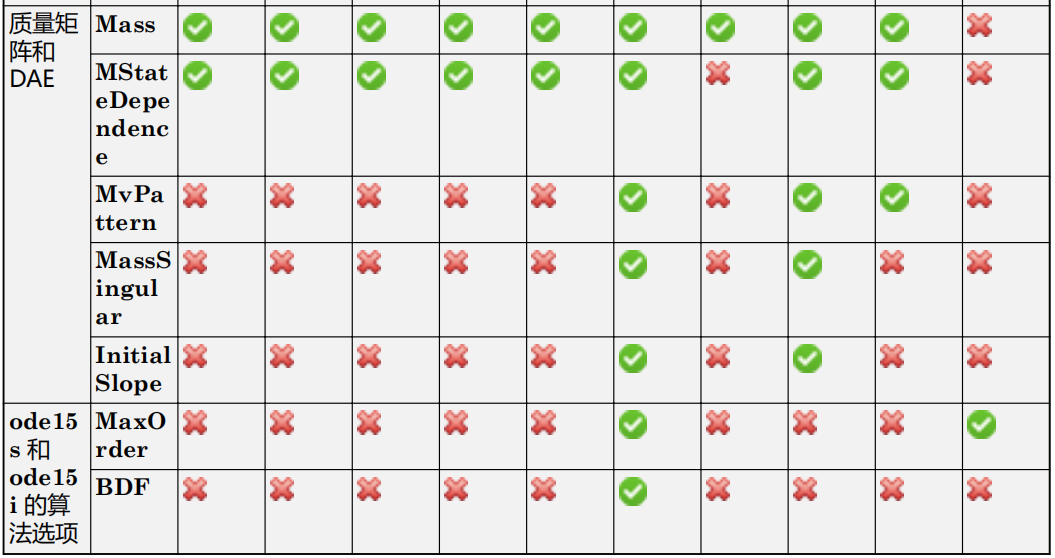
* 只有在解算不涉及质量矩阵的问题时,才对 ode15s 、 ode23t 和 ode23tb 求解器使用 NonNegative 参数。
** ode15i 的事件函数必须接受 yp 的第三个输入参数。
1.3 用法示例
MATLAB 包含几个示例文件,说明了如何使用各种选项。例如,键入 edit ballode 查看使用 'Events' 指定事件函数的示例,或键入 edit batonode 查看使用 'Mass' 指定质量矩阵的示例。有关示例文件及其使用的选项的完整总结,请参阅 “ODE 示例和文件摘要” 。
2.ODE 事件位置
2.1 什么是事件位置?
某些 ODE 方程组的解算难度部分在于确定停止求解的合适时间。积分区间中的最终时间可能由具体事件(而非数字)进行定义。从树上落下的苹果便是一个示例。ODE 求解器应当在苹果落地后立即停止,但您事前并不知道该事件会在何时发生。与之相似地,有些问题所涉及的事件则不会终止求解。沿行星轨道运行的卫星便是一个示例。这种情况下,您可能不希望提前停止积分,但仍希望检测到卫星每次围绕较大天体完成一个运行周期的时刻。
在 ODE 的求解过程中,使用事件函数来检测发生特定事件的时刻。事件函数采用您指定的表达式,并在该表达式等于零时检测事件。它们还能在检测到事件时提示 ODE 求解器停止积分。
2.2 编写事件函数
使用 odeset 函数的 'Events' 选项指定事件函数。事件函数必须具有一般形式
[value,isterminal,direction] = myEventsFcn(t,y)
在 ode15i 的情况下,事件函数还必须接受 yp 的第三个输入参数。
输出参数 value 、 isterminal 和 direction 均为向量,其第 i 个元素与第 i 个事件相对应:
• value(i) 是描述第 i 个事件的数学表达式。当 value(i) 等于零时发生事件。
• 如果当第 i 个事件发生时停止积分,则 isterminal(i) = 1 。否则为 0 。
• 如果需要查找全零值(默认值),则 direction(i) = 0 。值为 +1 时仅在事件函数递增的位置查找零,值为 -1 时仅在事件函数递减的位置查找零。指定 direction = [] 将对所有事件使用默认值 0。再次考虑苹果从树上落下的情形。表示落体的 ODE 为
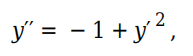
初始条件为 y 0 = 1 和 y ′ 0 = 0 。您可以使用事件函数来确定 y t = 0 的时刻,即苹果落地的时刻。对于此问题,检测苹果何时落地的事件函数为
function [position,isterminal,direction] = appleEventsFcn(t,y)
position = y(1); % The value that we want to be zero
isterminal = 1; % Halt integration
direction = 0; % The zero can be approached from either direction
end2.3 事件信息
如果指定了事件函数,则使用三个额外的输出参数调用 ODE 求解器,如下所示
[t,y,te,ye,ie] = odeXY(odefun,tspan,y0,options)
求解器返回的三个附加输出对应于检测到的事件:
• te 是发生事件的时刻的列向量。
• ye 包含 te 中的每个事件时刻对应的解值。
• ie 包含事件函数返回的向量的索引。这些值指示求解器检测到的事件。
您也可以使用单个输出来调用求解器,如下所示
sol = odeXY(odefun,tspan,y0,options)
这种情况下,事件信息以 sol.te 、 sol.ye 和 sol.ie 的形式存储在结构体中。
2.4 局限性
ODE 求解器采用的与事件函数配合使用的求根机制存在下列局限性:
• 如果在积分的第一步即发生终止事件,则求解器会将该事件记录为非终止事件并继续积分。
• 如果在第一步发生多个终止事件,则仅记录第一个事件,并且求解器会继续积分。
• 零值由每步之间的符号交叉确定。因此,对于两步间有偶数个交叉的函数而言,可能会错失其零值。如果求解器步长跨越了多个事件,请尝试减小 RelTol 和 AbsTol 以提高精度。也可以设置 MaxStep 以便为步长设置上限。调整 tspan 不会更改求解器所用的步长。
2.5 简单事件位置:弹球
此示例说明如何编写一个与 ODE 求解器配合使用的简单事件函数。示例文件 ballode 将模拟弹球的运动。事件函数在球每次弹起时停止积分,然后使用新的初始条件重新开始积分。在球的弹跳过程中,积分多次停止并重新开始。弹球的方程为

function [value,isterminal,direction] = bounceEvents(t,y)
value = y(1); % Detect height = 0
isterminal = 1; % Stop the integration
direction = -1; % Negative direction only 键入 ballode 以运行该示例并演示使用事件函数模拟球弹跳的过程。
ballode
2.6 高级事件位置:限制性三体问题
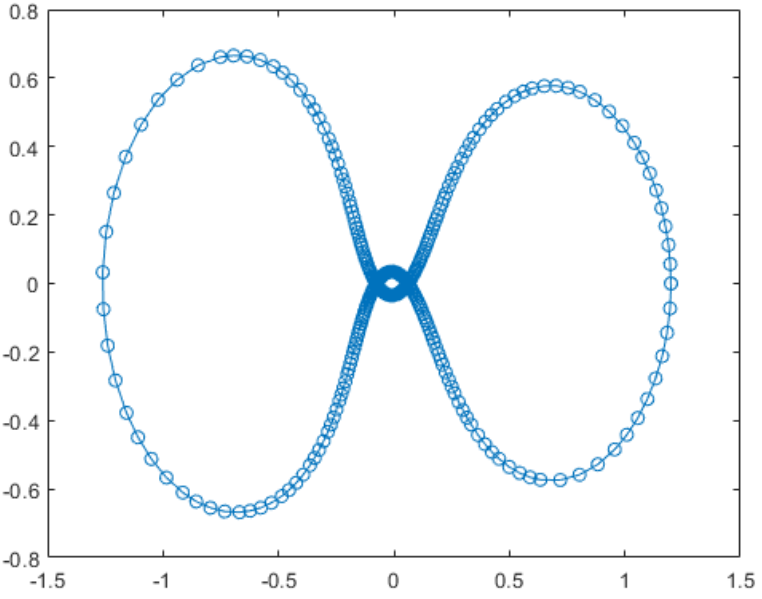
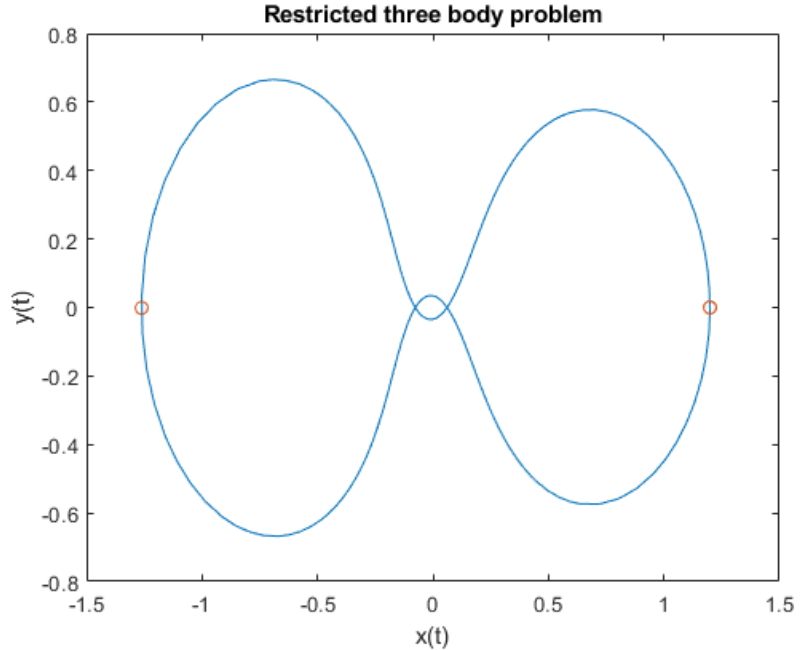
此示例说明如何使用事件函数的定向分量。示例文件 orbitode 模拟限制性三体问题,其中一个主体环绕两个大得多的主体做轨道运行。事件函数将确定轨道中距离环绕主体最近和最远的点。由于事件函数在轨道最近点和最远点的值相同,因此将使用过零的方向来区分二者。限制性三体问题的方程为
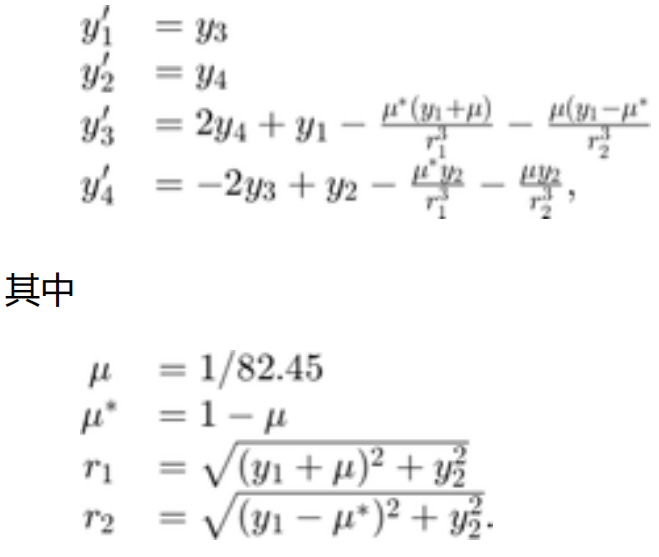
前两个解分量是微小物体的坐标,因此针对一个分量绘制另一个分量可以得到物体的轨迹。orbitode.m 中嵌套的事件函数将搜索两个事件。一个事件查找距离起点最远的点,另一个事件查找宇宙飞船返回到起点的点。即使积分器使用的步长并非通过事件位置确定,也会准确定位事件。在此示例中,指定过零方向的功能非常重要。返回到起点的点和距离起点最远的点具有相同的事件值,并由交叉方向来区分这两个点。为此行为编码的事件函数为
function [value,isterminal,direction] = orbitEvents(t,y)
% dDSQdt is the derivative of the equation for current distance. Local
% minimum/maximum occurs when this value is zero.
dDSQdt = 2 * ((y(1:2)-y0(1:2))' * y(3:4));
value = [dDSQdt; dDSQdt];
isterminal = [1; 0]; % stop at local minimum
direction = [1; -1]; % [local minimum, local maximum]
end 键入 orbitode 以运行该示例。
orbitode This is an example of event location where the ability to
specify the direction of the zero crossing is critical. Both
the point of return to the initial point and the point of
maximum distance have the same event function value, and the
direction of the crossing is used to distinguish them.
Calling ODE45 with event functions active...
Note that the step sizes used by the integrator are NOT
determined by the location of the events, and the events are
still located accurately.














)


)
)
