过拟合和欠拟合
什么是过拟合和欠拟合
过拟合:模型在训练集上效果好,在测试集上效果差
欠拟合:在训练集上效果就不好
产生过拟合的原因
- 参数太多,模型复杂度太高
- 数据量少,训练轮次过多
- 样本中噪声较大,模型拟合了噪声特征
过拟合解决方法
- 降低模型复杂度,使用小模型
- 增加样本数量,数据增强,减少训练轮次
- 使用正则项
正则项
正则化目的
平衡训练误差与模型复杂度,避免过拟合
L2正则项
L2正则就是在代价函数
迭代时,代价函数对参数求导:
可以看出L2正则化对偏置
每一次迭代过程中,参数
L1正则项
L1正则就是在代价函数
求导得
其中
比不使用正则项的更新规则多减了
为什么L1正则具有稀疏性
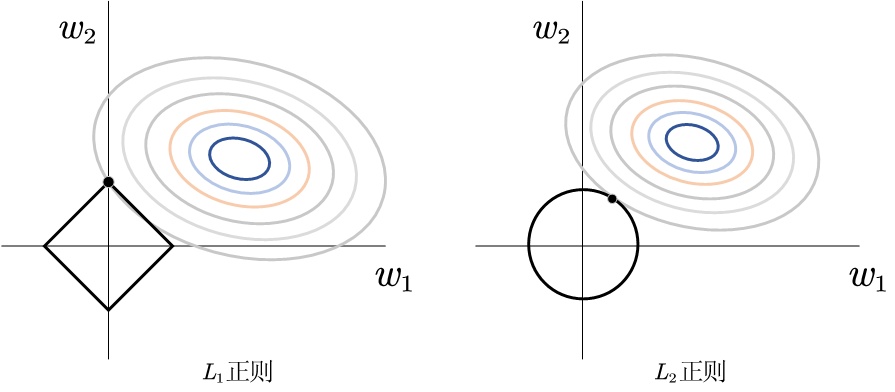
- 解空间角度
等值线表示损失函数,等值线越小的表示损失越小,交点处是优化后的参数情况。可以看出,正则项是对参数取值设置了约束条件,使得损失值不能超过约束范围。
L1正则有棱有角,更容易在顶点处相交(原因可以参考上一节的L1更新规则),此时
- 贝叶斯先验角度
参数模型表示为,数据样本
.则极大似然估计MLE可表示为
后验概率为
取对数后,
,我们在优化过程中,一般是求最小值,因此对
求最小值即可。将MLE表达式代入到后验概率中
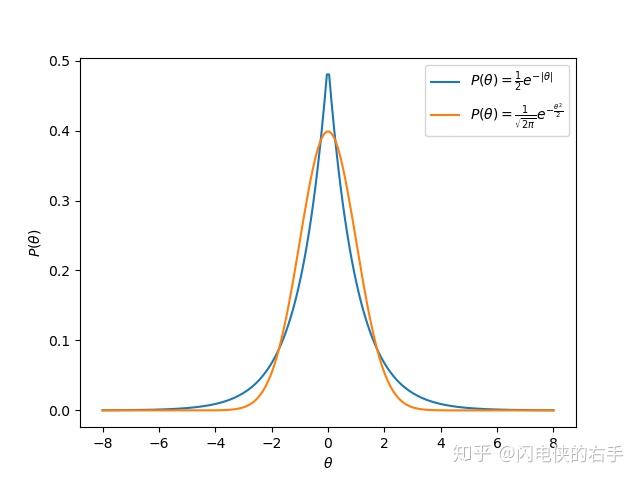
假设
优化函数相当于
假设
优化函数相当于
由图中可以看出,如果满足拉普拉斯分布,相比于高斯分布来说,参数



)















基本语法...)