题目：

打靶

小明参加X星球的打靶比赛。

比赛使用电子感应计分系统。其中有一局，小明得了96分。

这局小明共打了6发子弹，没有脱靶。

但望远镜看过去，只有3个弹孔。

显然，有些子弹准确地穿过了前边的弹孔。

不同环数得分是这样设置的：

1,2,3,5,10,20,25,50

那么小明的6发子弹得分都是多少呢？有哪些可能情况呢？

下面的程序解决了这个问题。

仔细阅读分析代码，填写划线部分缺失的内容。

public class Main

{

static void f(int[] ta, int[] da, int k, int ho, int bu, int sc)

{

if(ho<0 || bu<0 || sc<0) return;

if(k==ta.length){

if(ho>0 || bu>0 || sc>0) return;

for(int i=0; i

for(int j=0; j

System.out.print(ta[i] + " ");

}

System.out.println();

return;

}

for(int i=0; i<=bu; i++){

da[k] = i;

f(ta, da, k+1, __________________ , bu-i, sc-ta[k]*i); // 填空位置

}

da[k] = 0;

}

public static void main(String[] args)

{

int[] ta = {1,2,3,5,10,20,25,50};

int[] da = new int[8];

f(ta, da, 0, 3, 6, 96);

}

}注意：只填写划线处缺少的内容，不要填写已有的代码或符号，也不要填写任何解释说明文字等。

本题结论有待验证，证明后更改，主要纠结于3代表总共三个弹孔，还是三次重复穿过弹孔

如果代表总共三个弹孔  答案：i > 0  ? ho - 1: ho

如果代表总共三次重复穿过：答案：i > 1 ? ho - (i - 1) : ho

分析：

1.main函数分析：

public static void main(String[] args) {

int[] ta = { 1, 2, 3, 5, 10, 20, 25, 50 };//记录分值

int[] da = new int[8];//记录每个分值的个数

f(ta, da, k,ho,bu, sc);

f(ta, da, 0, 3, 6, 96);//第一二个参数不用解释，从ta第0位开始枚举，3个重复弹孔，上限6个分数，共96分

}

2.递归函数分析：

static void f(int[] ta, int[] da, int k, int ho, int bu, int sc) {

if (ho < 0 || bu < 0 || sc < 0)//最后ho bu sc 都大于0 才有递归的必要(剪枝)

return;

if (k == ta.length) {// 当k枚举完ta数组(类似for循环的i)，开始判断

if (ho > 0 || bu > 0 || sc > 0)// 三个参数都等于0，说明递归过程会把已经枚举的值扣除相应的ho，bu，sc值

return;

for (int i = 0; i < da.length; i++) {//输出每个分值

for (int j = 0; j < da[i]; j++)

System.out.print(ta[i] + " ");

}

System.out.println();

return;

}

for (int i = 0; i <= bu; i++) {//bu是分数个数的上限

da[k] = i;//每一个分值从0~bu(即6)进行深搜枚举

f(ta, da, k + 1, i > 1 ? ho - (i - 1) : ho, bu - i, sc - ta[k] * i); // 填空位置

}

/*刚开始直接填0，发现每个答案加起来就是96，唯一不同的就是，有的弹孔数不是3个

*可见，ho的值就是用来筛选的且要扣除有几个重复的，由da数组可知每个分值是记录每个分值个数的

*所以我推出ho,当分值的个数大于1，只要减去每个分值的个数扣掉1之后的值(即重复的数量)，如da[1] = 3,那么我就ho扣掉2

*最后运行，果然，得出了三组数据且只有三个弹孔，完美解决

* */

da[k] = 0;//分值每种情况枚举完之后要回溯，清零

}

把ho填0，得出的结果：

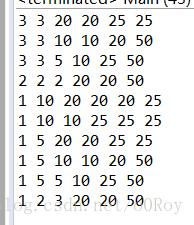
推出代码后结果：

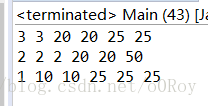
所以应该填入：i > 1 ? ho - (i - 1) : ho

完整代码：

public class Main {

static void f(int[] ta, int[] da, int k, int ho, int bu, int sc) {

if (ho < 0 || bu < 0 || sc < 0)

return;

if (k == ta.length) {

if (ho > 0 || bu > 0 || sc > 0)

return;

for (int i = 0; i < da.length; i++) {

for (int j = 0; j < da[i]; j++)

System.out.print(ta[i] + " ");

}

System.out.println();

return;

}

for (int i = 0; i <= bu; i++) {

da[k] = i;

f(ta, da, k + 1, i > 1 ? ho - (i - 1) : ho, bu - i, sc - ta[k] * i); // 填空位置

}

da[k] = 0;

}

public static void main(String[] args) {

int[] ta = { 1, 2, 3, 5, 10, 20, 25, 50 };

int[] da = new int[8];

f(ta, da, k,ho,bu, sc);

f(ta, da, 0, 3, 6, 96);

}

}

总结：

主要还是考深搜还有回溯，跟全排列有点像，类似全排列的进阶