基于 OpenYurt 和 EdgeX 的云边端协同新可能

2022 EdgeX 中国挑战赛暨中关村国际前沿科技创新大赛 EdgeX 专题赛正式拉开帷幕。本次大赛分设两大赛道：医疗、教育、消费行业赛道和能源、工业、供应链赛道。大赛致力于构建一个物联网及边缘计算的学习和分享平台，基于 EdgeX Foundry、OpenYurt 等开源技术，针对不同赛道的多个应用场景，以共享技术投资解决行业技术问题。

为帮助参赛选手更好地了解并运用相关技术，本次大赛将在 7 月至 9 月持续开展 3 轮技术培训，涵盖初、中、高不同层级，帮助开发者系统学习智能边缘系统知识。我们邀请到来自英特尔、VMware、阿里云等多家机构的技术专家进行分享。

边缘计算与边缘云原生

首先，熊峰专家为我们讲解了边缘计算与边缘云原生的详细定义。

边缘计算（Edge Computing）：

  • 是一种将工作负载部署在边缘的计算方式；
  • 是一种分散式运算架构，在靠近物、数据源或用户的地方进行应用计算与数据存储；
  • 核心目标：快速决策；
  • 四大驱动力：延迟/确定性，数据/带宽，有限的自治权，隐私/安全性；
  • 目前主要运用于汽车、农业、交通、医疗保健等行业。

图注：物联网与边缘计算

边缘计算根据对延迟的敏感度有两种定义的分层架构：Gartner 定义和 IDC 定义。

图注：Gartner 定义下的边缘计算分层架构

在 Gartner 定义中，边缘计算按延迟敏感度分层为：

  • Near Edge：非标准服务器或设备，在距离端侧最近的地方；
  • Far Edge：标准的 IDC，可以分三种类型：IDC、MEC、CDN 等；
  • Cloud：公共云或专有云服务，特征为资源集中、中心化管理。

图注：IDC 定义下的边缘计算分层架构

在 IDC 定义中，边缘计算按延迟敏感度分层为：

  • Heavy Edge：数据中心维度；集中式计算平台（CDN，自建 IDC）；
  • Light Edge：低功耗计算平台，适用于工业控制，数据处理、传输等物联网场景。

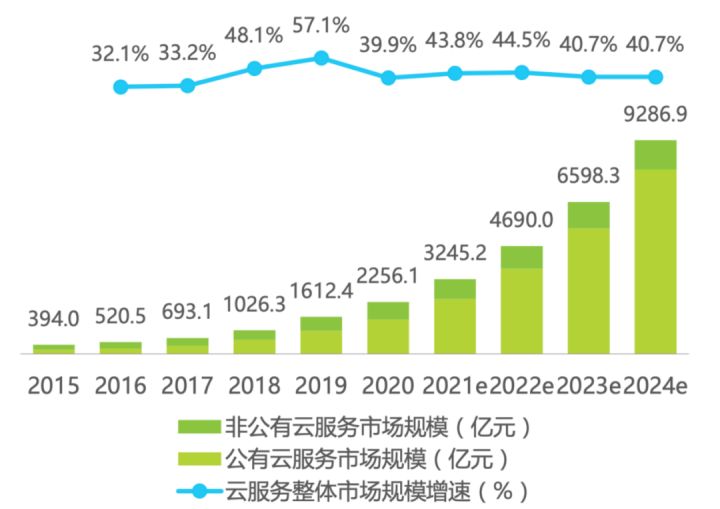
图注：2015 年至 2024 年（预测）公有与非公有云服务市场规模

目前，云原生用开放、标准的技术体系，敏捷的构建和运行高弹性、容错性好、易于管理的系统，帮助企业最大化利用云的能力，最大化发挥云的价值。云原生重构企业上云方式，企业上云成为常态。

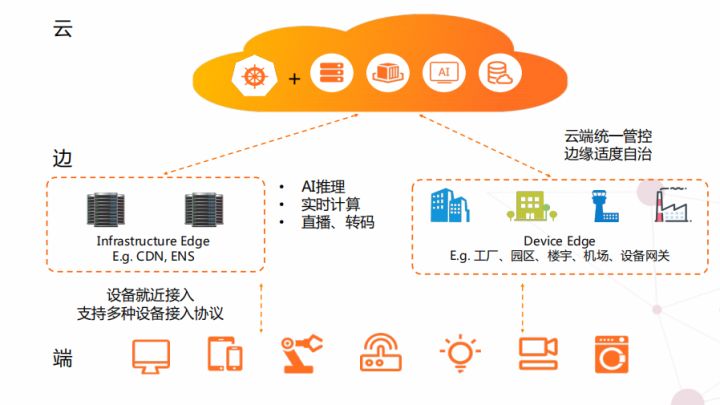
图注：云、边、端一体的边缘云原生架构

云原生加速了多云、云边融合，构建出云、边、端一体的边缘云原生架构。其中，边缘计算云边一体化基础设施因为具有以下特点被广泛运用：

  • 在边缘基础设施上提供和云上一致的功能和体验；
  • 云边运维协同、算力混编、网络协同等；
  • 云边的 DevOps 协同，业务快速边缘拓展；
  • 设备孪生，实现云边端的业务融合。

OpenYurt 云原生边缘计算平台架构

熊峰专家还为我们介绍了 OpenYurt 云原生边缘计算平台架构。

OpenYurt 是 CNCF 沙箱项目，提供云端管控、边缘自治的云边协同计算能力。通过与社区探索云原生物模型标准化，可扩展支持 EdgeX，LinkEdge 等物联网框架，支持多种物联网协议，实现设备孪生能力。

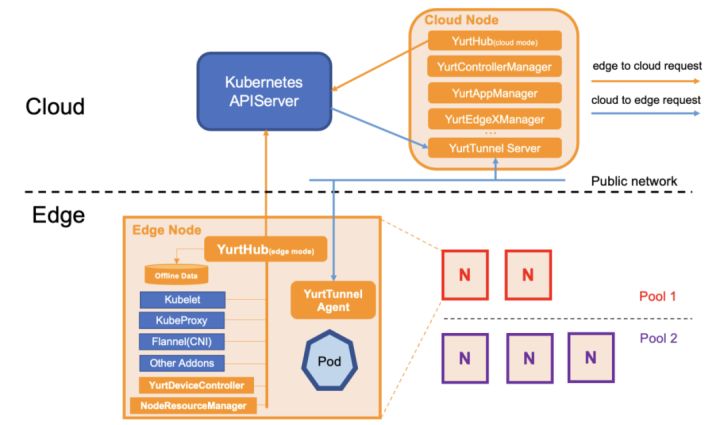
图注：OpenYurt 云原生边缘计算平台架构

OpenYurt 是基于 K8s 的边缘计算云原生智能平台项目，100% 兼容 K8s API，在 2020 年 5 月份开源，并在同年 9 月进入 CNCF 沙箱。

OpenYurt 理念：Extending your native Kubernetes to edge

目前，OpenYurt 已联合 VMware、Intel、深信服、招商局、浙大、天翼云等数家边缘计算方向产学研机构，共同推动 OpenYurt 发展，致力于成为边缘计算云原生方向事实标准。作为边缘计算云原生 PaaS 内核，OpenYurt 已经覆盖数十个行业、服务规模达数百万 CPU 核。

OpenYurt 具备完善的云边协同功能，具体分为云边运维协同与云边数据协同。

图注：OpenYurt 云边运维协同

图注：OpenYurt 云边数据协同

OpenYurt 也能与其他管理方法协同进行集群管控。

图注：OpenYurt DevOps 协同

图注：OpenYurt 单元化管理

图注：OpenYurt 单元化管理：NodePool

图注：OpenYurt 单元化管理: UnitedDeployment

在边缘计算场景下，云边交互可能弱网络连接。在断网或弱网状态下，边缘节点重启时原生 Kubernetes 无法恢复边缘业务。

为实现云边断网时，保障边缘业务的连续性与边缘业务跨节点通信的连续性，提出以下 OpenYurt 边缘自治的解决方案：

  • YurtHub 缓存节点数据，云边断网时，所有系统组件均从 YurtHub 中获取数据；
  • 业务容器重启时，Pod IP 保持不变；
  • 节点重启时，flannel vtep 的 MAC 地址保持不变。

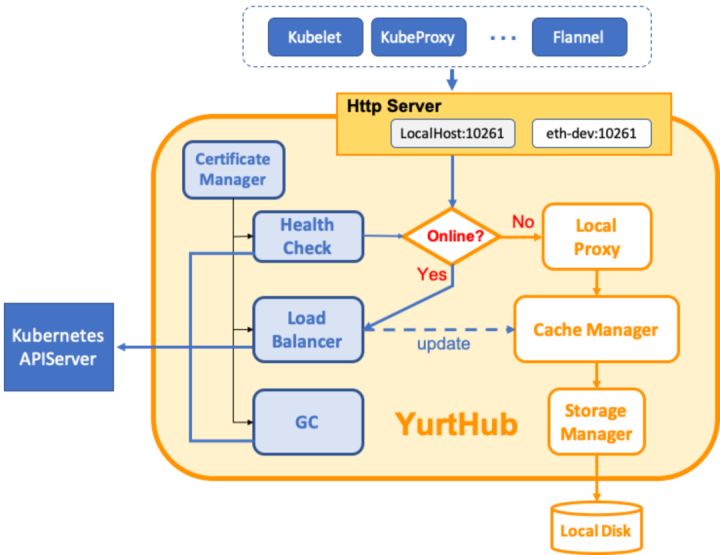
图注：OpenYurt 边缘自治方案

图注：OpenYurt 节点池治理方案

基于 OpenYurt+EdgeX Foundry 的云原生物模型及边缘设备管理实践

最后，熊峰专家介绍了如何结合使用 OpenYurt 和 EdgeX 物联网框架实现云原生物模型及边缘设备管理。

图注：OpenYurt+EdgeX，打通云边端一体化协同的最后一公里（EdgeX 2.1 LTS 支持）

OpenYurt+EdgeX 结合使用方案：

  • 使用 OpenYurt 编排部署 EdgeX Foundry；
  • 为管理现实世界中的设备，需要对设备管理相关的服务进行抽象，提供云原生 IoT 模型；
  • OpenYurt 通过集成 EdgeX Foundry 设备管理平台，支持端设备的管理能力；
  • 应用管理与设备管理路径统一云原生化。

了解更多&相关链接

[1] OpenYurt Github：

https://github.com/openyurtio

[2] OpenYurt概述：

https://openyurt.io/zh/docs/core-concepts/architecture

[3] tunnel与运维协同：

https://openyurt.io/zh/docs/core-concepts/yurttunnel

[4] raven与网络协同：

https://openyurt.io/zh/docs/core-concepts/raven

[5] 节点池与单元化：

https://openyurt.io/zh/docs/core-concepts/yurt-app-manager

[6] 云原生设备管理：

https://openyurt.io/zh/docs/core-concepts/yurt-device-controllerhttps://github.com/openyurtio/yurt-device-controller/blob/main/docs/yurt-device-controller-tutorial-v2.md

作者：EdgeX Foundry

原文链接

本文为阿里云原创内容，未经允许不得转载

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/510424.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

OSCAR 2022 开源产业大会PolarDB-X、 PolarDB-PG获奖揭晓

OSCAR 2022 开源产业大会PolarDB-X、 PolarDB-PG获奖揭晓

9月16日，OSCAR 2022 开源产业大会在京召开，会议由中国信息通信研究院、中国通信标准化协会主办，中国通信标准化协会云计算标准和开源推进委员会承办。此次会议以“千行百业 可信开源”为主题，邀请上百位专家大咖和国内主流的开源社…
阅读更多...
App 隐私合规“免费”自动化检测

App 隐私合规“免费”自动化检测

一、为什么要进行App隐私合规检测 2021年11月1日《个人信息保护法》正式生效；今年6月14日，国家互联网信息办公室公布《移动互联网应用程序信息服务管理规定》，这是针对App的最强监管新规，于8月1日起正式实施。新规要求应用程序提…
阅读更多...
跨模态学习能力再升级，EasyNLP 电商文图检索效果刷新 SOTA

跨模态学习能力再升级，EasyNLP 电商文图检索效果刷新 SOTA

导读 多模态内容（例如图像、文本、语音、视频等）在互联网上的爆炸性增长推动了各种跨模态模型的研究与发展，支持了多种跨模态内容理解任务。在这些跨模态模型中，CLIP（Contrastive Language-Image Pre-training&#x…
阅读更多...
EasyNLP 带你实现中英文机器阅读理解

EasyNLP 带你实现中英文机器阅读理解

导读 机器阅读理解是自然语言处理（NLP），特别是自然语言理解（NLU）领域最重要的研究方向之一。自1977年首次被提出以来，机器阅读理解已有近50年的发展史，历经“人工规则”、“传统机器学习”、“…
阅读更多...
一文剖析 PolarDB HTAP 的列存数据压缩

一文剖析 PolarDB HTAP 的列存数据压缩

前言 数据库迁移上云是大数据时代的一大趋势，PolarDB MySQL是阿里云自研的云原生数据库，主要处理在线事务负载(OLTP, OnLine Transactional Processing)，深受企业用户的青睐。当下，数据分析对于企业的重要性越发显著：…
阅读更多...
技术解读：现代化工具链在大规模 C++ 项目中的运用

技术解读：现代化工具链在大规模 C++ 项目中的运用

编者按：C 语言与编译器一直都在持续演进，出现了许多令人振奋的新特性，同时还有许多新特性在孵化阶。除此之外，还有许多小更改以提高运行效率与编程效率。本文整理自全球 C 及系统软件技术大会上的精彩分享，接下来由作者…
阅读更多...
如何将传统 Web 框架迁移部署到 Serverless 架构?

如何将传统 Web 框架迁移部署到 Serverless 架构?

与其说 Serverless 架构是一个新的概念，不如说它是一种全新的思路，一种新的编程范式。 但是原生的 Serverless 开发框架却非常少。以Web框架为例，目前主流的Web框架“均不支持Serverless模式部署”，因此我们一方面要尝试接触Serv…
阅读更多...
EasyNLP 发布融合语言学和事实知识的中文预训练模型 CKBERT

EasyNLP 发布融合语言学和事实知识的中文预训练模型 CKBERT

导读 预训练语言模型在NLP的各个应用中都有及其广泛的应用；然而，经典的预训练语言模型（例如BERT）缺乏对知识的理解，例如知识图谱中的关系三元组。知识增强预训练模型使用外部知识（知识图谱，字典…
阅读更多...
PolarDB-X 源码解读系列：DML 之 INSERT IGNORE 流程

PolarDB-X 源码解读系列：DML 之 INSERT IGNORE 流程

在上一篇源码阅读中，我们介绍了 INSERT 的执行流程。而 INSERT IGNORE 与 INSERT 不同，需要对插入值判断是否有 Unique Key 的冲突，并忽略有冲突的插入值。因此本文将进一步介绍 PolarDB-X 中 INSERT IGNORE 的执行流程，其根据插入…
阅读更多...
原根(详解+代码实现+例题+快速求解一个数的原根)

原根(详解+代码实现+例题+快速求解一个数的原根)

1.原根定义 假设一个数g对于P来说是原根&#xff0c;那么g^i mod P的结果两两不同,且有 1<g<P, 1<i<P,那么g可以称为是P的一个原根简单来说&#xff0c;g^i mod p ≠ g^j mod p &#xff08;p为素数&#xff09;其中i≠j且i, j介於1至(p-1)之间则g为p的原根。简单的…
阅读更多...
文娱行业搜索最佳实践

文娱行业搜索最佳实践

内容搜索的价值主要体现在两个方面&#xff1a; 对用户而言&#xff0c;用户将搜索作为寻找内容的工具&#xff0c;目标是“搜的到&#xff0c;搜的准”。用户更关心搜索结果的相关性、时效性和多样性。 对平台而言&#xff0c;搜索是内容消费、流量引导的核心入口&#xff0…
阅读更多...
一文搞懂 SAE 日志采集架构

一文搞懂 SAE 日志采集架构

日志&#xff0c;对于一个程序的重要程度不言而喻。无论是作为排查问题的手段&#xff0c;记录关键节点信息&#xff0c;或者是预警&#xff0c;配置监控大盘等等&#xff0c;都扮演着至关重要的角色。是每一类&#xff0c;甚至每一个应用程序都需要记录和查看的重要内容。而在…
阅读更多...
无需编写一行代码，实现任何方法的流量防护能力

无需编写一行代码，实现任何方法的流量防护能力

背景 微服务的稳定性一直是开发者非常关注的话题。随着业务从单体架构向分布式架构演进以及部署方式的变化&#xff0c;服务之间的依赖关系变得越来越复杂&#xff0c;业务系统也面临着巨大的高可用挑战。疫情期间&#xff0c;大家可能都经历过以下的场景&#xff1a; 线上预…
阅读更多...
使用日志上下文聚合插件使能上下文查询及 Livetail

使用日志上下文聚合插件使能上下文查询及 Livetail

背景 在排查业务故障时&#xff0c;用户往往需要查看业务日志文件来定位问题。然而&#xff0c;当用户在使用SLS收集业务日志时&#xff0c;同一个Logstore中往往存放着不同的日志&#xff08;例如同一台主机上不同目录下的文件&#xff0c;抑或是同一个K8S集群节点上不同容器…
阅读更多...
Koordinator v0.7: 为任务调度领域注入新活力

Koordinator v0.7: 为任务调度领域注入新活力

Koordinator[1]继上次v0.6版本[2]发布后&#xff0c;经过 Koordinator 社区的努力&#xff0c;我们迎来了具有重大意义的 v0.7 版本。在这个版本中着重建设了机器学习、大数据场景需要的任务调度能力&#xff0c;例如 Coscheduling、ElasticQuota 和精细化的 GPU 共享调度能力。…
阅读更多...
聊聊日志硬扫描，阿里 Log Scan 的设计与实践

聊聊日志硬扫描，阿里 Log Scan 的设计与实践

日志 Scan 的发展与背景 大数据快速增长的需要 泛日志&#xff08;Log/Trace/Metric&#xff09;是大数据的重要组成&#xff0c;伴随着每一年业务峰值的新脉冲&#xff0c;日志数据量在快速增长。同时&#xff0c;业务数字化运营、软件可观测性等浪潮又在对日志的存储、计算…
阅读更多...
注册配置、微服务治理、云原生网关三箭齐发，阿里云 MSE 持续升级

注册配置、微服务治理、云原生网关三箭齐发，阿里云 MSE 持续升级

背景 注册中心是日常使用频率很高的微服务组件&#xff0c;通过较低的资源溢价帮助客户缩短微服务的构建周期、提升可用性&#xff1b;微服务治理实现了 0 门槛就能接入全链路灰度、无损上下线、限流降级、环境隔离、数据库治理等能力&#xff0c;轻松完成开源到稳定生产的跨越…
阅读更多...
新零售标杆 SKG 全面拥抱 Serverless，实现敏捷交付

新零售标杆 SKG 全面拥抱 Serverless，实现敏捷交付

项目背景 SKG 公司是一家专注于高端健康产品的研发、设计与制造的企业。专注为消费者提供精致、时尚的高端产品&#xff0c;以及极致的按摩仪产品体验。 随着市场需求的迅速变化&#xff0c;SKG 的 IT 系统也逐渐面临着库存不准确、线上线下渠道无法协同、部署架构不灵活、IT…
阅读更多...
Mobius函数计算 定义+代码模板

Mobius函数计算 定义+代码模板

Mobius函数定义为&#xff0c;输入一个正整数N&#xff0c;当N1时&#xff0c;函数值为1&#xff0c;当N不为1时&#xff0c;首先在稿纸上将它分解质因数&#xff0c;若某质因数的个数大于1&#xff0c;则函数值为0&#xff0c;如N45&#xff0c;453*3*5,3出现了两次&#xff0…
阅读更多...
不仅有0.0075元的深度冷归档，更有对下一代云存储的重新定义

不仅有0.0075元的深度冷归档，更有对下一代云存储的重新定义

前言&#xff1a;重新定义下一代云存储&#xff0c;需要继续保障稳定、安全、可靠和低成本&#xff0c;进一步演进 Serverless 能力&#xff0c;智能适配负载变化&#xff0c;提供智能数据管理能力以及全场景覆盖不断发展的新负载。 阿里云存储的创新活力&#xff0c;不仅拓展了…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023