二维码的纠错码原理及细节

参考文档：

https://www.thonky.com/qr-code-tutorial/error-correction-coding

1. 消息多项式

消息多项式的系数组成：数字码字。如“hello world” ,利用二维码的编码原理，转换成十进制数字为“32, 91, 11, 120, 209, 114, 220, 77, 67, 64, 236, 17, 236, 17, 236, 17”，因此，这个语句的消息多项式为：

2. 生成多项式

生成多项式可以用下面这个式子概括：

n是生成的纠错码字的数量，α一般默认为2。为了方便进行多项式的出发，我们需要对生成多项式进行展开。

拿最简单的n=2举个例子（以下大部分步骤都是废话）：

因为α默认为2，而且在GF(256)中，加法用异或操作，所以

这样就得到生成多项式了。

注意，在这里的指数大于255也是不行的，一旦超过255，就要通过对255取模的方式来降一降。

从下面这个网址可以轻松得到n≥7的时候的生成多项式

https://www.thonky.com/qr-code-tutorial/generator-polynomial-tool?degree=7

注：GF(256)是啥？QR Code标准表示使用逐位模2算术和逐字节模100011101算法,也就是使用伽罗瓦域2^8，或者伽罗瓦域256，有时写为GF(256)。GF(256)的范围是0~255。简而言之，在这个神奇的领域里面，超过255是不允许的，一旦超过就要通过异或的方式来降一降。比如说2^8=256，因此需要和100011101进行异或操作来得到最终的值，所以2^8=256^285=58。2^9=58*2=116。2^10=116*2=232。……

3.进行除法

将生成多项式除以消息多项式来得到最后的结果。普通的多项式除法一般大家以前都接触过，但在这里不是在乘法步骤之后减去，而是执行XOR（在GF（256）中，其实就是一样的）。
就不多介绍。

步骤可以分为以下三步：

1. 找到适当的项乘生成多项式，使得乘法的结果与消息多项式具有相同的第一项。

2. 使用消息多项式（在第一个乘法步骤中）或余数（在所有后续乘法步骤中）对结果进行异或。

3. 执行这些步骤n次，其中n是消息多项式中的系数。

在进行两个多项式的除法之后，将有一个余数。该余数的系数是纠错码字。

拿完整的消息多项式和生成多项式做一个例子。

完整的消息多项式如下（Hello world的例子）：

为了确保在除法期间引导项的指数不会变得太小，将消息多项式乘以x^n，n是所需的纠错码字的数量。如当纠错码字的数量是10时，上式应该变成：

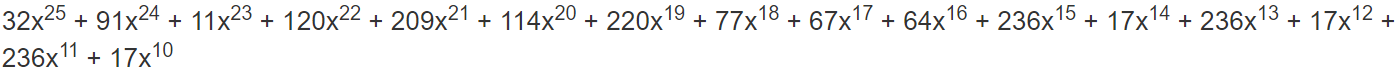
生成多项式的前导项也应该具有相同的指数，因此生成多项式也乘x^15得到下式（这里的原始生成多项式可以从上面给的链接里面轻松得到）

具体开始步骤：

1. 将生成多项式乘以消息多项式的前导项。消息多项式的前导项是32，也就是α^5，乘上生成多项式后，生成多项式变成

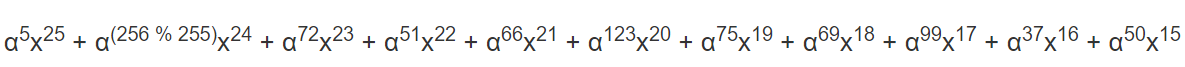
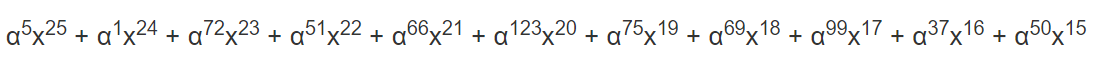
注意，指数的值不能超过255，一旦超过就要进行对255取模的操作。

可以明显看出经过上面这些步骤（保持指数相同，将消息多项式的前导码乘到生成多项式上），生成多项式和信息多项式拥有了完全相同的第一项。

2. 使用消息多项式对结果进行异或；从下面这个式子也可以看出来，就是消息多项式和生成多项式中相同次数的项的系数进行了异或操作，经过这个操作之后，消息多项式中最高次数的项已经没有了（因为生成多项式和消息多项式拥有完全相同的第一项，一异或就没了）。

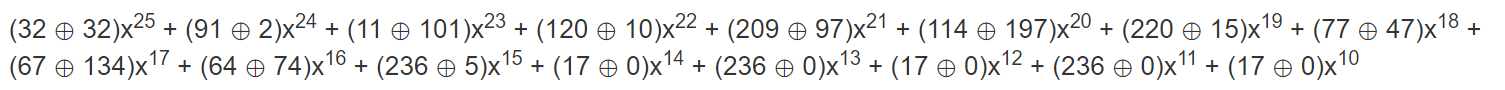
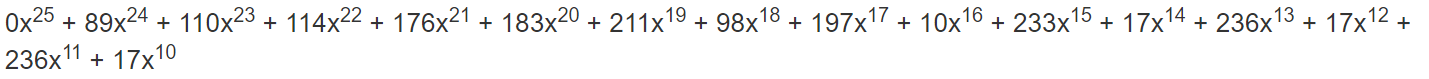
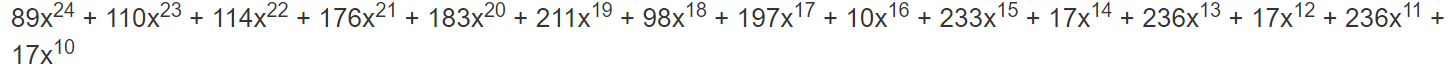
3. 将生成多项式乘上一步的XOR结果的前导项。注意，这里的生成多项式已经经过了和现在的信息多项式等指数的过程，所以最高次是24。

在这个例子中，前导项是89x^24,做乘法的时候，把数字用α表示比较简单，89又等于α^210(这个可以查表得)，所以

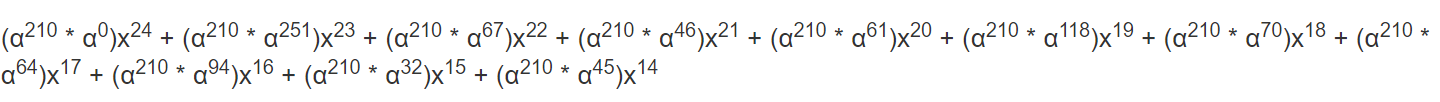
4.将上一步得到的式子继续重复类似步骤2的异或操作，这个操作之后，最前面那项（次数为24次的那项）又成功没有了。

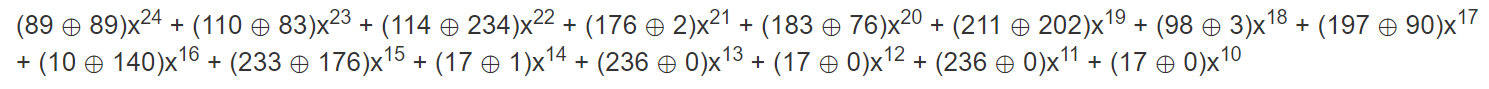
接下来这一步就可以想象啦，就是把61乘到原始的生成多项式上，把指数对好了的生成多项式和上一步得到的式子进行异或操作。

那么重复到什么时候好呢？从上面可以看出来，循环一次，就有一个消息多项式中的一项被消除，所以消息多项式有多少项，就进行多少次循环（这就好像除法进行到了最后一位）。上述例子循环16次后，就得到了下面这个式子（从这个式子中我们就可以看出来，刚开始的时候乘x^10有多明智，为什么是10而不是9或者8也从这里可以看出，因为生成多项式的最高次数是纠错码字的数目，一项项异或之后，最后的余数的位数和生成多项式的位数是相关的）