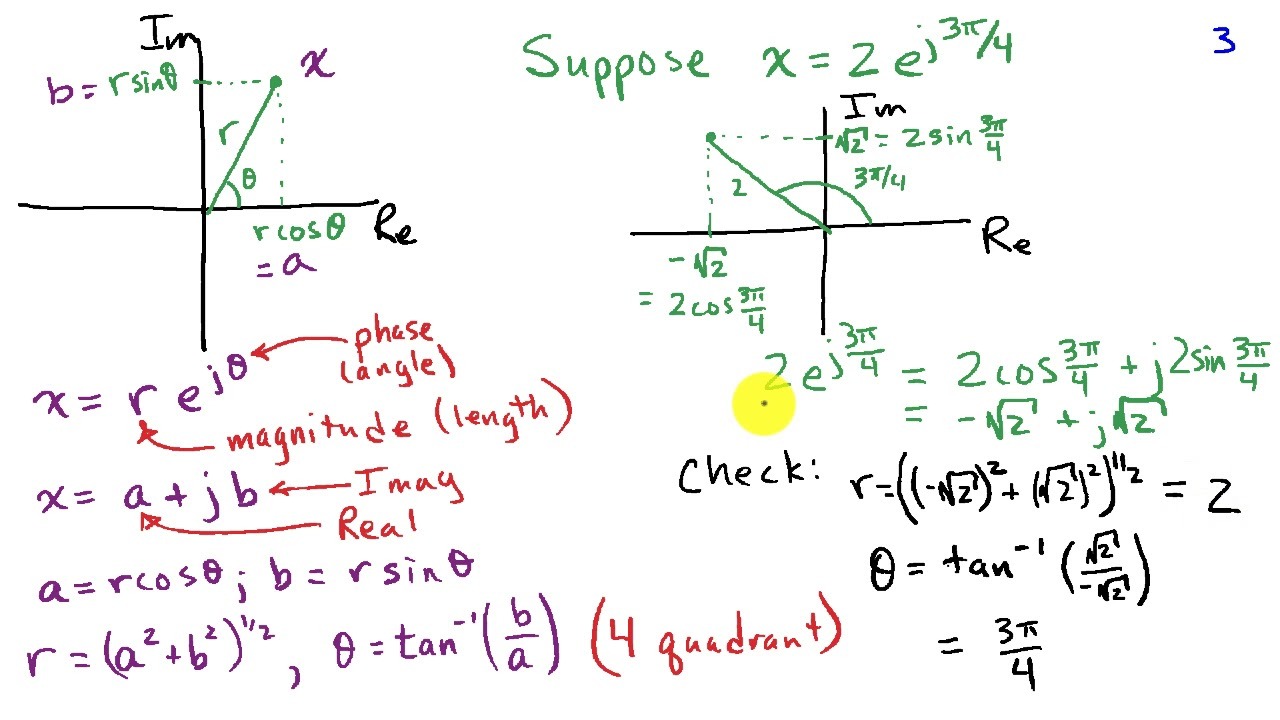
1.共轭复特征值
设
假设
所以,当
2. rotation-scaling matrix
假如
则有,
- A可以写成下面的旋转+缩放形式,
其中,
3. 矩阵的复特征值
首先我们假定下面的记号,
这里首先讨论的矩阵是
其中
为了证明矩阵
此外,我们假设复特征值
同时,
比较式(6)和(7),可以得到,
接下来我们计算
因为
因此
对于
对于上述矩阵
上述矩阵

设
假设
所以,当
假如
则有,
其中,

首先我们假定下面的记号,
这里首先讨论的矩阵是
其中
为了证明矩阵
此外,我们假设复特征值
同时,
比较式(6)和(7),可以得到,
接下来我们计算
因为
因此
对于
对于上述矩阵
上述矩阵

本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.mzph.cn/news/507723.shtml
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!