1 sigmoid函数
sigmoid函数是一个在生物学中常见的S型函数，也称为S型生长曲线。
sigmoid函数由下列公式定义:
σ(x)=11+e−x(1)\sigma(x) = \frac{1}{1 + e^{-x}} \tag1σ(x)=1+e−x1(1)
sigmoid函数的级数表示：
σ(x)=12+14x−148x3+1480x5−1780640x7+311451520x9−691319334400x11+O(x12)(2)\sigma(x) = \frac{1}{2} + \frac{1}{4}x - \frac{1}{48}x^3 + \frac{1}{480}x^5 - \frac{17}{80640}x^7 + \frac{31}{1451520}x^9 - \frac{691}{319334400}x^{11} + O(x^{12}) \tag2σ(x)=21+41x−481x3+4801x5−8064017x7+145152031x9−319334400691x11+O(x12)(2)
计算结果如下：
| xxx | σ(x)\sigma(x)σ(x) | xxx | σ(x)\sigma(x)σ(x) | xxx | σ(x)\sigma(x)σ(x) |
|---|---|---|---|---|---|
| -8 | 0.00033535 | -7 | 0.00091108 | -6 | 0.0024726 |
| -5 | 0.0066930 | -4 | 0.017986 | -3 | 0.047425 |
| -2 | 0.11920 | -1 | 0.26894 | 0 | 0.5 |
| 1 | 0.73105 | 2 | 0.88082 | 3 | 0.95256 |
| 4 | 0.98203 | 5 | 0.99330 | 6 | 0.99751 |
| 7 | 0.99910 | 8 | 0.99970 |
该函数的曲线如下：
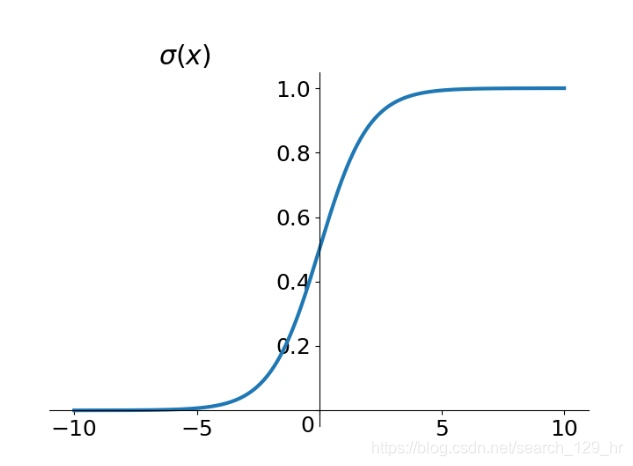
在信息科学中，由于其单增以及反函数单增等性质，sigmoid函数常被用作神经网络的激活函数，将变量映射到0,1之间。与之类似的还有softplus和softmax等函数。
函数具有以下几个特点：
- 值域在0和1之间
- 函数具有非常好的对称性
- 函数对输入超过一定范围就会不敏感，在趋于正无穷或负无穷时，函数趋近平滑状态
但该函数有以下几个缺点：
- 激活函数计算量大，反向传播求误差梯度时，求导涉及除法
- 反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练
应用：在二分类任务中，采用sigmoid的输出的是事件概率，也就是当输出满足某一概率条件将其划分正类。
其对x的导数可以用自身表示：
σ′(x)=e−x(1+e−x)2=σ(x)(1−σ(x))(3)\sigma'(x) = \frac{e^{-x}}{(1 + e^{-x})^2} = \sigma(x)(1 - \sigma(x)) \tag3σ′(x)=(1+e−x)2e−x=σ(x)(1−σ(x))(3)
2 softplus函数
该函数的数学表达式为：
ζ(x)=ln(1+ex)(4)\zeta(x) = \ln(1+e^{x}) \tag4ζ(x)=ln(1+ex)(4)
值域为(0,+∞)(0, +\infty)(0,+∞)，其函数图像为：
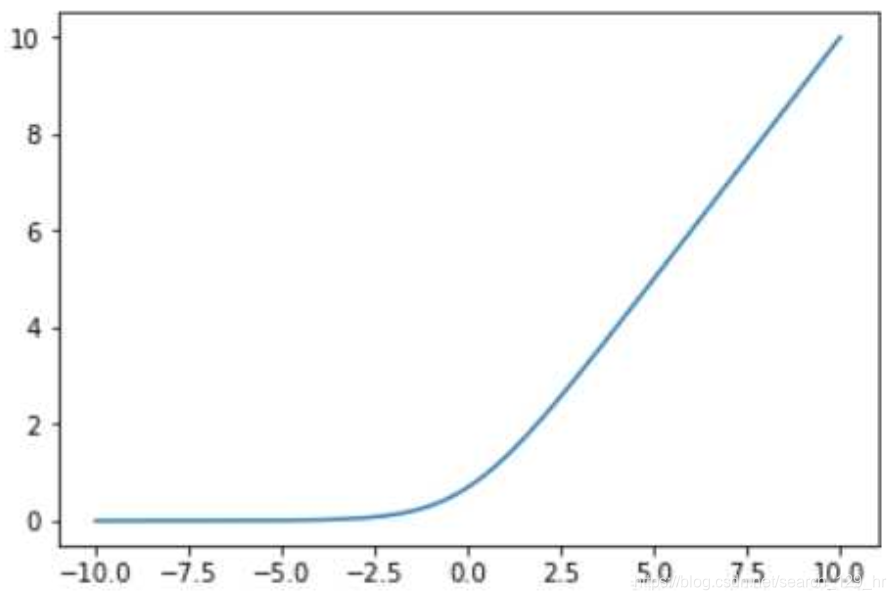
softplus函数与ReLU函数对比如下：
- softplus函数与ReLU函数接近，但比较平滑；
- 同ReLU一样是单边抑制,有宽广的接受域(0,+∞)(0, +\infty)(0,+∞)；
- softplus函数指数运算及对数运算，计算量大导致不太被人使用；
- 从一些人的使用经验来看(Glorot et al.(2011a))，softplus函数效果也并不比ReLU好。
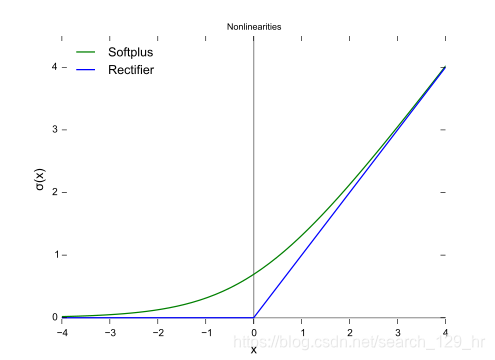
softplus的导数恰好是sigmoid函数.
softplus可以看作是ReLu的平滑。根据神经科学家的相关研究，softplus和ReLu与脑神经元激活频率函数有神似的地方。也就是说，相比于早期的激活函数，softplus和ReLu更加接近脑神经元的激活模型，而神经网络正是基于脑神经科学发展而来，这两个激活函数的应用促成了神经网络研究的新浪潮。
3 tanh函数
tanh是双曲函数中的一个，tanh()为双曲正切。在数学中，双曲正切“tanh”是由基本双曲函数双曲正弦和双曲余弦推导而来。
tanhx=sinhxcoshx=ex−e−xex+e−x\tanh x = \frac{\sinh x}{\cosh x} = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}tanhx=coshxsinhx=ex+e−xex−e−x
其曲线如下图所示：
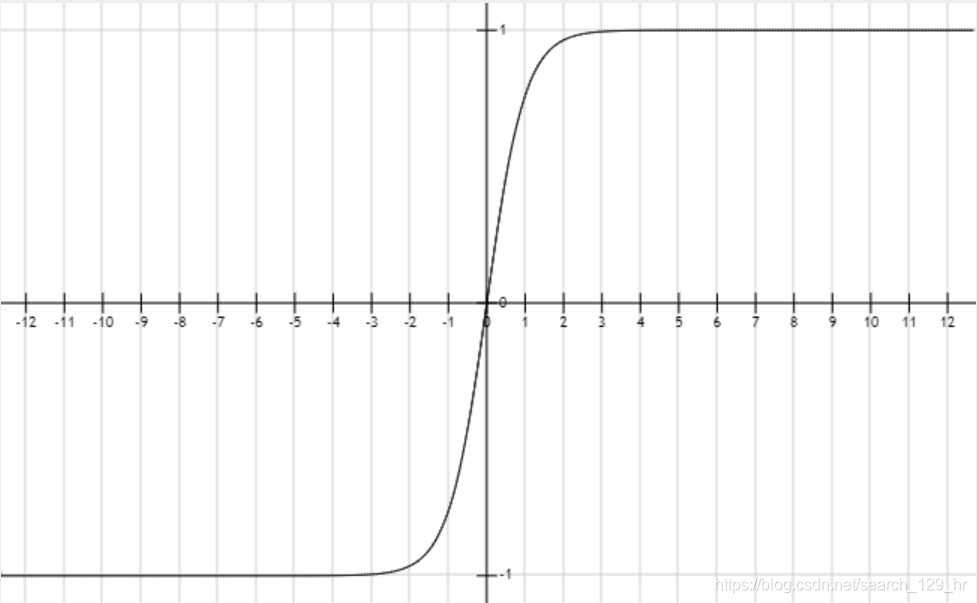
其导数为：
tanh′x=1−(ex−e−x)2(ex+e−x)2=1−tanh2x\tanh' x = 1- \frac{(e^{x} - e^{-x})^2}{(e^{x} + e^{-x})^2} = 1- \tanh^2xtanh′x=1−(ex+e−x)2(ex−e−x)2=1−tanh2x
其曲线如下图所示：
4 sigmoid函数σ(x)\sigma(x)σ(x)和softplus函数ζ(x)\zeta(x)ζ(x)一些重要性质
这些重要性质非常有用，需要背下来：
σ(x)=11+e−x=exex+1\sigma(x) = \frac{1}{1+e^{-x}} = \frac{e^x}{e^x + 1}σ(x)=1+e−x1=ex+1ex
ddxσ(x)=σ(x)(1−σ(x))\frac{d}{dx}\sigma(x) = \sigma(x)(1-\sigma(x))dxdσ(x)=σ(x)(1−σ(x))
1−σ(x)=σ(−x)1 - \sigma(x) = \sigma(-x)1−σ(x)=σ(−x)
logσ(x)=−ζ(−x)\log \sigma(x) = -\zeta(-x)logσ(x)=−ζ(−x)
ddxζ(x)=σ(x)\frac{d}{dx}\zeta(x) = \sigma(x)dxdζ(x)=σ(x)
∀x∈(0,1),σ−1(x)=log(x1−x)\forall x \in (0,1), \sigma^{-1}(x) = \log(\frac{x}{1-x})∀x∈(0,1),σ−1(x)=log(1−xx)
∀x>0,ζ−1(x)=log(ex−1)\forall x > 0, \zeta^{-1}(x) = \log(e^{x} - 1)∀x>0,ζ−1(x)=log(ex−1)
ζ(x)=∫−∞xσ(y)dy\zeta(x) = \int_{-\infty}^{x}\sigma(y)dyζ(x)=∫−∞xσ(y)dy
ζ(x)−ζ(−x)=x\zeta(x) - \zeta(-x) = xζ(x)−ζ(−x)=x
