许多简单的概率分布在机器学习的众多领域中都非常有用，这个内容将分为两个部分来说明，第一个部分介绍伯努利分布、二项式分布、多项式分布及范畴分布，第二个部分介绍高斯分布、指数分布、Laplace分布、Dirac分布、经验分布及混合分布。

伯努利(Bernoulli)分布

伯努利分布是一种离散分布，有两种可能的结果：

• 1表示成功，出现的概率为$p$(其中$0<p<1$)。
• 0表示失败，出现的概率为$q=1-p$。

这种分布在机器学习中很有用，比如正面或反面，成功或失败，有缺陷或没有缺陷，病人康复或未康复。
可以用数学描述为：随机变量$x$只取0和1两个值，其概率为：

• $P(x=1)=p$, $P(x=0)=1-p=q$

数学期望和方差计算如下：

• $E(x)=1\ast p+0\ast q=p$
• $E(x^2)=1^2\ast p+0^2\ast q=p$
• $D(x)=E(x^2)-[E(x){]}^2=p-p^2=p(1-p)=pq$

二项式(Binomial)分布

在$n$次独立重复的伯努利试验中，设每次试验成功的概率为$p$。用$x$表示$n$重伯努利试验中成功的次数，则$x$取值为{0,1,…,n}\{0, 1, \dots, n\}{0,1,…,n}中的一个。
对每一个$k(0\le k\le n)$，事件{x=k}\{x=k\}{x=k}表示“$n$次试验成功恰好发生$k$次”，随机变量$x$的离散概率分布即为二项分布（Binomial Distribution）。
典型例子为：扔硬币，硬币正面朝上概率为$p$, 重复扔$n$次硬币，$k$次为正面的概率即为一个二项分布概率。
用概率表示如下：

• $P(x=k)=\frac{n!}{k!(n-k)!}{p}^k(1-p{)}^{n-k}$

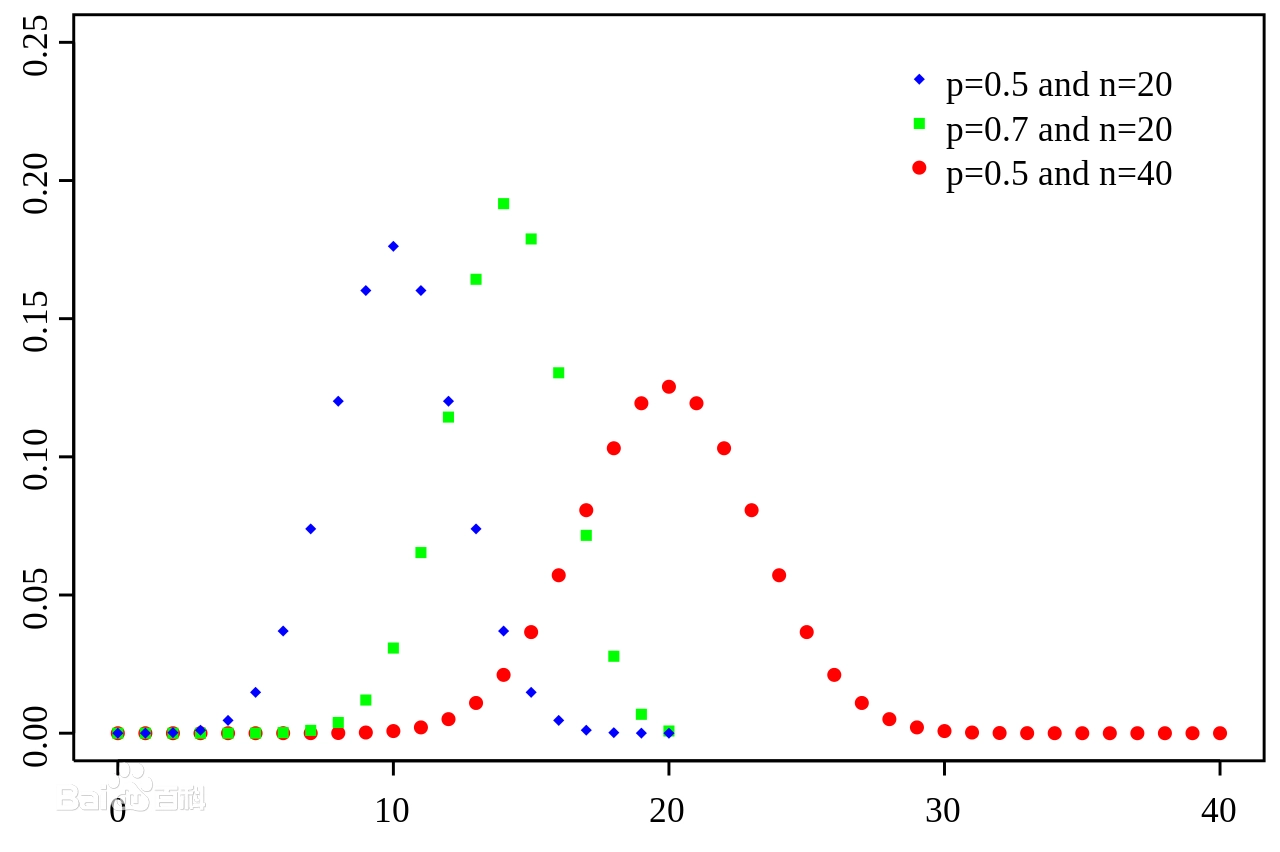
下图为不同参数下的二项式分布的图形：

多项式(Multinomial)分布

多项式分布是二项式分布的推广。将二项式分布推广至多种状态，就得到了多项式分布。举例说明如下：

• 二项式分布：扔硬币，硬币正面朝上概率为$p$, 重复扔$n$次硬币，$k$次为正面的概率。
• 多项式分布：扔骰子，不同于扔硬币，骰子有6个面对应6个不同的点数，这样单次每个点数朝上的概率都是$\frac{1}{6}$（对应$p_1$~$p_6$，它们的值不一定都是$\frac{1}{6}$，只要和为1且互斥即可，比如一个形状不规则的骰子），重复扔$n$次，如果问有$k$次都是点数6朝上的概率。

更一般化的描述如下：投掷$n$次骰子，这个骰子共有6种结果输出，1点出现概率为$p_1$，2点出现概率$p_2$，$\dots$；多项式分布给出了在$n$次试验中，骰子1点出现$k_1$次，2点出现$k_2$次，3点出现$k_3$次，…，6点出现$k_6$次。这个结果组合的概率为:
$f(k_1,k_2,\dots ,k_6;n,p_1,p_2,\dots ,p_6)$
$=P(x_1=k_1,x_2=k_2,\dots ,x_6=k_6)$
$=\frac{n!}{k_1!k_2!\dots k_6!}{p}_1^{k_1}{p}_2^{k_2}\dots p_6^{k_6}$,
约束条件为${\sum }_{i=1}^6{k}_i=n$.
为了更加简化，用$\Gamma$函数来表示：
$f(k_1,k_2,\dots ,k_6;n,p_1,p_2,\dots ,p_6)$
$=\frac{\Gamma ({\sum }_{i=1}^6{k}_i+1)}{{\prod }_{i=1}^6\Gamma (k_i+1)}{\prod }_{i=1}^6{p}_i^{k_i}$.
【例题-1】同时投掷5枚骰子，投掷出2个一点，2个二点，1个三点的概率是多大？
【解答】
$x_1$～$x_6$表示6个点的出现次数之和为$n=5$，利用多项式分布组合概率公式有：
$P(x_1=2,x_2=2,x_3=1,x_4=0,x_5=0,x_6=0)$
$=\frac{5!}{2!2!1!0!0!0!}(\frac{1}{6}{)}^2(\frac{1}{6}{)}^2(\frac{1}{6}{)}^1(\frac{1}{6}{)}^0(\frac{1}{6}{)}^0(\frac{1}{6}{)}^0$
$=\frac{5}{1296}$
【例题-2】同时投掷5枚骰子，出现两对点数一样的概率是多少？
【解答】
在【例题-1】的基础之上，需要考虑$x_1$~$x_6$，其中2个取2，1个取1有多少种？

$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$
2	2	1	0	0	0
2	0	2	1	0	0
$\dots$	$\dots$	$\dots$	$\dots$	$\dots$	$\dots$

先从6个里面选择2个取2，再从4个里面选出1个取1，总共有$C_6^2{C}_4^1=60$种。
出现两对点数一样的概率为$\frac{5\ast 60}{1296}$ = $\frac{25}{108}$。

范畴(Categorical)分布

范畴分布又称为Multinoulli分布、类别分布，它是多项式分布的一个特例。
抛一次骰子，第$x_k$面朝上的概率，这是Categorical分布。

小结：几种分布的关系

• 将一个小球放入两个桶，令变量 $x$ 为第一个桶里面有的小球个数，那么只有 0 个或者 1 个，服从伯努利分布；
• 将 $n$个小球放入两个桶，令变量 $x$ 为第一个桶里面的小球个数，那么最少可能有 0 个，最多可能有 $n$个，服从二项分布；
• 将一个小球放入 $k$个桶，令变量 x={x1,x2,…,xk}x = \{x_1, x_2, \dots, x_k\}x={x1​,x2​,…,xk​} 为$k$个桶内的小球个数，$x$是一个One-hot形式的向量，因为这个小球只能在一个桶里面，服从Categorical分布；
• 将 $n$个小球放入 $k$个桶，令变量 x={x1,x2,…,xk}x = \{x_1, x_2, \dots, x_k\}x={x1​,x2​,…,xk​} 为$k$个桶内的小球个数，$x$是一个向量，元素和为 $n$，服从多项分布。