Tikhonov regularization terms https://blog.csdn.net/jiejinquanil/article/details/50411617
本文是对博客https://baijiahao.baidu.com/s?id=1710942953471566583&wfr=spider&for=pc的重写。

1 简介

本文是对发表于计算机视觉和模式识别领域的顶级会议 ICCV 2021 的论文“ Orthogonal Jacobian Regularization for Unsupervised Disentanglement in Image Generation（用于无监督图像生成解耦的正交雅可比正则化）”的解读。

该论文由哈尔滨工业大学与好未来合作，针对图像生成中无监督解耦问题，提出了一种正交雅可比正则化（Orthogonal Jacobian Regularization, OroJaR）用于学习解耦的生成模型。OroJaR 通过约束输入各维在输出引起的变化之间的正交特性来实现模型的解耦，并使用输出对输入的雅可比矩阵表示这种变化。与之前的方法相比，OroJaR 可以应用于模型的多层，并以整体方式对输出进行约束，使得其可以更好的解耦空间相关的变化。

论文链接：https://arxiv.org/abs/2108.07668
代码地址：https://github.com/csyxwei/OroJaR

2 研究背景

近年来，无监督解耦学习受到了广泛的关注，不仅因为其对理解生成模型的重要性，也因为其对其他计算机视觉任务也有所帮助，如可控图像生成、图像编辑等。对于一个解耦的特征，其各维控制了输出中不相关的变化，从给定的数据集中无监督学习到解耦的特征仍是当前人工智能领域的一个重要挑战。

现有的无监督解耦方法主要基于两种主流的生成模型：变分自编码器（Variational Autoencoder, VAE）和生成式对抗网络（Generative Adversarial Networks, GAN）。基于 VAE 的方法如 -VAE [ 1 ] ，FactorVAE [ 2 ] 等主要通过约束隐变量之间的独立性来实现解耦，但受限于 VAE，这些方法生成图像的质量往往有限。随着 GAN 在图像生成领域取得的成功，许多基于 GAN 的无监督解耦方法被提出。SeFa [ 3 ] 通过对 pretrain 的 GAN 的第一层全连接层参数分解得到一系列解耦的隐空间方向向量。但 SeFa 只能作用于第一层且是后处理的方式，限制了其解耦性能。Hessian Penalty [ 4 ] 通过约束输出对输入的 Hessian 矩阵是对角的来实现解耦。但其使用 max 函数将约束从标量函数推广到向量函数，独立的约束输出的各个值使得其不能很好的解耦一些空间相关的变化（如，形状、大小、旋转等）。

受上述方法的启发，论文提出了一个用于无监督图像生成解耦的正交雅可比正则化（OroJaR），用于更好的解耦生成模型。

3 方法介绍

3.1 正交雅可比正则化 ( OroJaR )

令$G:X=G(\mathbf{z})$是一个生成模型，其中$\mathbf{z}=[z_1,\dots ,z_i,\dots ,z_m{]}^T\in \mathbb{R}$是输入向量，$z_i$表示输入的第$i$维。$\mathbf{x}$是网络的输出，$x_d=G_d(\mathbf{z})$进一步用于表示$G$的第$d$层的输出。
论文基于一个非常直观的想法：当改变输入的其中一维时，其在输出中引起的变化应该与其他维引起的变化独立（不相关），即$z_i$和$z_j$在输出中引起的变化是独立的。在论文中，作者使用雅可比向量$\frac{\partial G_d}{\partial z_i}$表示输入第$i$维在输出中引起的变化，同时为了实现解耦，作者约束输入各维对应的雅可比向量相互正交，
$$[\frac{\partial G_d}{\partial z_i}{]}^T\frac{\partial G_d}{\partial z_j}=0.\text{\hspace{1em}(1)}$$
两个向量的正交也意味着它们是不相关的，即输入各维所引起的变化是独立的。考虑所有输入维度，作者提出了正交雅可比正则化（OroJaR），来帮助模型学习到解耦的特征：
$$\mathcal{L}(G)=\sum _{d=1}^D||{\mathbf{J}}_d^T{\mathbf{J}}_d\circ (1-\mathbf{I})||=\sum _{d=1}^D\sum _{i=1}^m\sum _{j\ne i}|[\frac{\partial G_d}{\partial z_i}{]}^T\frac{\partial G_d}{\partial z_j}{|}^2,\text{\hspace{1em}(2)}$$
其中Jd={jd,1,…,jd,i,…,jd,m}\mathbf{J}_d = \{\mathbf{j}_{d, 1}, \dots, \mathbf{j}_{d, i}, \dots, \mathbf{j}_{d, m}\}Jd​={jd,1​,…,jd,i​,…,jd,m​}表示$G_d$对$z$输入的雅可比矩阵，$\circ$表示逐元素乘积。$\mathbf{I}$ 表示单位阵，$1$表示全 1 的矩阵。OroJaR 以整体方式对输出进行约束，而不是像 Hessian Penalty 一样独立的约束输出的每一个元素，这使得 OroJaR 可以更好的解耦复杂的、空间相关的变化。

3.2 近似训练加速

实际训练时，公式 (2)中雅可比矩阵的计算是非常耗时的。为了加速运算，作者基于Hutchinson近似[4,7]，将公式 (2)的计算重写为，
$$\mathcal{L}(G)=\sum _{d=1}^D\mathbf{V}\mathbf{a}{\mathbf{r}}_{\mathbf{v}}[{\mathbf{v}}^T({{\mathbf{j}}_{\mathbf{d}}}^T{\mathbf{j}}_{\mathbf{d}})\mathbf{v}]=\sum _{d=1}^D\mathbf{V}\mathbf{a}{\mathbf{r}}_{\mathbf{v}}[({\mathbf{j}}_{\mathbf{d}}\mathbf{v}{)}^T{\mathbf{j}}_{\mathbf{d}}\mathbf{v}],\text{\hspace{1em}(3)}$$
其中$\mathbf{v}$是Rademacher向量（每维为-1或1的概率为0.5），$\mathbf{V}\mathbf{a}{\mathbf{r}}_{\mathbf{v}}$表示方差计算。${\mathbf{j}}_{\mathbf{d}}\mathbf{v}$是$G_d$沿着$\mathbf{v}$方向的一阶导数乘上$|\mathbf{v}|$，其可以进一步使用一阶差分近似[8]估计得到：
$${\mathbf{j}}_{\mathbf{d}}\mathbf{v}=\frac{1}{ϵ}[G(\mathbf{z}+ϵ\mathbf{v})-G(\mathbf{z})],\text{\hspace{1em}(4)}$$

3.3 在GAN中的应用

OroJaR可以通过两种方式应用于GAN中，一种是在训练GAN时用作正则项，一种是用于寻找pretrain的GAN中一些解耦的方向向量。
GAN训练时，判别器$D$和生成器$G$迭代的使用${\mathcal{L}}_D$和${\mathcal{L}}_G$更新：
$${\mathcal{L}}_D={\mathbb{E}}_{\mathbf{x}}[f(D(\mathbf{x}))]+{\mathbb{E}}_{\mathbf{z}}[f(1-D(G(\mathbf{z})))],\text{\hspace{1em}(5)}$$
$${\mathcal{L}}_G={\mathbb{E}}_{\mathbf{z}}[f(1-D(G(\mathbf{z})))],\text{\hspace{1em}(6)}$$
其中$f(\cdot )$是某一个具体的GAN Loss。将OroJaR引入GAN的训练后，生成器的训练Loss调整为：
$${\mathcal{L}}_G^{oro}={\mathbb{E}}_{\mathbf{z}}[f(1-D(G(\mathbf{z})))]+\lambda {\mathbb{E}}_{\mathbf{z}}[{\mathcal{L}}_J(G(\mathbf{z}))],\text{\hspace{1em}(7)}$$
其中$\lambda$用于控制不同损失之间的权重。引入${\mathcal{L}}_J(G)$到GAN的训练中可以帮模型学习到解耦的特征，从而实现可控的图像生成。
OroJaR也可以用于发现pretrain的GAN的隐空间中可解释的方向。具体地，作者引入一个可学习的正交矩阵$\mathbf{A}\in {\mathbb{R}}^{m\times N}$，其中$N$是要学习的正交方向的个数，$m$是隐空间维度。$\mathbf{A}$的每列存储了要学习的正交方向。$A$的优化公式为：
$$A^{\ast }=\arg \underset{\mathbf{A}}{\min }{\mathbb{E}}_{\mathbf{z},{\omega }_i}{\mathcal{L}}_J(G(\mathbf{z}+\eta \mathbf{A}{\omega }_i)),\text{\hspace{1em}(8)}$$
其中ωi∈{0,1}N\omega_i \in \{0, 1\}^Nωi​∈{0,1}N是一个one-hot的向量，用于索引$\mathbf{A}$的某一列，$\eta$是一个标量用于控制$\mathbf{z}$应该沿着该方向移动多远。与公式 (7)不同的是，此时的OroJaR是对求的${\omega }_i$而不是$\mathbf{z}$。求得$\mathbf{A}$之后，就可以通过$G(\mathbf{z}+\eta \mathbf{A}{\omega }_i)$来对生成图像进行可控的编辑。

4 实验结果

论文使用了Edges+Shoes[9]、CLEVR[4]、Dsprites[10]等数据集对OroJaR进行了详细的定性和定量实验。

4.1 定性实验

作者首先在Edges+Shoes上进行了实验，该数据集是由5k张真实鞋子和5k张轮廓鞋子组成的真实数据集。从下图中可以看到，虽然没有其真实的变化因子，但SeFa[3]、Hessian Penalty[4]和OroJaR都学到了相同的变化，即鞋子的样式和形状，且论文提出的OroJaR具有更多样的形状变化。

下图给出了论文提出的OroJaR与对比方法在CLEVR-Complex数据集上的定性对比，该数据集包含2个物体的5个变化因子（x轴、y轴位置、形状、颜色、大小）。可以看到，SeFa[3]和Hessian Penalty[4]在改变一个物体的形状或颜色时另一个物体也会随之改变，而OroJaR可以独立的控制左右物体的形状和颜色，这说明OroJaR可以更好的解耦空间相关的变化。

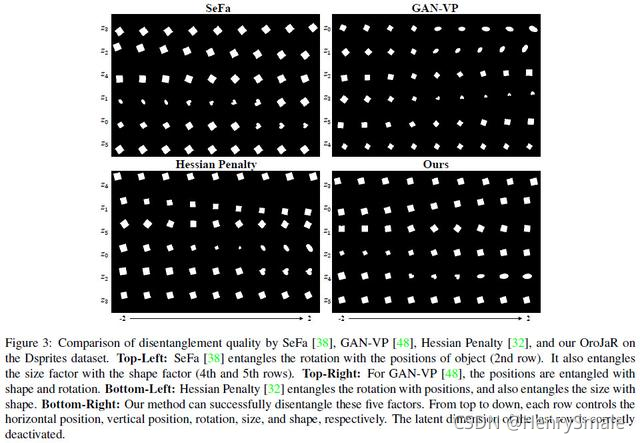
下图给出了OroJaR与对比方法在Dsprites数据集上的定性对比，该数据集是常用的解耦数据集，包含了1个物体的5个变化因子（x轴、y轴位置、形状、角度、大小）。可以看到与SeFa[3]和GAN-VP[5]和Hessian Penalty[4]相比，OroJaR可以更好地解耦5个变化，同时成功抑制多余的维度（第6行）。

如上文中提到的，OroJaR同样可以用于寻找pretrain的GAN的隐空间中一些有意义的方向向量，作者在ImageNet上pretrain的BigGAN[6]的Golden Retrievers和Churches两个类上进行了实验。实验结果如下图所示，可以看到，OroJaR可以成功找到一些有意义的控制，如旋转，缩放，颜色等。

更多详细的实验结果请见论文。

4.2 定量实验

下表给出了OroJaR在Edges+Shoes和CLEVR数据集上的定量对比实验，其中FID[12]用于衡量图像的生成质量，PPL[11]用于衡量模型隐空间的连续性，VP[5]用于衡量模型的解耦性能。可以看到，与SeFa[3]、InfoGAN[13]和Hessian Penalty[4]相比， OroJaR具有更高的VP指标，说明其更有利于模型的解耦。同时OroJaR也具有更低的PPL指标，这是因为OroJaR与StyleGAN2中提出的感知路径正则项具有相似的约束，从而实现了更低PPL。

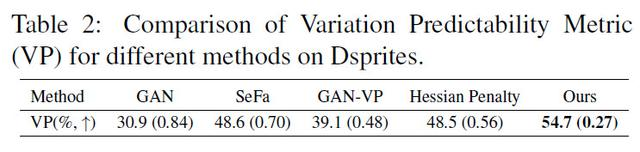
下表给出了OroJaR与对比方法在Dsprites上的VP指标对比，可以看到论文提出的OroJaR取得了更高的结果，说明了其在解耦上的优越性。

5 结语

论文提出了一种用于生成模型解耦的正交雅可比正则化 (OroJaR) ，其通过约束不同输入维度引起的输出变化（即雅可比向量）之间的正交性成功实现了模型的解耦。此外，OroJaR 可以应用于模型的多层，并以整体方式约束输出，使其可以有效地解耦空间相关的变化。

参考文献

[1] Irina Higgins, Loic Matthey, Arka Pal, Christopher Burgess, Xavier Glorot, Matthew Botvinick, Shakir Mohamed, and Alexander Lerchner. beta-vae: Learning basic visual concepts with a constrained variational framework. 2016.
[2] Hyunjik Kim and Andriy Mnih. Disentangling by factorising. In International Conference on Machine Learning, pages 2649–2658. PMLR, 2018.
[3] Yujun Shen and Bolei Zhou. Closed-form factorization of latent semantics in gans. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2021.
[4] William Peebles, John Peebles, Jun-Yan Zhu, Alexei A. Efros, and Antonio Torralba. The hessian penalty: A weak prior for unsupervised disentanglement. In Proceedings of the European Conference on Computer Vision, 2020
[5] Xinqi Zhu, Chang Xu, and Dacheng Tao. Learning disentangled representations with latent variation predictability. In Proceedings of the European Conference on Computer Vision, pages 684–700. Springer, 2020
[6] Andrew Brock, Jeff Donahue, and Karen Simonyan. Large scale gan training for high fidelity natural image synthesis. In International Conference on Learning Representations, 2018.
[7] Michael F Hutchinson. A stochastic estimator of the trace of the influence matrix for laplacian smoothing splines. Communications in Statistics-Simulation and Computation, 18(3):1059–1076, 1989.
[8] Clarence Hudson Richardson. An introduction to the calculus of finite differences. Van Nostrand, 1954.
[9] Aron Yu and Kristen Grauman. Fine-grained visual comparisons with local learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 192–199, 2014.
[10] Loic Matthey, Irina Higgins, Demis Hassabis, and Alexander Lerchner. dsprites:
Disentanglement testing sprites dataset. https://github.com/deepmind/dsprites-dataset/, 2017.
[11] Tero Karras, Samuli Laine, and Timo Aila. A style-based generator architecture for generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4401–4410, 2019.
[12] Martin Heusel, Hubert Ramsauer, Thomas Unterthiner, Bernhard Nessler, and Sepp Hochreiter. Gans trained by a two time-scale update rule converge to a local nash equilibrium. In Advances in Neural Information Processing Systems, pages 6629–6640, 2017.
[13] Xi Chen, Yan Duan, Rein Houthooft, John Schulman, Ilya Sutskever, and Pieter Abbeel. Infogan: interpretable representation learning by information maximizing generative adversarial nets. In Advances in Neural Information Processing Systems, 2016.