0 简介

网络的迅速发展带来了信息超载（information overload）问题。
解决信息超载问题一个非常有潜力的办法是推荐系统，它根据用户的信息需求、兴趣等，将用户感兴趣的信息、产品等推荐给用户。
推荐系统最典型应用领域是电子商务领域。同时学术界对推荐系统的研究热度一直很高，逐步形成了一门独立的学科。
一些名词能很好的刻画推荐系统，如千人千面、猜你喜欢等。

1 数据

推荐系统包括一些基础数据与附加信息。

1.1 基础数据

令用户数量为 $n$ , 商品数量为 $m$ . 用户对商品评分构成的矩阵 $R=(rij)n×m\mathbf{R} = (r_{ij})_{n \times m}$ . 如下表所示：
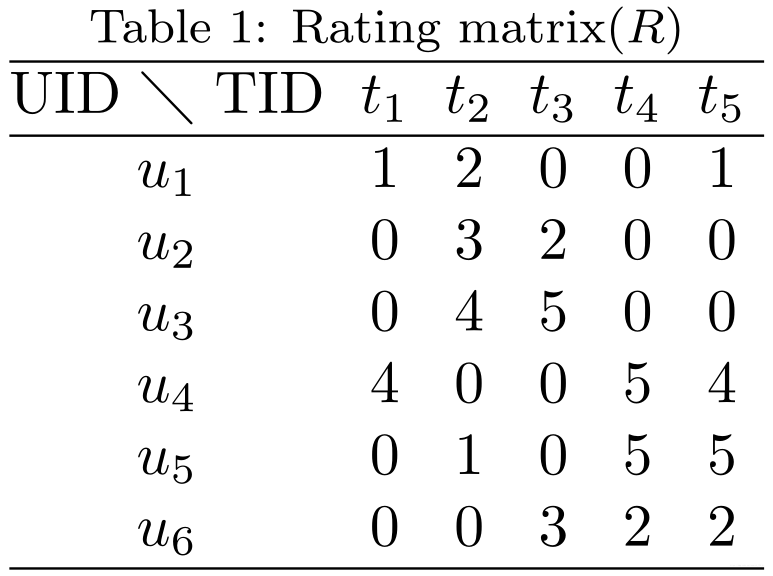
在这里插入图片描述
分两种情况讨论:

如果仅知道用户是否浏览过商品, $r_{ij}$ 的取值范围为 ${0, 1\}$ ， $R\mathbf{R}$ 表示浏览矩阵， $r_{ij} = 1$ 表示用户 $u_i$ 浏览过商品 $t_j$ ， $r_{ij} = 0$ 表示用户 $u_i$ 没有浏览过商品 $t_j$ ，这种评分也被称为隐式评分（implicit ratings）.
如果用户给购买过的商品进行评分， $R\mathbf{R}$ 表示评分矩阵， $r_{ij}$ 代表用户 $u_i$ 对商品 $t_j$ 的评分，一般的取值范围为 ${0, 1, 2, 3, 4, 5\}$ ,0分表示用户没有购买过商品，1分表示用户不喜欢该商品，5分表示用户特别喜欢该商品.

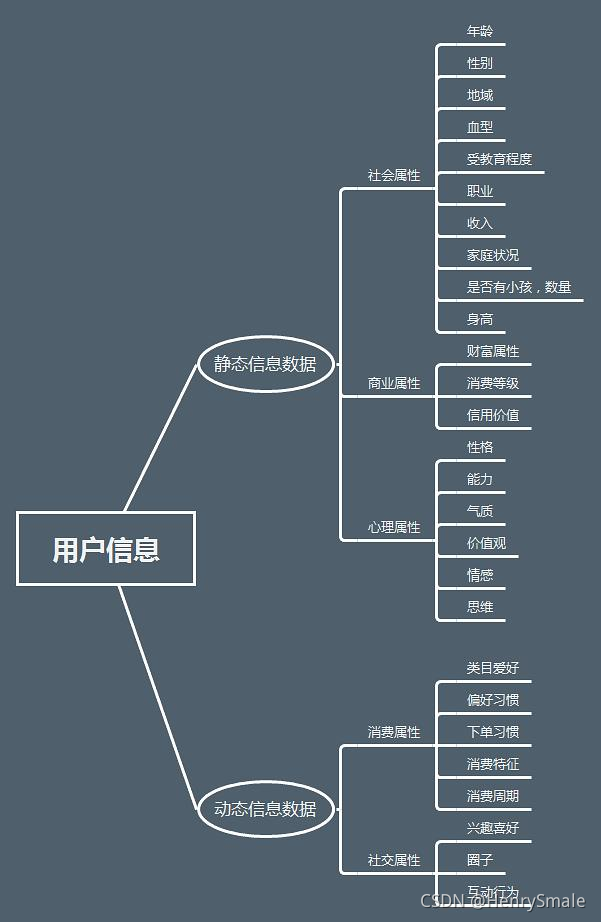
1.2 用户及商品信息

用户有自身信息, 如: 性别、国籍、信仰、年龄、职业等等.
商品有自身信息, 以电影为例, 包括: 出品时间、导演、主演、类型 (爱情片、动画片、喜剧片、悬疑片等，可多选)、片长等等.
以饭店为例, 有位置 (城市、街道)、营业时间、类别 (川菜、粤菜、鲁菜).

1.3 社交网络

用户与用户之间存在着信任关系（或称为好友），这样就构成了一个基于信任的社交网络，这些社交关系有利于给用户进行画像.
在这里插入图片描述

1.4 用户评论/点赞

用户不仅要给商品打分, 还会给用户/商品写一些评论或点赞. 这些评论或点赞可能比分数提供更丰富的语义信息.
在这里插入图片描述

1.5 其它信息

推荐系统应用广泛，如新闻、商品、音乐、视频等，都可以作为推荐的对象，针对不同应用场景，会收集很多相关信息，后续根据不同应用场景再补充。

2 问题

推荐系统的核心问题就是预测用户对商品的偏好。这种偏好可以用一个评分来表示，也可以用是否有浏览/购买的意愿来表示。针对具体的应用场景，需要说明输入、输出、优化目标、约束条件。

2.1 基于浏览矩阵的推荐

问题：浏览/购买预测
输入：训练矩阵 $Rt=(rijt)n×m\mathbf{R}^t = (r_{ij}^t)_{n \times m}$ ，所有评分矩阵 $R=(rij)n×m\mathbf{R} = (r_{ij})_{n \times m}$ .
输出：预测矩阵 $P=(pij)n×m\mathbf{P} = (p_{ij})_{n \times m}$ .
优化目标：最大化准确率
$max⁡acc(Rt,P,R)=∣{(i,j)∈R∣rijt=0,rij=1,pij=rij}∣∣{(i,j)∈R∣rijt=0,rij=1}∣\max acc(\mathbf{R}^t, \mathbf{P}, \mathbf{R}) = \frac{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} = 1, p_{ij} = r_{ij}\}|}{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} = 1\}|}$ .
其中：
1. $R\mathbf{R}$ 用于测试阶段评价推荐算法的准确率, 不能用于训练.
2. 完备矩阵 $R\mathbf{R}$ 在现实中并不存在.
3. 0 具有了有同解释 (语义), 在训练集 $Rt\mathbf{R}^t$ 中表示未知, 在预测矩阵 $P\mathbf{P}$ 中表示不喜欢或不购买, 在完备矩阵 $R\mathbf{R}$ 中既可能表示未知, 也可能表示不喜欢.

2.2 基于评分矩阵的预测

问题：评分预测
输入：训练矩阵 $Rt=(rijt)n×m\mathbf{R}^t = (r_{ij}^t)_{n \times m}$ ，所有评分矩阵 $R=(rij)n×m\mathbf{R} = (r_{ij})_{n \times m}$ .
输出：预测矩阵 $P=(pij)n×m\mathbf{P} = (p_{ij})_{n \times m}$ .
优化目标：

最小化平均绝对误差 (mean absolute error)
$min⁡mae(Rt,P,R)=Σ(i,j)∈{(i,j)∈R∣rijt=0,rij>0}∣pij−rij∣∣{(i,j)∈R∣rijt=0,rij>0}∣\min mae(\mathbf{R}^t, \mathbf{P}, \mathbf{R}) = \frac{\Sigma_{(i,j) \in \{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} > 0\}}|p_{ij} - r_{ij}|}{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} > 0\}|}$
最小化均方误差 (root mean square error)
$min⁡rsme(Rt,P,R)=Σ(i,j)∈{(i,j)∈R∣rijt=0,rij>0}(pij−rij)2∣{(i,j)∈R∣rijt=0,rij>0}∣\min rsme(\mathbf{R}^t, \mathbf{P}, \mathbf{R}) =\sqrt{ \frac{\Sigma_{(i,j) \in \{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} > 0\}}(p_{ij} - r_{ij})^2}{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} > 0\}|}}$

2.3 基于评分矩阵的推荐

问题：基于评分矩阵的推荐
输入：训练矩阵 $Rt=(rijt)n×m\mathbf{R}^t = (r_{ij}^t)_{n \times m}$ ，所有评分矩阵 $R=(rij)n×m\mathbf{R} = (r_{ij})_{n \times m}$ , 推荐阈值 $r_l$ .
输出：预测矩阵 $P=(pij)n×m\mathbf{P} = (p_{ij})_{n \times m}$ .
优化目标：最大化准确率
$max⁡acc(Rt,P,R)=∣{(i,j)∈R∣rijt=0,rij≥rl,pij≥rl}∣∣{(i,j)∈R∣rijt=0,rij≥rl}∣\max acc(\mathbf{R}^t, \mathbf{P}, \mathbf{R}) = \frac{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} \ge r_l, p_{ij} \ge r_{l}\}|}{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} \ge r_l\}|}$ .

2.4 交互推荐

在实际应用场景中，交互推荐是主流的推荐方式，推荐系统都会根据用户的选择优化推荐列表，也就是说用户这一轮的选择会影响下一轮的推荐列表。比如推荐系统一次给用户推荐20个商品，用户在本轮推荐中选择了商品1、3、5；这样的选择就会反馈给系统，系统根据用户的选择优化下一轮的推荐。交互式推荐用英文表达为 conversational recommendation.
场景描述:
对每个用户

登录系统;
do{获得系统推荐的一组项目 (固定为k个);用户在其中选择喜欢的所有项目;
}while(喜欢的项目为0个)

对系统

while(true){接收用户的选择，并将用户的选择写入灰列表(grey list);if(用户是不成熟用户){采用基于流行度的算法产生推荐列表;}else{采用基于矩阵分解的算法产生推荐列表;}
}

通过用户浏览/购买商品的数量达到某个阈值来表示用户的成熟度。如果达到某个阈值，则称该用户为成熟用户，否则为不成熟用户。
问题：交互式推荐
输入：训练矩阵 $Rt=(rijt)n×m\mathbf{R}^t = (r_{ij}^t)_{n \times m}$ ，所有评分矩阵 $R=(rij)n×m\mathbf{R} = (r_{ij})_{n \times m}$ .
输出：预测矩阵 $P=(pij)n×m\mathbf{P} = (p_{ij})_{n \times m}$ .
优化目标：最大化准确率
$max⁡acc(Rt,P,R)=∣{(i,j)∈R∣rijt=0,rij=1,pij=rij}∣∣{(i,j)∈R∣rijt=0,rij=1}∣\max acc(\mathbf{R}^t, \mathbf{P}, \mathbf{R}) = \frac{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} = 1, p_{ij} = r_{ij}\}|}{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} = 1\}|}$ .

2.5 三支推荐

推荐行为除了推荐和不推荐之外，实际上还存在着推广的行为，为了模拟这种行为，我们引入了三支推荐。
我们以下图为例来说明这个场景：
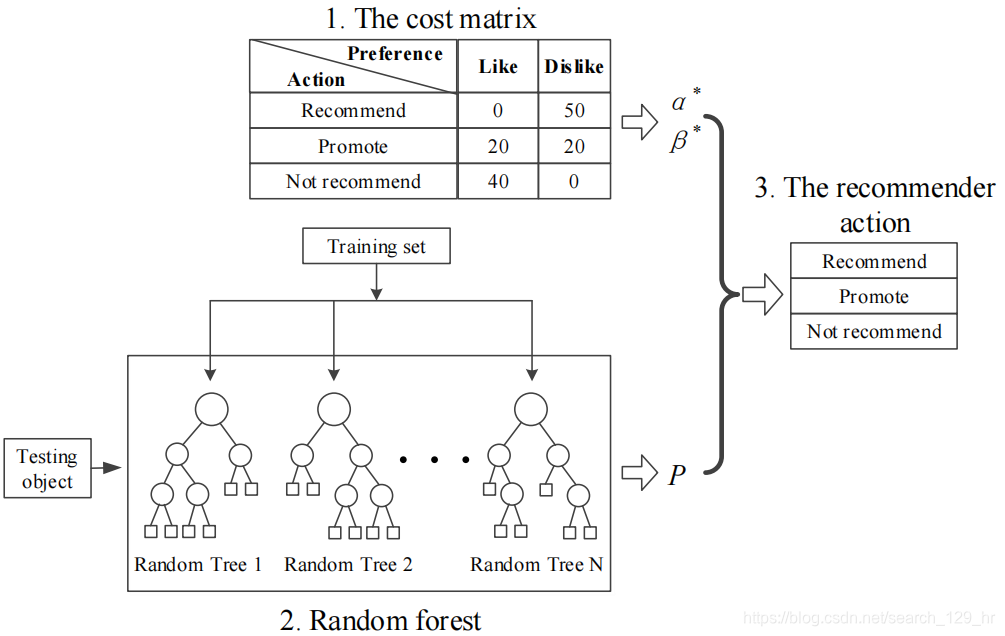
在这里插入图片描述
（1）我们设置了一个 $\times 2$ 的代价敏感矩阵，行表示系统对用户采取的行为，包括推荐(Recommend)、推广(Promote)、不推荐(Not recommend)，列表示用户的偏好，包括喜欢(Like)，不喜欢(Dislike)。根据三支决策理论，利用该代价矩阵可以计算出推荐阈值 $α∗\alpha^*$ 和 $β∗\beta^*$ ；
（2）利用随机森林我们可以预测出用户 $u_i$ 喜欢商品 $t_j$ 的程度，用概率 $p_{ij}$ 来表示；
（3）当 $pij>α∗p_{ij} \gt \alpha^*$ ，系统将推荐(Recommend)商品 $t_j$ 给用户 $u_i$ ；当 $pij<β∗p_{ij} \lt \beta^*$ ，系统将不推荐(Not recommend)商品 $t_j$ 给用户 $u_i$ ；当 $β∗≤pij≤α∗\beta^* \le p_{ij} \le \alpha^*$ ，系统将给用户 $u_i$ 分发优惠券进行推广(promote)商品 $t_j$ .
（4）为了描述下面的问题，我们需要用下面的公式进行映射：

根据偏好阈值 $r_l$ 将用户的评分映射为偏好:
$ψ(rij,rl)=1,当rij>rl\psi(r_{ij}, r_l) = 1, 当r_{ij} \gt r_l$ ;
$ψ(rij,rl)=2,当rij≤rl\psi(r_{ij}, r_l) = 2, 当r_{ij} \le r_l$ ;
将预测值映射为推荐(Recommend)、推广(Promote)、不推荐(Not recommend)
$ϕ(pij,α∗,β∗)=1,当pij>α∗\phi(p_{ij}, \alpha^*, \beta^*) = 1, 当p_{ij} \gt \alpha^*$ ;
$ϕ(pij,α∗,β∗)=2,当β∗≤pij≤α∗\phi(p_{ij}, \alpha^*, \beta^*) = 2, 当\beta^* \le p_{ij} \le \alpha^*$ ;
$ϕ(pij,α∗,β∗)=3,当pij<β∗\phi(p_{ij}, \alpha^*, \beta^*) = 3, 当p_{ij} \lt \beta^*$ .
问题：三支推荐
输入：训练矩阵 $Rt=(rijt)n×m\mathbf{R}^t = (r_{ij}^t)_{n \times m}$ ，所有评分矩阵 $R=(rij)n×m\mathbf{R} = (r_{ij})_{n \times m}$ , 代价矩阵 $(c_{kl})_{3 \times 2}$ .
输出：预测矩阵 $P=(pij)n×m\mathbf{P} = (p_{ij})_{n \times m}$ .
优化目标：最小化代价
$min⁡cost(Rt,P,R,C)=∑k∈{1,2,3},l∈{1,2}ckl×∣{(i,j)∈R∣ϕ(pij,α∗,β∗)=k,ψ(rij,rl)=l}∣∣{(i,j)∈R∣rijt=0,rij>0}∣\min cost(\mathbf{R}^t, \mathbf{P}, \mathbf{R}, C) = \frac{\sum_{k \in \{1,2,3\}, l \in \{1, 2\}} c_{kl} \times |\{(i, j) \in \mathbf{R} | \phi(p_{ij}, \alpha^*, \beta^*) = k, \psi(r_{ij}, r_l) = l\}|}{|\{(i, j) \in \mathbf{R} | r_{ij}^t = 0, r_{ij} > 0\}|}$ .

[1] Three-way recommender systems based on random forests

[2] Regression-based three-way recommendation

2.6 推荐系统的魔法边界

在很多时候，我们很想知道，给定一个推荐系统的数据集，它的精度上限（或者误差下限，为了更容易被记住，又取名为魔法边界）是多少，一旦知道了这个值，我们就可以确定算法到底还有多大的优化空间。换句话来说，就是数据质量本身决定了算法的精度上限，一旦数据集给定，这个魔法边界就确定了。
问题描述如下：

令 $O=(oij)n×m\mathbf{O} = (o_{ij})_{n \times m}$ 为一个理想的评分数据集(ideal rating data)，即假设用户在给商品评分的时候没有受到情绪波动、外界环境等因素影响，用户的偏好是恒定的；
令 $R=(rij)n×m\mathbf{R} = (r_{ij})_{n \times m}$ 为一个实际的评分数据集(real rating data), 用户在评分的时候受到情绪波动、外界环境等因素影响，会带入一些自然噪声(nature noise)；
令 $=|\{(i, j) \in \mathbf{R} | 1 \le i \le n, 1 \le j \le m, r_{ij} >0\}$ |；
基于MAE评价指标的魔法边界定义为： $\frac{|\mathbf{O} - \mathbf{R}|}{N}$
基于RSME评价指标的魔法边界定义为： $\frac{||\mathbf{O} - \mathbf{R}||_2}{N}$
我们认为魔法边界就是由于自然噪声引起的偏差。要估计这个魔法边界是一个很有挑战性的工作，因为实际环境中理想数据集 $O=(oij)n×m\mathbf{O} = (o_{ij})_{n \times m}$ 是采集不到的。
针对理想数据集的问题，有很多学者在这个方面做了一些尝试，目前主要有经验方法和理论方法两大类。
经验方法的学者通过采集同一用户对同一商品的多次评分，然后利用多次评分的平均来作为用户 $u_i$ 对商品 $t_j$ 的理想评分 $o_{ij}$ 。很显然，这种方法有很多缺陷，一方面同一用户对同一商品进行多次评分非常的无趣（boring），另一方面多次评分会带来新的噪声。
为了解决经验方法带来的问题，我们提出了一些理论方法（见已发表的论文)

[3] Magic barrier estimation models for recommended systems under normal distribution

我们做了如下假设：
$∣O−R∣N≤min⁡∣P−R∣N\frac{|\mathbf{O} - \mathbf{R}|}{N} \le \min \frac{|\mathbf{P} - \mathbf{R}|}{N}$
或
$∣∣O−R∣∣2N≤min⁡∣∣P−R∣∣2N\frac{||\mathbf{O} - \mathbf{R}||_2}{N} \le \min \frac{||\mathbf{P} - \mathbf{R}||_2}{N}$
该假设可以解读为：用户对商品的自然噪声所带来的偏差低于预测所带来的偏差。因为用户对商品的自然噪声是用户自己所导致的，而预测通常是利用其他用户对目标商品或者目标用户对其它商品的评分来估计目标用户对目标商品的评分，所以我们又可以解读为用户自身比别人更了解自己。

3 我们的工作

3.1 三支推荐

基于随机森林的三支推荐(Three-way recommender systems based on random forests)
三支回归推荐(Regression-based three-way recommendation)

3.2 交互推荐

交互场景下的二支推荐
交互场景下的三支推荐

3.3 魔法边界估计

基于高斯假设的估计(Magic barrier estimation models for recommended systems under normal distribution)
基于混合高斯(MoG)的估计
基于混合指数分布(MoEP)的估计

3.4 提高效率的推荐

- M-Distance
-多通道特征向量(MCFV）

3.5 可解释性推荐

矩阵分解： $R\mathbf{R}$ 由两个子矩阵 $X\mathbf{X}$ 和 $Y\mathbf{Y}$ 来表达，即 $R=XY\mathbf{R} = \mathbf{X}\mathbf{Y}$ . 其中向量 $x_i$ 表示用户 $u_i$ 的特征向量，向量 $y_j$ 表示商品 $t_j$ 的特征向量；
可解释性矩阵分解：当用户 $u_i$ 偏好于商品 $t_j$ 时，两者具有强相关性，其用户特征向量 $x_i$ 与商品特征向量 $y_j$ 在潜在空间上应互相接近,即 $∥xi−yj∥→0\|x_i -y_j \| \rightarrow 0$ 。

参考文献

[1] 张恒汝，闵帆，Three-way recommender systems based on random forests, Knowledge-Based Systems, 2016, 91: 275-286.
[2] 张恒汝，闵帆，石兵，Regression-based three-way recommendation，Information Sciences, 2017, 378, 444-461.
[3] 张恒汝, 闵帆等. Magic barrier estimation models for recommended systems under normal distribution, Applied Intelligence, 2018: 1-8.