1 摘要
最近的研究表明,推荐系统是脆弱的,攻击者很容易将精心设计的恶意配置文件注入系统,从而导致有偏见的推荐。我们不能否认这些数据的合理性,因此建立一个强大的推荐系统势在必行。对抗性训练已被广泛研究以获得可靠的建议。然而,传统的对抗训练给参数(输入)增加了小的扰动,这不符合推荐系统中的中毒机制。因此,对于非常擅长学习现有数据的实用模型,它的表现并不好。为了解决上述限制,我们提出了对抗性中毒训练(APT)。它通过注入虚假用户(ERM 用户)来模拟中毒过程,这些虚假用户致力于最小化经验风险以构建一个强大的系统。此外,为了生成 ERM 用户,我们探索了一种近似方法来估计每个假用户对经验风险的影响。尽管“以火取胜”的策略似乎违反直觉,但我们从理论上证明了所提出的 APT 可以提高中毒鲁棒性的上限。此外,我们提供了第一个理论证明,即对抗性训练对增强推荐稳健性具有积极影响。通过对四个真实世界数据集进行五次中毒攻击的广泛实验,结果表明 APT 的鲁棒性改进显着优于基线。值得一提的是,APT 在大多数情况下也提高了模型泛化能力。
2 预备知识
2.1 矩阵分解
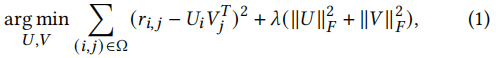
问:矩阵分解为什么不能进行精确分解?也就是R=UVR = UVR=UV,而不是R≈UVR \approx UVR≈UV。
答:从欠定方程、正定方程、超定方程角度考虑,由于评分矩阵上需要拟合的点比变量多,通过最小二乘法进行误差最小拟合。
问:为什么需要正则项?
答:为了防止过拟合。
问:为什么正则项必须是二范数?
答:一范数和二范数,还有其它的都可以作为正则项,推荐去看B站上的浙江大学胡浩基老师的《机器学习》的视频,里面有理论推导。
2.2 针对推荐系统的对抗训练
对抗训练向模型参数(或输入)添加扰动以迫使推荐系统适应这种噪声并学习扰动的非鲁棒性特征,从而增强面对对抗性攻击的鲁棒性。
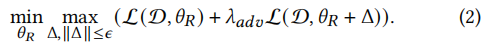
Δ\DeltaΔ是专门用于破坏推荐的附加扰动,ϵ>0\epsilon > 0ϵ>0限制扰动的幅度,λadv\lambda_{adv}λadv控制扰动的影响,D\mathcal{D}D、θR\theta_RθR和L\mathcal{L}L分别是推荐系统的数据集、参数和训练损失。
简而言之,对抗训练在推荐者和攻击对手之间进行零和博弈,并在博弈中寻求鲁棒模型。
问:公式(2)里面为什么有min\minmin,还有max\maxmax?
答:这个公式很有意思,可以分为两个步骤来理解,第一步是在已经训练好的模型(即固定参数θR\theta_RθR),攻击者通过加入扰动Δ\DeltaΔ使得模型的误差最大,这样可以保证攻击的效果最佳;第二步是利用已经污染后的数据集进行重新训练模型,也就是改变θR\theta_RθR,如果是矩阵分解,就是重新计算新的子矩阵UUU和VVV,使得损失最小。
2.3 威胁模型
攻击目标。根据攻击者的意图,他们可以设计各种攻击,包括提升攻击、降级攻击和可用性攻击[22]。提升攻击(降级攻击)通常旨在增加(降低)目标项目的受欢迎程度(例如,提高(降低)项目在基于排名的模型上的推荐排名 [24])。对于可用性攻击,攻击者希望最大化推荐误差以最终使模型无用。我们不能删除现有的评分,因此降级攻击可以通过增加非目标项目的受欢迎程度来实现,直到目标项目不在用户的推荐列表中[42],这在某种意义上相当于提升攻击。此外,可用性攻击本质上是提升攻击和降级攻击的混合体。为简单起见,我们主要专注于防御提升攻击。
攻击能力。理论上,只要注入的假配置文件足够大,任何模型都是脆弱的。显然,模型的鲁棒性和攻击能力不能解耦。另外,注入过多的假用户操作难度大,难免会产生与正常用户不同的签名,导致被检测到。鉴于上述考虑,我们限制攻击者最多注册 𝑛′ 恶意用户,每个用户的评分上限为 𝑚′。
攻击知识。 我们考虑白盒攻击下的研究; 也就是说,攻击者可以掌握推荐系统的一切,包括使用的算法、具体的参数设置,甚至用户的历史行为。 尽管获取知识的挑战使得这种理想的攻击不如黑盒攻击实用,但我们工作的重点是防御。 白盒攻击为防御提供了最差的假设,也是评估推荐稳健性的最严格的测试,超越了黑盒攻击。
3 对抗性中毒训练
假设D={r1,…,rn}\mathcal{D}=\{r_1, \dots, r_n\}D={r1,…,rn}是可能被污染的数据集。D∗={r1∗,…,rn∗∗}\mathcal{D}^*=\{r_1^*, \dots, r_{n^*}^*\}D∗={r1∗,…,rn∗∗}是一组致力于最小化经验风险的 n∗n^*n∗假用户,那么对抗性中毒训练的框架定义如下: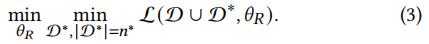
与公式(2)中描述的传统对抗训练相比,APT 的内在目标是最小化操作,APT 中使用的扰动是中毒用户,我们称之为 ERM 用户或防御用户。
问:又如何来理解公式(3)呢?
答:这个公式也可以分为两个步骤来理解,第一步是一批假用户进行评分得到数据集D∗D^*D∗,这个假用户的评分不能破坏原有评分的分布,也就是在原有参数θR\theta_RθR不变的情况下,损失最小;第二步是利用原有数据+新构造的数据集,重新训练新的参数θR\theta_RθR。
APT本质上模拟了对手的中毒过程,可以解决推荐中对抗训练的伪中毒问题。 当前的主要挑战是如何优化公式(3)的内在目标以产生ERM用户。 由于影响函数在决策预测中的应用 [19],我们通过估计每个用户对经验风险的影响来推导出一个近似求解器来生成 ERM 用户。
影响函数评估数据变化对决策的敏感性。 具体来说,对于训练集中的一个点zzz,我们对其添加一个小的扰动δ\deltaδ,使其成为z′=z+δz' = z + \deltaz′=z+δ。那么这个修改对测试点ztestz_{test}ztest的影响定义为:
Ipert,loss(z,δ):=−1n∇θL(ztest,θ^)THθ^−1∇z∇θL(z,θ^)δ\mathcal{I}_{pert, loss}(z, \delta) := -\frac{1}{n} \nabla_\theta \mathcal{L}(z_{test}, \hat{\theta})^T H_{\hat{\theta}}^{-1} \nabla_z \nabla_\theta \mathcal{L}(z, \hat{\theta}) \deltaIpert,loss(z,δ):=−n1∇θL(ztest,θ^)THθ^−1∇z∇θL(z,θ^)δ
符号说明:nnn是用户数,L\mathcal{L}L是公式一中的训练损失(training loss),HθH_\thetaHθ是训练损失的Hessian矩阵,∇\nabla∇一般表示梯度,在这里文章没有说明到底是什么。

影响向量I\mathcal{I}I为:

啃公式太吃力了,我们还是来看看算法流程吧:
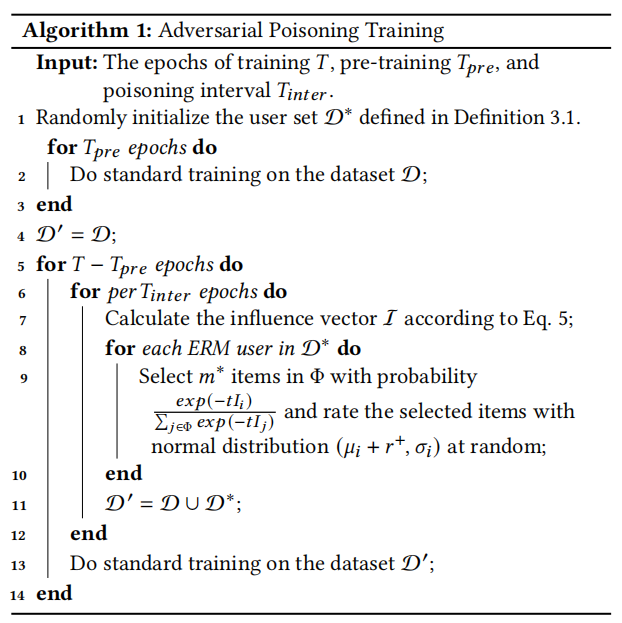
看了算法流程之后,我对这篇文章的工作有了一个大致的理解,分为五个步骤:
(1)随机添加一些用户构成假用户集D∗\mathcal{D}^*D∗;
(2)对原始数据集D\mathcal{D}D进行训练(矩阵分解);
(3)根据训练后的loss计算影响向量I\mathcal{I}I;
(4)以概率exp(−tIi)∑j∈Φexp(−tIj)\frac{exp(-tI_i)}{\sum_{j \in \Phi} exp(-tI_j)}∑j∈Φexp(−tIj)exp(−tIi)从项目集Φ\PhiΦ中选择m∗m^*m∗个项目,让假用户对这些项目进行评分,评分服从(μi+r+,σi)(\mu_i + r^+, \sigma_i)(μi+r+,σi);
(5)新的数据集为:D′=D∪D∗\mathcal{D}^{'} = \mathcal{D} \cup \mathcal{D}^*D′=D∪D∗,对新的数据集重新进行训练(矩阵分解)。
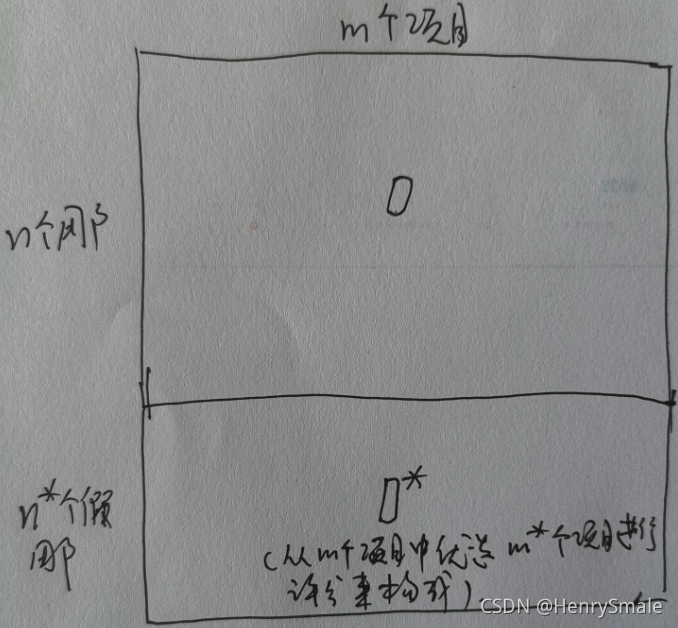
作者认为通过这种方式构建的新数据集可以有效的抵抗中毒攻击。
4 吐个槽,不对的地方请指正
看了这篇文章后,感觉有些关键的地方没有看懂:
(1)如何构建假用户集?
(2)选哪些项目来进行评分,也就是说具体的选择策略是什么?
(3)新的数据集为什么能抵抗中毒攻击?
个人觉得这篇文章有几个地方需要改进:
(1)符号系统较为凌乱,比如D∗\mathcal{D}^*D∗,一会儿指代假用户集,一会儿指代假用户评分后构建的数据集,可否增加一个符号系统;
(2)缺乏一个running example,也就是一个例子,通过这个例子可以帮助读者理解作者的具体做法。
)

)

)
)
)




)







