推荐系统–矩阵分解(1)
推荐系统–矩阵分解(2)
推荐系统–矩阵分解(3)
推荐系统–矩阵分解(4)
推荐系统–矩阵分解(5)
推荐系统–矩阵分解(6)

3 BiasSVD：考虑偏置

有一些用户会给出偏高的评分，有一些物品也会收到偏高的评分，比如电影观众为铁粉，一些受某时期某事件影响的电影。所以需要考虑偏置对评分的影响，其公式如下：
$$\begin{array}{r}L(\theta )=\underset{p_u,q_i}{\underbrace{\arg \min }}\sum _{u,i}{\left(r_{ui}-\mu -b_u-b_i-p_u^T{q}_i\right)}^2\\ +\lambda \left({\Vert p_u\Vert }_2^2+{\Vert q_i\Vert }_2^2+{\Vert b_u\Vert }_2^2+{\Vert b_i\Vert }_2^2\right)\end{array}\text{\hspace{1em}(4)}$$
符号说明：
用户的预测评分为：$\widehat{r_{ui}}=p_u^T{q}_i+\mu +b_u+b_i$；
偏差为：$e_{ui}=r_{ui}-\widehat{r_{ui}}$；
$\mu$：训练集中所有评分记录的全局平均数，表示了训练数据的总体评分情况，对于固定的数据集，它是一个常数；
$b_u$：用户$u$的偏置，独立于物品特征的因素，表示某一特定用户的打分习惯。例如，对于批判性用户对于自己的评分比较苛刻，倾向于打低分；而乐观型用户则打分比较保守，总体打分要偏高；
$b_i$：物品$i$的偏置，特立于用户兴趣的因素，表示某一特定物品得到的打分情况。以电影为例，好片获得的总体评分偏高，而烂片获得的评分普遍偏低，物品偏置捕获的就是这样的特征。
对公式（4）求偏导，理后可以得到迭代公式为：
$$\begin{array}{rl}{p}_{u,k}& =p_{u,k}+\eta \left(e_{ui}{q}_{k,i}-\lambda p_{u,k}\right)\\ q_{k,i}& =q_{k,i}+\eta \left(e_{ui}{p}_{u,k}-\lambda q_{i,k}\right)\\ b_u& =b_u+\eta \left(e_{ui}-\lambda b_u\right)\\ b_i& =b_i+\eta \left(e_{ui}-\lambda b_i\right)\end{array}\text{\hspace{1em}(5)}$$

4 SVD++：增加历史行为

通过观看B站上的视频，终于把SVD++核心思想搞清楚了：

• 它是来探索物品与物品之间关联关系的，比如对逃学威龙1评分高的人，可能也会给逃学威龙2高评分；
• 由于需要探索物品与物品之间的关联关系，可以使用显式反馈，也可以使用显式反馈+隐式反馈；
• 利用隐式反馈来探索物品与物品之间的关联关系，信息更加丰富：少数用户会主动点评电影或者美食，大多数用户只会浏览或者观看，也就是说显式反馈比隐式反馈少。

SVD++模型的步骤如下：

• 对于某一个用户$u$，它提供了反馈的物品集合定义为$N(u)$；
• 假设$j\in N(u)$，该物品$j$和预测物品$i$之间的关系为$w_{ij}$；
• 将这个关系作为预测评分的一个部分，则有如下公式：
  $$\begin{array}{r}\widehat{r_{ui}}=\mu +b_u+b_i+p_u^T{q}_i+\frac{1}{\sqrt{|N(u)|}}\sum _{j\in N(u)}{w}_{ij}\end{array}\text{\hspace{1em}(6)}$$
  引入$\frac{1}{\sqrt{|N(u)|}}$是为了消除不同$|N(u)|$个数引起的差异。
  $W$矩阵如下表所示：

	$t_1$	$t_2$	$t_3$	$t_4$
$t_1$	$w_{11}$	$w_{12}$	$w_{13}$	$w_{14}$
$t_2$	$w_{21}$	$w_{22}$	$w_{23}$	$w_{24}$
$t_3$	$w_{31}$	$w_{32}$	$w_{33}$	$w_{34}$
$t_4$	$w_{41}$	$w_{42}$	$w_{43}$	$w_{44}$

• $W$矩阵维度为$n\times n$，维度很大，我们对$W$进行矩阵分解后得到如下公式：
  $$\begin{array}{r}\widehat{r_{ui}}=\mu +b_u+b_i+p_u^T{q}_i+\frac{1}{\sqrt{|N(u)|}}{x}_u^T\sum _{j\in N(u)}{y}_j\end{array}\text{\hspace{1em}(7)}$$
  
• $x_u$表示用户的隐向量，可以用$p_u$替换，这样就减少了对$W$矩阵的分解，则上式可以表示为：
  $$\begin{array}{r}\widehat{r_{ui}}=\mu +b_u+b_i+p_u^T{q}_i+\frac{1}{\sqrt{|N(u)|}}{p}_u^T\sum _{j\in N(u)}{y}_j\\ =\mu +b_u+b_i+p_u^T\left(q_i+\frac{1}{\sqrt{|N(u)|}}\sum _{j\in N(u)}{y}_j\right)\end{array}\text{\hspace{1em}(10)}$$

其优化目标函数：
$$\begin{array}{r}L(\theta )=\underset{p_u,q_i}{\underbrace{\arg \min }}\sum _{u,i}{\left(r_{ui}-\mu -b_u-b_i-p_u^T{q}_i-p_u^T\frac{1}{\sqrt{|N(u)|}}\sum _{j\in N(u)}{y}_j\right)}^2\\ +\lambda \left({\Vert p_u\Vert }_2^2+{\Vert q_i\Vert }_2^2+{\Vert b_u\Vert }_2^2+{\Vert b_i\Vert }_2^2+\sum _{j\in N(u)}{\Vert y_j\Vert }_2^2\right)\end{array}\text{\hspace{1em}(11)}$$

对公式（11）求偏导，令$e_{ui}=r_{ui}-\widehat{r_{ui}}$，整理后可以得到迭代公式：
$$\begin{array}{r}{b}_u=b_u+\eta \cdot (e_{ui}-\lambda \cdot b_u)\\ b_i=b_i+\eta \cdot (e_{ui}-\lambda \cdot b_i)\\ p_u=p_u+\eta \cdot (e_{ui}\cdot q_i-\lambda \cdot p_u)\\ q_i=q_i+\eta \cdot (e_{ui}(p_u+\frac{1}{\sqrt{|N(u)|}}\sum _{j\in N(u)}{y}_j)-\lambda \cdot q_i)\\ y_j=y_j+\eta \cdot (e_{ui}\cdot \frac{1}{\sqrt{|N(u)|}}{q}_i-\lambda \cdot q_i)\end{array}\text{\hspace{1em}(12)}$$
参考的迭代公式如下：
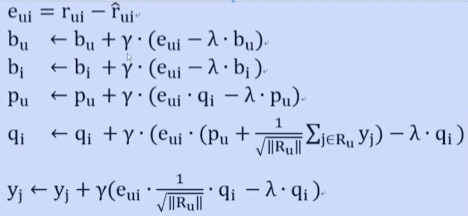