相关论文:
Secure Federated Matrix Factorization
论文源代码见: https://github.com/Di-Chai/FedMF
1 摘要
为了保护用户隐私和满足法律法规,联邦(机器)学习近年来获得了广泛的关注。 联邦学习的关键原则是在不需要知道每个用户的个人原始隐私数据的情况下训练机器学习模型。 在本文中,我们提出了联邦学习设置下的安全矩阵分解框架,称为 FedMF。 首先,我们设计了一个用户级分布式矩阵分解框架,当每个用户仅将梯度信息(而不是原始偏好数据)上传到服务器时,可以学习模型。 虽然梯度信息看起来很安全,但我们证明它仍然可能泄露用户的原始数据。 为此,我们使用同态加密来增强分布式矩阵分解框架。 我们实现了 FedMF 的原型并使用真实的电影评级数据集对其进行测试。 结果验证了 FedMF 的可行性。 我们还讨论了在实践中应用 FedMF 以进行未来研究的挑战。
2 问题引入


算法1描述了用户级别分布式矩阵分解的过程:

算法1所用到的公式如下:
minU,V1M(ri,j−⟨ui,vj⟩)2+λ∥U∥22+μ∥V∥22(2)\min _{U, V} \frac{1}{M}\left(r_{i, j}-\left\langle u_{i}, v_{j}\right\rangle\right)^{2}+\lambda\|U\|_{2}^{2}+\mu\|V\|_{2}^{2} \tag2U,VminM1(ri,j−⟨ui,vj⟩)2+λ∥U∥22+μ∥V∥22(2)
uit=uit−1−γ∇uiF(Ut−1,Vt−1)vit=vit−1−γ∇viF(Ut−1,Vt−1)(3)\begin{array}{l} u_{i}^{t}=u_{i}^{t-1}-\gamma \nabla_{u_{i}} F\left(U^{t-1}, V^{t-1}\right) \\ v_{i}^{t}=v_{i}^{t-1}-\gamma \nabla v_{i} F\left(U^{t-1}, V^{t-1}\right) \end{array} \tag3 uit=uit−1−γ∇uiF(Ut−1,Vt−1)vit=vit−1−γ∇viF(Ut−1,Vt−1)(3)
∇uiF(U,V)=−2∑j:(i,jvj(rij−⟨ui,vj⟩)+2λui∇vjF(U,V)=−2∑i:(i,jui(rij−⟨ui,vj⟩)+2λvj(4)\begin{array}{l} \nabla_{u_{i}} F(U, V)=-2 \sum_{j:(i, j} v_{j}\left(r_{i j}-\left\langle u_{i}, v_{j}\right\rangle\right)+2 \lambda u_{i} \\ \nabla_{v_{j}} F(U, V)=-2 \sum_{i:(i, j} u_{i}\left(r_{i j}-\left\langle u_{i}, v_{j}\right\rangle\right)+2 \lambda v_{j} \end{array} \tag4 ∇uiF(U,V)=−2∑j:(i,jvj(rij−⟨ui,vj⟩)+2λui∇vjF(U,V)=−2∑i:(i,jui(rij−⟨ui,vj⟩)+2λvj(4)
作者证明得到:如果获得用户传递的连续两次梯度,则可以推导出用户的评分信息。
rij=Gjktuikt+∑m=1Duimtvjmt(5)r_{i j}=\frac{G_{j k}^{t}}{u_{i k}^{t}}+\sum_{m=1}^{D} u_{i m}^{t} v_{j m}^{t} \tag5 rij=uiktGjkt+m=1∑Duimtvjmt(5)
3 解决方法
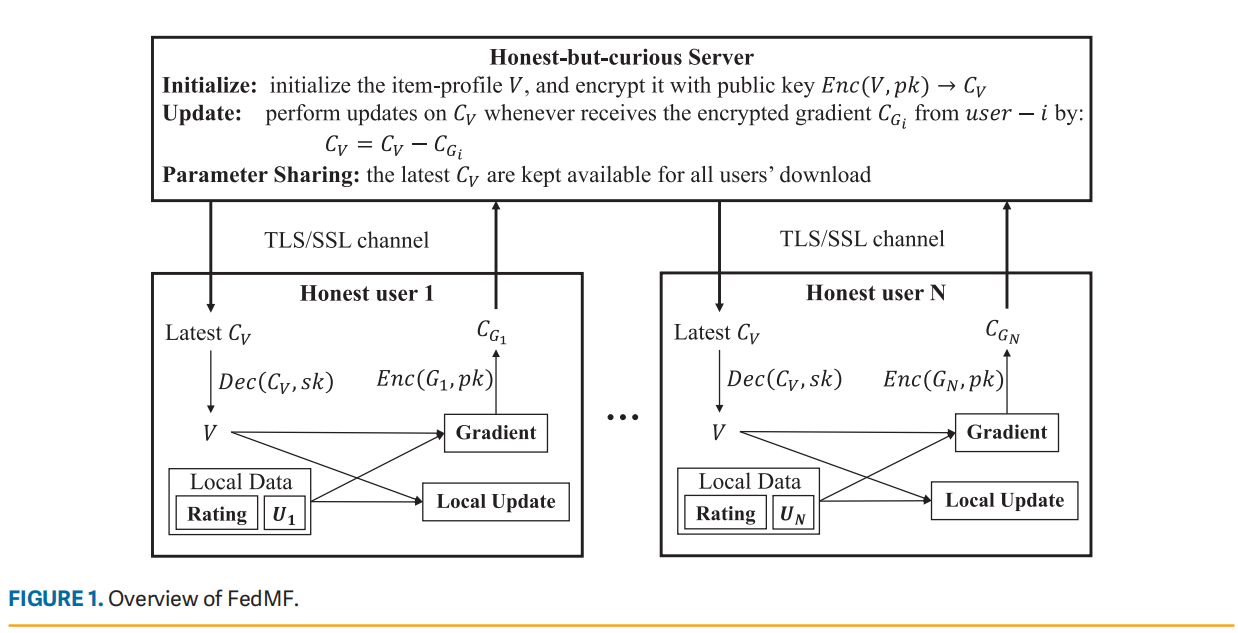
图 1 显示了方法的框架,称为 FedMF。 该框架涉及两种类型的参与者,服务器和用户。 正如前面“水平联邦学习”部分所说明的,假设服务器是诚实但好奇的,用户是诚实的,并且用户的隐私受到服务器的保护。
- 服务器使用公钥对项目配置文件 VVV 进行加密,得到密文 CVCVCV 。 从现在开始,为所有用户准备了最新的CVCVCV 。
- 每个用户从服务器下载最新的CVCVCV ,并使用秘钥解密,得到VVV的明文。 VVV 用于执行本地更新并计算梯度 GGG。然后,GGG 使用公钥加密,得到密文 CVCVCV 。 然后,建立一个 TLS/SSL 安全通道,通过这个安全通道将 CVCVCV 发送回服务器。
- 服务器收到用户的加密梯度后,使用这个更新item profile。
)

)

)

)

)

)




)
)


)