提要
平面内把一个图形沿着一定的方向移动一定的距离得到另一个图形,这种变换称为平移变换。根据需要,平移的对象可以是线段,直线,角,圆,整个图形等。平移只改变图形的位置,不改变图形的形状和大小。平移前后的线段,角,弧长,面积保持不变,平移前后的线段平行,对应点连线平行且相等,对应角的两边分别平行且方向一致,这种性质在解题中起着重要作用。平移的实质就是一种转化。通过平移,寻求已知条件与所求问题之间的关系,从而找到更为合理的解题之路。
知识全解
一.平移法的概念
利用平移变换及其性质解题的方法叫做平移法。平移法是分析和解决几何问题,函数图像问题的重要方法之一。若题设中有平行条件或委托中关于线段或角的已知条件位置分散,常可用平移变换将一部分条件转移到同一个三角形或平行四边形中。
理解平移应注意以下3点:1.平移是运动的一种形式,是图形变换的一种,这里所说的平移是指在同一平面内的图形变换;2.平移只改变图形的位置,不改变图形的形状和大小;3.平移是由平移的方向和距离决定的,平移的方向是图形上某一点到它对应点的方向,平移的距离是图形上某一点与它的对应点所连线段的长度;4.图形的平移实质上是将图形上所有点按同一方向移动同样的距离。
二.平面直角坐标系中的平移
(1)平面直角坐标系中直线的平移:直线y=kx+b(k≠0)平移前后系数k的值不变。直线向上,下平移m(m>0)个单位分别得y=kx+b+m,y=kx+b-m;向左,右平移m个单位分别得y=k(x+m)+b,y=k(x-m)+b。
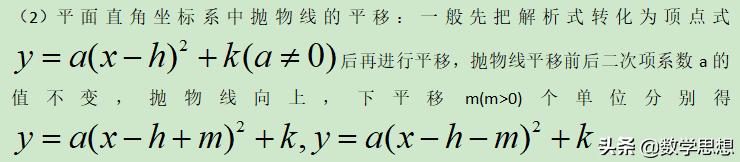
坐标系中图形的平移,实质上是点的平移。
学法指导
类型1 平面几何中的平移
例1 如图所示,梯形ABCD中,AD‖BC,∠B+∠C=90度,M,N分别是AD,BC的中点,求证:MN=(BC-AD)/2
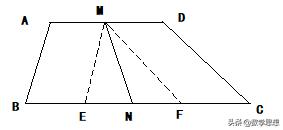
【解析】平移两腰,作ME‖AB交BC于E,MF‖CD交BC于F,则得到平行四边形ABEM,CDMF,直角三角形MEF,根据平行四边形的性质易得EF=BC-AD,又因为MN是Rt△MEF斜边上的中线,所有MN=1/2EF,即MN=(BC-AD)/2
【点评】本题经过平移使线段,角的位置发生变化,从而条件和结论互相靠拢,为解题创造了条件。
类型2 平面直角坐标系中的平移
例2 如图所示,在边长为1的小正方形网格中,△AOB的顶点均在格点上
(1)B点关于y轴的对称点坐标为__
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1
(3)在(2)的条件下,点A1的坐标为__
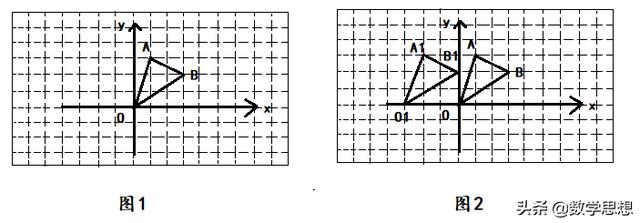
【解析】(1)由图1知,点B的坐标为(3,2),根据关于y轴对称的点的横坐标互为相反数,纵坐标相等,所有B点关于y轴对称的点的坐标应是(-3,2)
(2)可以由图1得出O,A,B三点的坐标为O(0,0),A(1,3),B(3,2),向左平移3个单位长度后得到对应三点的坐标分别为O1(-3,0),A1(-2,3),B1(0,2),在坐标系中描出这三点后再顺次连接即可;也可以根据平移的性质作出三角形△A1O1B1,如图2所示。
(3)点A1的坐标为(-2,3)
【点评】由平移方式求出三角形3个顶点的对应点的坐标,在坐标系中标出对应点,顺次连接即得平移后的图形。
链接中考
考点1 平移方法
例1 如图所示,在方格纸中,线段a,b,c,d的端点在格点上,通过平移其中两条线段,使得和第三条线段首尾相接组成三角形,则能组成三角形的不同平移方法有()
A.3种 B.6种 C.8种 D.12种
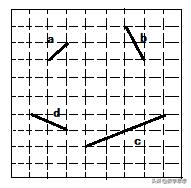
【解析】由图,根据勾股定理可得:a=√2,b=√5,c=2√5,d=√5。因为a+b
如下图所示,通过平移a,b,d其中两条线段,使得和第三条线段首尾相接组成三角形,能组成三角形的不同平移法有6种。

【点评】本题利用平移的知识解决问题,有利于创新能力的培养。
考点2 平移性质
例2 如图所示,四边形ABCD中,对角线AC,BD交于点O,且AC=BD,E,F分别是AB,CD的中点,连接EF分别交AC,BD于P,Q两点。求证:∠OPQ=∠OQP
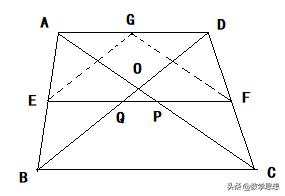
【解析】出现中点,故能想到添加中位线,达到平移角的目的。取AD的中点G,连接EF,FG,则∠OPQ=∠GFP,∠OQP=∠GEP
∵EG=1/2BD,GF=1/2AC,BD=AC
∴EG=GF
∴∠GFP=∠GEP
∴∠OPQ=∠OQP
【点评】本题还可以取BC的中点,利用平行线的性质(内错角相等)达到转化角的目的。
考点3 平移直线
例3 (1)直线y=2x+1向下平移2个单位后的表达式是__
(2)直线y=2x+1向右平移2个单位后的表达式是__
【解析】易知该直线与y轴的交点坐标为A(0,1),且根据一次函数性质,直线平移后比例系数k不变,仍是2,于是可设平移后的函数表达式为y=2x+b
(1)设平移后的函数表达式为y=2x+b。直线y=2x+1向下平移2个单位后,A点的坐标变为(0,-1),代入y=2x+b中,解得b=-1,此时函数表达式为y=2x-1。
(2)直线y=2x+1向右平移2个单位后,A点坐标变为(2,1),代入y=2x+b,解得b=-3,此时函数表达式为y=2x-3
【点评】直线的平移规律,可以借助直线上几个特殊点的坐标变化来找到。
考点4 平移抛物线

【解析】(1)令x=0,则y=c,故C(0,c)
∵OC的距离为3
∴|c|=3,即c=±3
∴C(0,3)或(0,-3)
(2)∵x1·x2<0,∴x1,x2异号
1.若C(0,3),即c=3
把C(0,3)代入y2=-3x+t,即0+t=3,即t=3
∴y2=-3x+3
把A(x1,0)代入y2=-3x+3,即-3x1+3=0,即x1=1
∴A(1,0)
∵x1,x2异号,x1=1>0,∴x2<0
∵|x1|+|x2|=4
∴1-x2=4
解得:x2=-3,则B(-3,0)
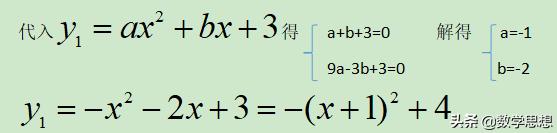
则当x≤1 时,y随x增大而增大
2. 若C(0,-3),即c=-3,把C(0,-3)代入y2=-3x+t,则
0+t=-3,即t=-3
∴y2=-3x-3
把A(x1,0)代入y2=-3x-3,则
-3x1-3=0,即x1=-1
∴A(-1,0)
∵x1,x2异号,x1=-1<0,∴x2>0
∵|x1|+|x2|=4
∴1+x2=4
解得:x2=3,则B(3,0)
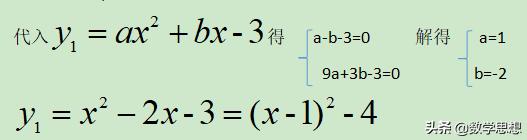
则当x≥1 时,y随x增大而增大
综上所述,若c=3,当y随x增大而增大时,x≤-1
若若c=-3,当y随x增大而增大时,x≥1

【点评】此题主要考查了二次函数综合,二次函数的平移以及二次函数增减性等知识,利用分类讨论得出n的取值范围是解题关键。



)




)



)
)

——Python语言基础_Python视频-51CTO学院...)



