Picture from Internet
DID是什么？
双重差分法(DID)又被称为“倍差法”，小名“差中差”，是种专门用于分析政策效果的计量方法。
我国最早引入DID方法对公共政策评估的权威文献是周黎安和陈烨(2005)，研究税费改革对农民收入增长的影响。由于税费改革政策为试点改革，最早从安徽省开始实施，紧接着推广到江苏、湖南、湖北的部分县进行试点，最终推广到全国各县市。该政策在试点实施的时候使得一部分城市受到影响，而其他部分城市没有受到影响或者影响很小，因此作者将该政策的实施视为自然实验，引入DID方法评估税收改革的效果。
DID被广泛应用的原因？
(1) 可以很大程度上避免内生性问题的困扰。内生性问题一般来源于：双向因果、遗漏变量、样本选择、动态面板、测量误差。政策相对于微观经济主体而言一般是外生的，因而不存在逆向因果问题。此外，使用固定效应估计一定程度上也缓解了遗漏变量偏误问题。
(2) 传统方法下评估政策效应，主要是通过设置一个政策发生与否的虚拟变量然后进行回归，相较而言，双重差分法的模型设置更加科学，能更加准确地估计出政策效应。
(3) 双重差分法的原理和模型设置很简单，容易理解和运用，并不像空间计量等方法一样让人望而生畏。
基准的DID模型设置如下：
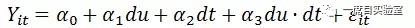
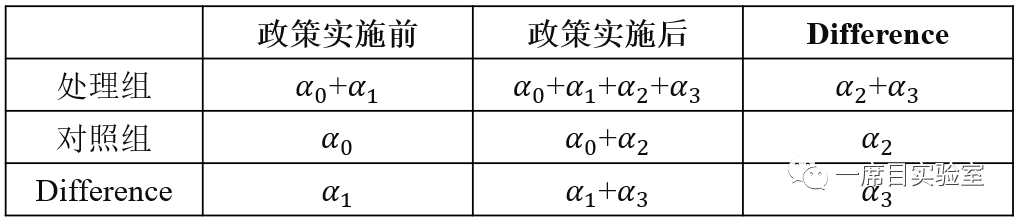
其中，du为分组虚拟变量，若个体i受政策实施的影响，则个体i属于处理组，对应的du取值为1，若个体i不受政策实施的影响，则个体i属于对照组，对应的du取值为0。dt为政策实施虚拟变量，政策实施之前dt取值为0，政策实施之后dt取值为1。du·dt为分组虚拟变量与政策实施虚拟变量的交互项，其系数反应了政策实施的净效应，这一点可以通过下表来体现。
Picture from Internet
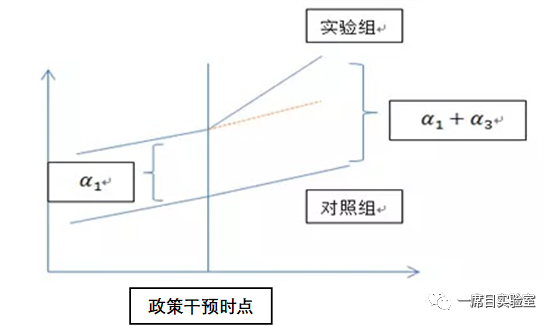
图中黄色的虚线表示的是假设政策未实施时，实验组的变化趋势，即实验组的反事实情况。该图也反映出了DID最为重要和关键的前提条件：平行趋势条件，即处理组和控制组在没有政策干预的情况下，结果效应的趋势是一样的，也可以说在政策干预之前，处理组和控制组的结果效应的趋势是一样的。当公共政策实施前的数据超过两期时，可以通过图形或安慰剂来检验处理组和控制组是否满足平行趋势。对于因“选择偏误”等原因导致的违背平行趋势条件的样本数据可以考虑通过 PSM-DID 方法或者DDD三重差分模型来测算，这个方法在国内评估政策效果时用得相对较多。
此外，为了得到经典双重差分方法的一致性估计量至少还需要满足以下两个条件：SUTVA条件，政策干预只影响处理组，不会对对照组产生交互影响，或者政策干预不会产生外溢效应；线性形式条件，潜在结果变量同处理变量和时间变量满足线性关系。
DID的稳健性检验：
稳健性检验考察的是评价方法和指标解释能力的强壮性，也就是当改变某些参数时，评价方法和指标是否仍然对评价结果保持一个比较一致、稳定的解释。通俗些，就是改变某个特定的参数，进行重复的实验，来观察实证结果是否随着参数设定的改变而发生变化。如果改变参数设定以后，结果发现符号和显著性发生了改变，说明不是稳健性的，需要寻找问题的所在。
DID的稳健性检验——必须证实所有效应确实是由政策实施所导致的。常用的稳健性检验有下面几种:
(1) 安慰剂检验。具体可以: a)选取政策实施之前的年份进行处理，比如原来的政策发生在2008年，研究区间为2007-2009年，这时可以将研究区间前移至2005-2007年,并假定政策实施年份为2006年，然后进行回归; b)选取已知的并不受政策实施影响的群组作为处理组进行回归。如果不同虚构方式下的DID估计量的回归结果依然显著，说明原来的估计结果很有可能出现了偏误。(2) 利用不同的对照组进行回归，看研究结论是否依然一致。(3) 选取一个完全不受政策干预影响的因素作为被解释变量进行回归，如果DID估计量的回归结果依然显著，说明原来的估计结果很有可能出现了偏误。要说明的是，如果回归结果显著，说明原结果是一定有问题的，而如果回归结果不显著，并不一定能表明原结果没问题。
参考文献:
[1] 陈林,伍海军. 国内双重差分法的研究现状与潜在问题[J].数量经济技术经济研究,2015,32(07):133-148.[2] 胡日东,林明裕. 双重差分方法的研究动态及其在公共政策评估中的应用[J].财经智库,2018,3(03):84-111+143-144.
撰文：文凌
编辑：文凌
往期推荐
行为研究前沿 | 医生提供在线医疗咨询和患者评论效价：准实验证据
行为研究前沿 | 金融可得性、金融市场参与和家庭资产选择
行为研究前沿 | 无人售货机补货员何时遵循算法的摆放策略？零售业现场实验
