背景

之前在一个项目中，涉及到了金额，协议组定的标准是按照分的单位进行传递的，但是交互上，web页面中为了更友好的体验，是使用的元作为单位的，这个时候就需要转换一下单位

本来是很简单的一个转化的需求，在和后端联调的时候发现，保存的时候返回了参数错误，原因就是由于js浮点数精度带来的影响，导致保存的时候保存的位数特别多。

之前的开发过程中，对这个不精确的问题只是了解，有问题了就parseInt一下，但没有去细想过要怎么解决，所以今天整理了一下之后分享一下，先了解下原因，再看下怎么解决和规避

问题

输入金额 0.55，我传递之后应该乘 100 后下发，正常来说应该传的是55，但是实际上，由于精度丢失，最后的结果如下图所示:

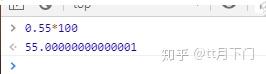
那追根溯源，到底为什么会产生精度丢失的问题呢？

计算机底层只有0 和 1， 所以所有的运算最后实际上都是二进制运算。十进制整数利用辗转相除的方法可以准确地转换为二进制数，但浮点数呢？

先看下面一张图，是关于IEEE 754标准（IEEE二进位浮点数算术标准（IEEE Standard for Floating-Point Arithmetic）的标准编号）：

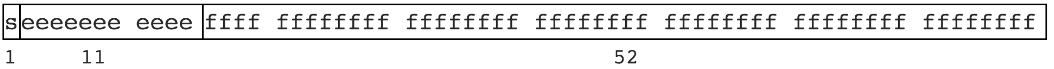
这个标准是JS的浮点数的实现标准，大概解释一下这张图就是：

• 第一位是符号位
• 中间11位代表的是指数位
• 最后的52位代表尾数位

也就是说，浮点数最终在运算的时候实际上是一个符合该标准的二进制数

我们可以看一个例子：

为了验证该例子，我们得先知道怎么将浮点数转换为二进制，整数我们可以用除2取余的方式，小数我们则可以用乘2取整的方式。

0.1转换为二进制：

• 0.1 * 2，值为0.2，小数部分0.2，整数部分0
• 0.2 * 2，值为0.4，小数部分0.4，整数部分0
• 0.4 * 2，值为0.8，小数部分0.8，整数部分0
• 0.8 * 2，值为1.6，小数部分0.6，整数部分1
• 0.6 * 2，值为1.2，小数部分0.2，整数部分1
• 0.2 * 2，值为0.4，小数部分0.4，整数部分0
• 从0.2开始循环

0.2转换为二进制：

• 可以直接参考上述，肯定最后也是一个循环的情况

所以最终我们能得到两个循环的二进制数：

0.1：0.0001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1001 1100 ...

0.2：0.0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 0011 ...

这两个的和的二进制就是：

sum：0.0100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 1100 ...

所以最终我们只能得到和的近似值（按照IEEE 754标准保留 52位，按 0舍1入 来取值）

利用按权相加法，sum的十进制数则为：

sum ≈ 0.30000000000000004

这个例子说明了什么？

说明JS浮点数精度的缺失实际上是因为浮点数的小数部分无法用二进制很精准的转换出来，而以近似值来进行运算的话，肯定就存在精度的问题

解决

了解了真相之后，我们可以怎么处理呢？

我的项目中是直接parseInt了一下，因为误差很小，可以忽略不计。

但后来想想不能这么就放过去了，这种一刀切的方法太暴力了，万一涉及到需要特别精确的场景，这种方法会有问题。

所以，最好的办法还是需要找方法提高精度，直接规避。

思路其实非常简单，既然浮点数的情况下会丢失精度，那我们所有运算的时候都先小浮点数转换为整数，等计算完之后，再按比例转换会浮点数，这样就避免了再二进制十进制转换的时候计算机的精度问题。

比如上面的加法的例子，我们定义一个工具函数add：

const 

现在我们再来看看结果：

但有个问题，我们之前还有个例子，0.55在乘的时候就会产生精度问题，所以这里我们再优化一下，把一个数变成整数，是不是也可以理解为将其变成字符串后把小数点去掉再转回数字，这样效果和相乘的效果不是一样的吗：

const 

这样就解决了。

当然，这只是考虑了最简单的情况，比如如果位数不同还要特殊处理下。不过只要思路有了，后续的就属于添砖加瓦了，考虑得很全面的话，可以考虑封装成一个库，这篇文章就权当抛砖引玉吧。