首先,做一个简短的开场白。
本贴主要是一个关于信号处理方面的学习笔记。主要目的有三,
- 作为研究笔记留存
- 分享我个人的理解
- 与专业人士进行意见交换
另外由于楼主不是教课员,因此无法保证算法分析以及个人理解的完全正确性,若本人对知识点的理解有不到位的地方望予以指正。
下面进入正题。
【概要】
数字滤波器主要分为【有限冲激响应系统】(FIR系统)以及【无限冲击响应系统】(IIR系统)。他们的优缺点如下表所示,根据数据精度需求的不同,应选用相匹配的系统进行滤波

下面通过具体的特性公式来理解。
【FIR系统】
一. 基础结构与特性方程:
FIR系统是有限冲激响应系统,与移动平均方法类似,
假设我们有一个有限冲激响应h[n],
h[n], n=0,1,...,M (h[n]=0, n<0, n>M)
为了进行滤波,对其进行卷积和运算,可得到以下输入与输出函数关系,

其结构图可以总结为下图,
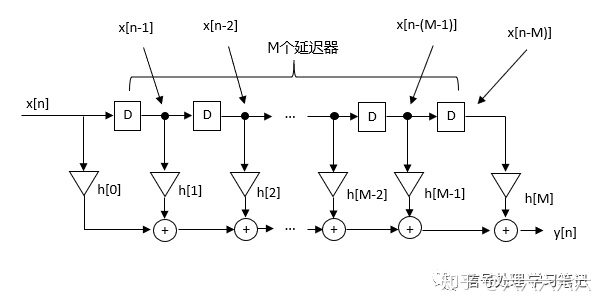
具备这种结构的数字系统我们就称其为FIR系统(FIR滤波器)。当然FIR滤波器的结构不止一种,以上这种结构叫做直接型FIR系统,其他的还有转置型FIR系统,以及转置型线性相位FIR系统。
通过差分方程与z变换公式(代换z=e^jΩ),我们可得到FIR滤波器的特性公式(推导过程在此省略,我们直接研究结果):
频率特性:
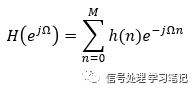
幅频特征:
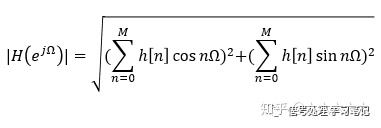
相频特征:
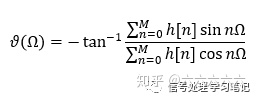
这之中,h[n]为冲击响应,考虑到冲激响应长度(M+1)的奇偶性,可划分分为以下4种类型。
(a)偶对称,冲激响应长度为奇数
(b)偶对称,冲激响应长度为偶数
(b)奇对称,冲激响应长度为奇数
(b)奇对称,冲激响应长度为偶数
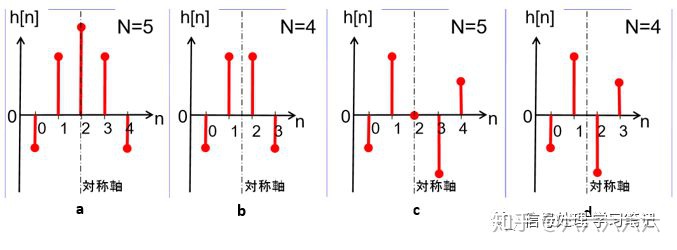
我们把冲激响应(a)带入上述特性公式中,
频率特性:
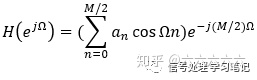
幅频特性:
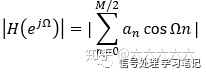
相频特性:
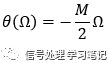
二. 理解分析:
**频率特性**
FIR系统的频率特性其实是由FIR系统的传递函数,通过带入z=e^jΩ所得。
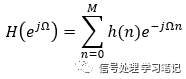
观察这个公式我们可以知道,FIR系统的频率特性,其实就是冲激响应h(n)的频率普,即DTFT(h(n))。
同时在FIR系统中,h(n)指的是系统函数(数字系统传递函数)的分子系数。使用Matlab设计FIR滤波器时,Matlab会根据我们设定的参数自动计算并返回这个值。
**幅频特性**
幅频特性指的是滤波器的衰减率。横坐标为频率,纵坐标为衰减率。
简单来说幅频特性反应的物理意义,就是一个原始波x(n)中所包含的各个频率成分,在滤波后还剩下的比例。
观察实际的幅频特性公式,我们发现衰减率的大小与频率的三角函数值相关。因此我们可以理解FIR系统的衰减率是其实是通过三角函数来近似实现的。当冲击响应h[n]的阶数M较低时,通过三角函数就很难再现出一条直线,特性曲线如图所示:
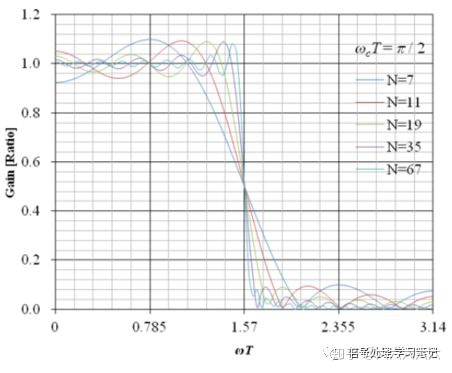
我们可以看到,通带衰减率为一个在1附近振荡的三角函数曲线,因此滤波后数据会产生失真。但是当h[n]的阶数足够大时,幅频特性会无限接近于1,从而近似的实现全域通过特性。但是由于FIR系统为有限长冲激响应,因此阻带无法接近于0,呈现如下图所示波纹。
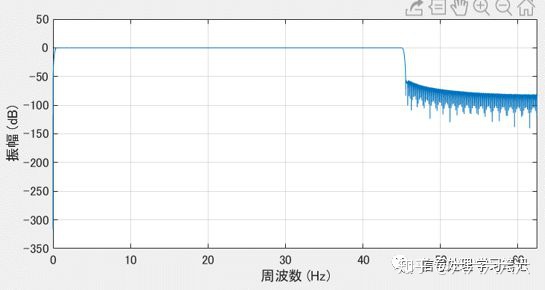
这里还有一个容许误差的概念,由于FIR系统只是通过三角函数近似的再现全域通过特性,因此通过控制阶数M使三角函数的振幅限制在一定范围之内,这个范围被称为容许误差,通过这种方法可以适当的减少滤波器阶数M,减少信号延迟。
**相频特性**
下面我们来聊聊相频特性。
首先什么是相频特性。简单来说就是指原始信号x(n)中所包含的各个频率成分,在滤波后所产生的延迟量。
当冲激响应h(n)为(a)时,我们可以得到相频特性方程为:
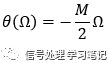
也就是说,FIR系统的相频特性曲线为一条与角频率相关的直线,我们称这种相频特性为线性相频特性或直线相频特性。
物理意义方面解释的话,就是说滤波后的各个不同频率成分产生时相互之间的延迟时间是呈线性分布的。

这种线性相位特性有什么好处呢?为什么是FIR系统的优点?
网上有一个简单易懂的例子,以音乐会为例子,有兴趣的可以参考看看。
出自:https://blog.csdn.net/deepdsp/article/details/6804888
**延迟**
最后我们聊聊延迟,在滤波系统中,有两个延迟的存在。
- 相位延迟
- 群延迟
相位延迟
首先相位延迟,指的就是上文所述的相频特性所产生的各个不同频率成分之间的延迟量。这个延迟若不是线性的,则会产生信号失真,对滤波结果的精度影响较大。
群延迟(group delay)
定义为入力波形与出力波形的相位差与角频率的微分。
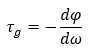
带入相频特性方程中,
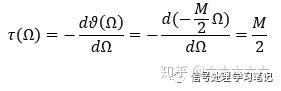
可以看出,当相频特性为线性时,群延迟为常数,滤波器阶数的一半。
那所以呢?会有什么影响?
其实很简单,从物理学角度来讲,群延迟其实就是波形整体向右平移了M/2 Point的距离。根据采样频率的不同,这M/2 Point可以是1s的数据量(采样频率100Hz),也有可能是0.1s的数据量(采样频率1000Hz)。
在offline分析中,这个延迟是可以通过去除对应数据量进行补偿的。但是另一方面,在online分析中,这个延迟往往会产生很大影响。如何去除这个相位延迟,工程上有很多补偿的方法(等我研究好了再分享),但是就FIR系统本身来说,这里就涉及到零相位的课题了。
返回FIR系统的算法结构图,我们可以看到通过延迟器后的数据都是x[n-1],也就是说现在时间点的数据,其实是过去M个时间点数据和对应冲激响应的卷积和。这个特性,被称为滤波器的因果特性。只有具备这种特性的滤波器,才可在online系统中使用。
举个栗子,当我们处于信号输出的开始点的时候,也即是说我们没有过去数据,这种时候我们是没有办法进行滤波的。这个就是群延迟以及相位延迟产生的原因。滤波器必须等到具备足够的数据之后,才可以开始工作。
套用一句经典的话,想要做到实时的零相位延迟,需要两个步骤:
1)move to another universe;
2)enjoy!!
出自:https://blog.csdn.net/csdn_kike/article/details/69061673
三. 验证
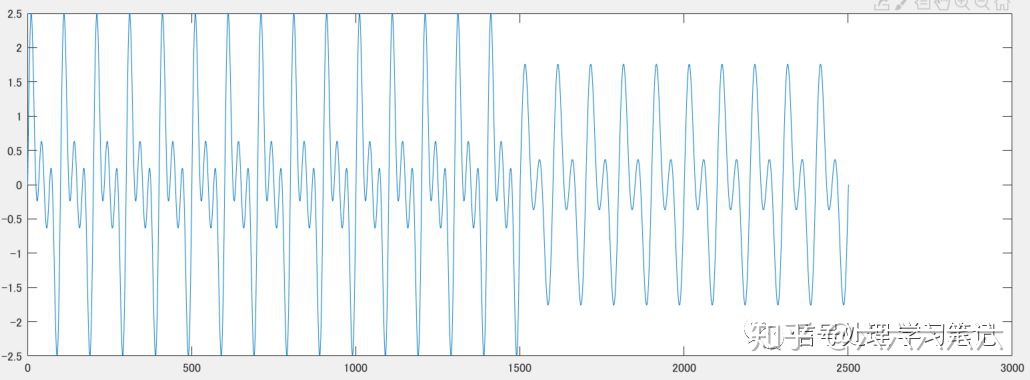
首先做一个验证用的原始曲线:
- 采样频率1000Hz10Hz,20
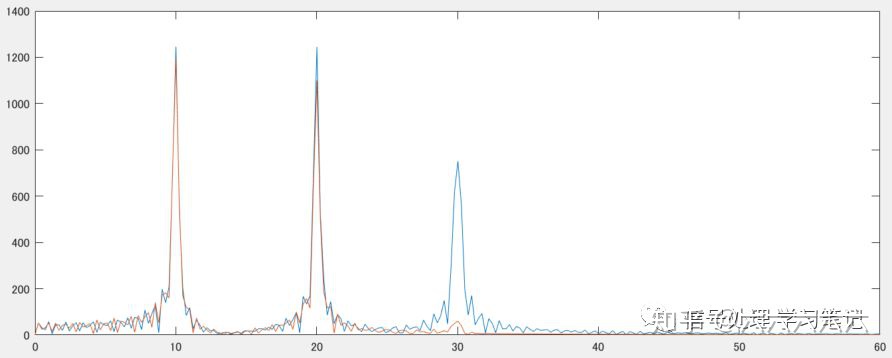
- 1-1500 point: 10Hz, 20Hz, 30Hz的混合波(30Hz为噪音)
- 1501-2500 point: 10Hz, 20Hz混合波(无噪音)
频谱图:
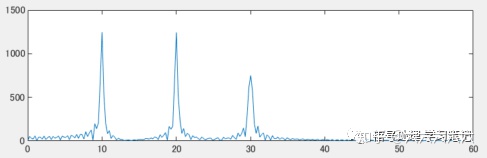
设计两个低通滤波器
- 20阶,25Hz低通滤波器
- 200阶,25Hz低通滤波器
幅频与相频特性:
FIR滤波器1:
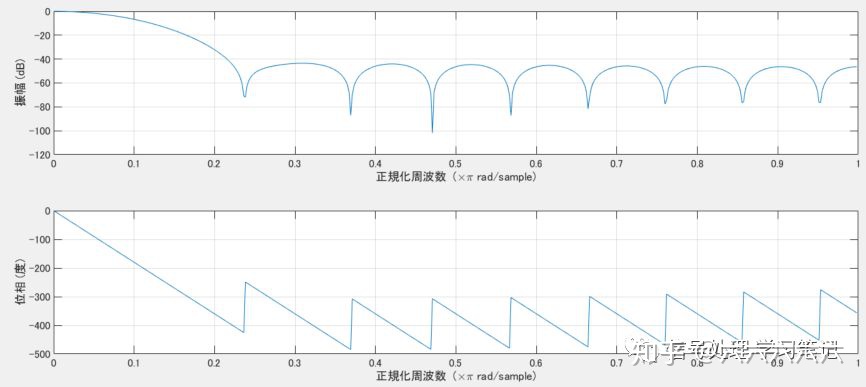
FIR滤波器2:
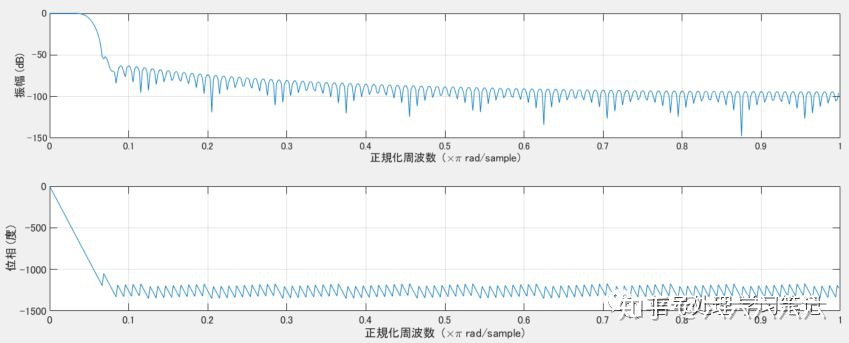
结果:
FIR滤波器1:
1. 群延迟为M/2=10 point,由于采样频率为1000Hz,延迟量为0.01s。
2. 由于阶数较低,迁移带较宽,所以30Hz的噪音依然存在。
3. 由于相位延迟为线性,所以未产生失真。
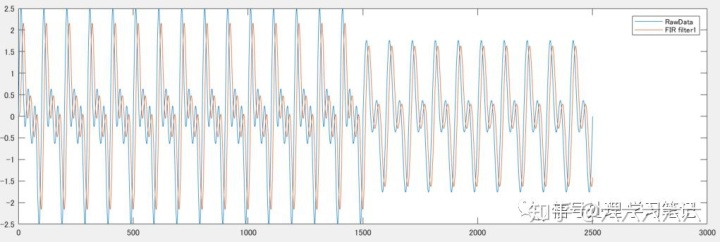
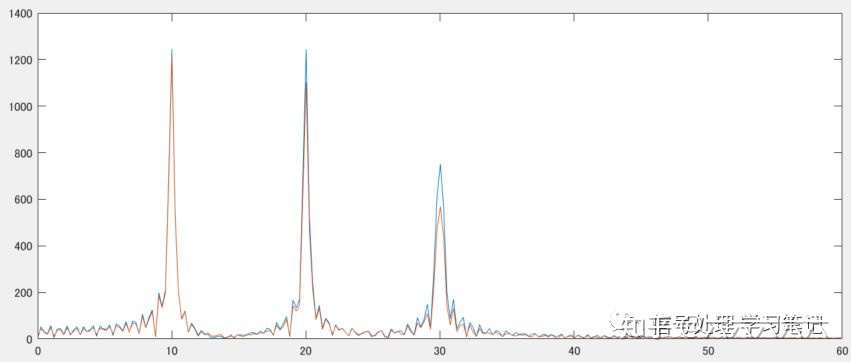
FIR滤波器2:
- 随着阶数的增加,延迟变大,M/2为100point,在采样频率为1000Hz时,正好是0.1s,为10Hz正弦波的一个周期。
- 随着阶数增加,迁移带变窄,所以30Hz噪音的滤波效果较好。
* 30Hz成分还有所残留是因为阶数还不够大,继续再增加阶数的话,噪音成分会完全消失。 - 由于相位延迟为线性,所以未产生失真。
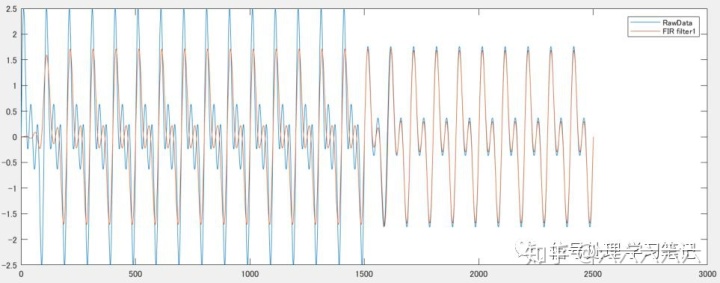
由于高阶FIR滤波器可以有效的近似到全域通过特性,并且完美的实现线性相位特性,因此在信号处理的预处理领域被广泛应用。
下一章讨论IIR滤波器,以及Zero phase IIR 滤波器的理论及验证。
我会把文章第一时间发在个人公众号里
有兴趣的朋友可以关注我大家一起学习讨论







)












