引言

规划求解工具是Excel软件中自带的一个功能非常强大的加载项/工具。它能够完成包括线性规划、整数线性规划等一般规模的数学优化问题的问题求解。更重要的是，无论是在Windows操作系统下，还是苹果电脑Mac平台下，这个工具都是免费的。下面就这个工具的安装和功能做一个简单介绍。

1 规划求解工具的安装

Excel软件安装时并不会自动安装规划求解工具，因此在使用规划求解工具前必须手工实现其安装。安装的步骤非常简单，下面以Office官网上给出的步骤，结合截图给出操作步骤：(1)打开Excel软件，在软件的左上角找到“文件”菜单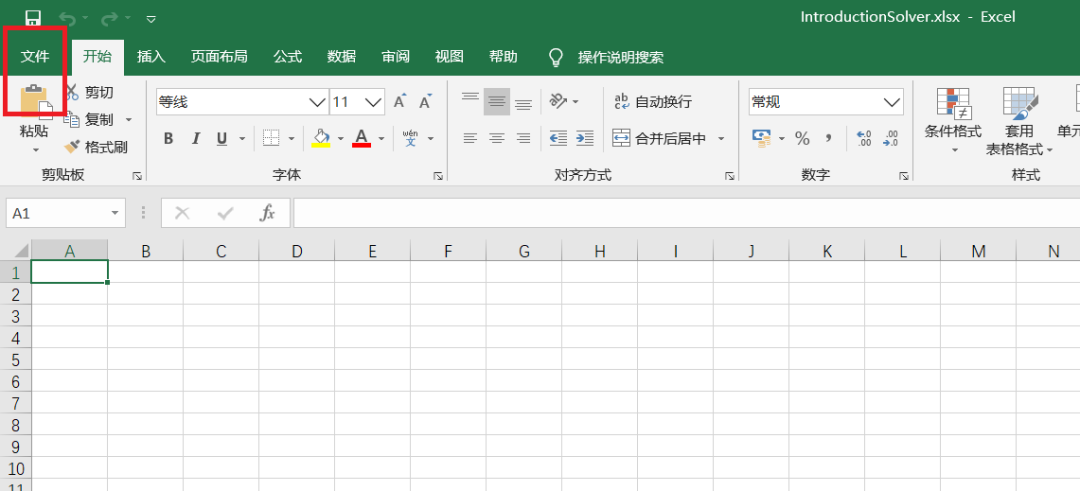(2)进入“文件”菜单，找到左下角的“选项”子菜单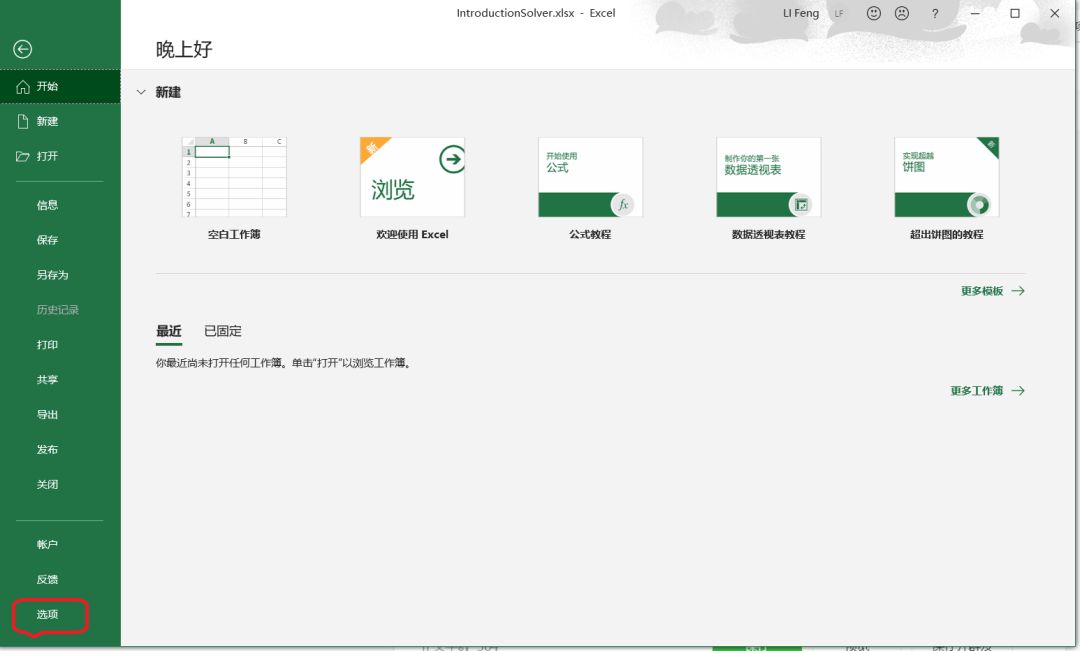(3)在“选项”窗口中，找到“加载项”栏目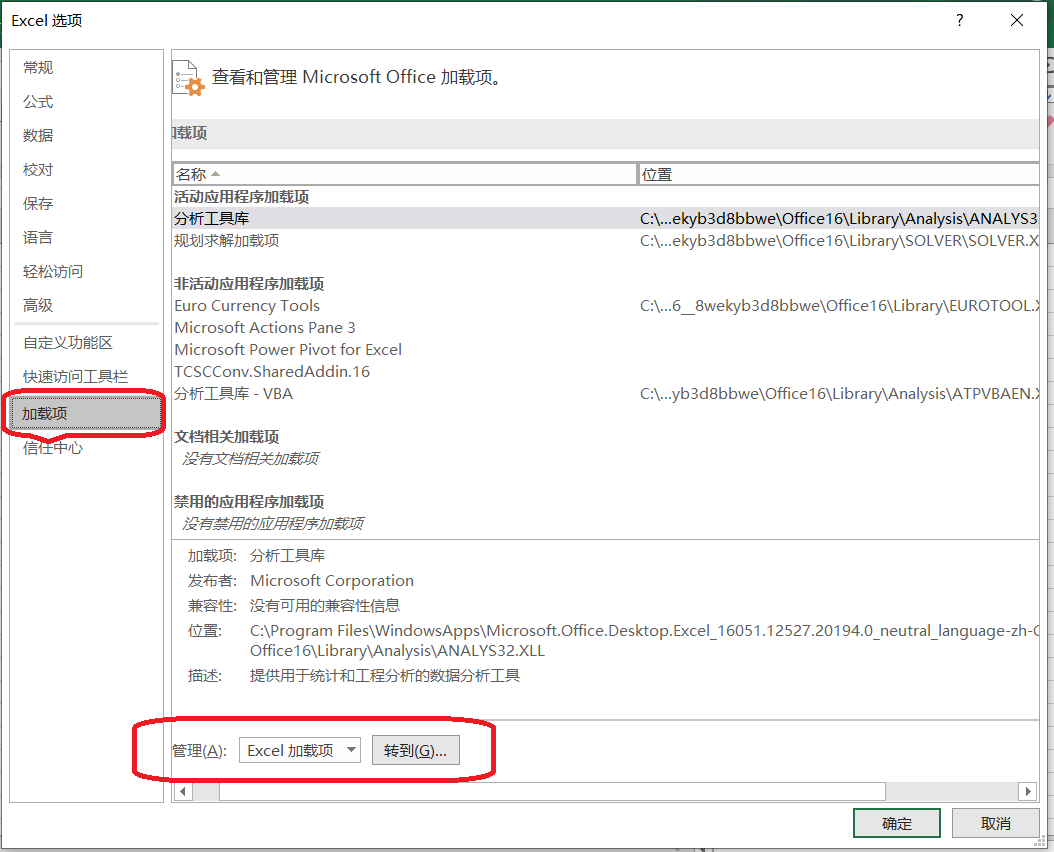

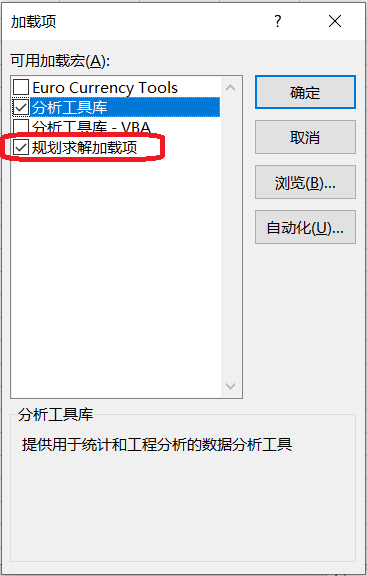在“管理”旁边，点击“转到”按钮。(4)在打开的“加载项”窗口，勾选“规划求解加载项”，确定后等待安装完成。【注】在这个“加载项”窗口中，还有一个非常实用和强大的工具包“分析工具库”。如果此时发现这个工具同样没有被勾选的话，建议同时勾选并安装。(5)安装成功后，在Excel软件的主菜单“数据”下面，就会出现“规划求解”的子菜单。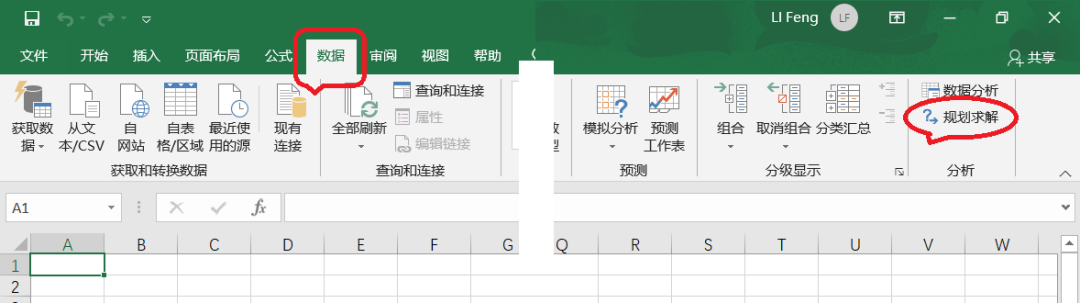(6)点击“规划求解”，就会打开“规划求解参数”窗口。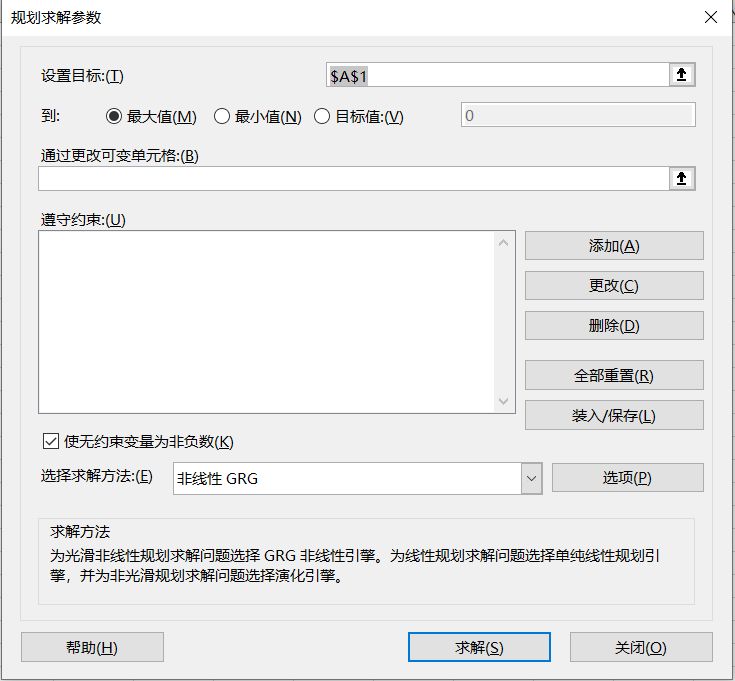出现如此的窗口，就表明“规划求解”工具安装成功。详细操作也可以参看下面视频。【注】这个工具的安装在微软Microsoft公司的Office官网给出了简单的说明，并给出了不同Excel版本下的安装说明。用户可以在微软公司的Office软件支持网站https://support.office.com上找到以类似“在Excel中加载规划求解加载项”或"Load the Solver add-in in Excel"标题的介绍性文章。

2 规划求解工具基本介绍

Excel软件的规划求解工具操作比较简单，窗口上内容主要可以分为三部分：(1)“设置目标”指出需要求解的优化问题的目标(单元格)。(2)“通过更改可变单元格”指出需要求解的优化问题的变量。(3)“遵守约束”指出需要求解的优化问题的约束条件。【注】窗口“选择求解方法”下拉列表框中，总共有三个选项，其适用范围也同时给出了解释。一般来说，线性规划问题可以采用“单纯线性规划”求解方法。

3 深入了解规划求解工具

规划求解工具由Frontline公司提供(https://solver.com)，在公司的网站中，对三个求解算法进行了说明(网站原文节选如下)：

The Microsoft Office Excel Solver tool uses several algorithms to find optimal solutions.

非线性GRG:

The GRG Nonlinear Solving Method for nonlinear optimization uses the Generalized Reduced Gradient (GRG2) code, which was developed by Leon Lasdon, University of Texas at Austin, and Alan Waren, Cleveland State University, and enhanced by Frontline Systems, Inc.

【翻译】此方法采用Generalized Reduced Gradient (GRG2)代码。开发者是...

单纯线性规划：

The Simplex LP Solving Method for linear programming uses the Simplex and dual Simplex method with bounds on the variables, and problems with integer constraints use the branch and bound method, as implemented by John Watson and Daniel Fylstra, Frontline Systems, Inc.

【翻译】线性规划问题采用单纯形法(Simplex)和对偶单纯形法(dual Simplex)，对于整数约束的线性规划问题采用分支定界方法(branch and bound)。开发者是...

演化：

The Evolutionary Solving Method for non-smooth optimization uses a variety of genetic algorithm and local search methods, implemented by several individuals at Frontline Systems, Inc.

【翻译】演化算法采用了遗传算法(genetic algorithm)和局部搜索方法(local search)。开发者是...

【注】规划求解工具的英文原名是Solver。计算结果情况呢？(网站原文节选如下)

With the Simplex LP Solving method, you can find a globally optimal solution given enough time – but you may have to settle for a solution that’s “close to optimal” found in a more reasonable amount of time.  With the GRG Nonlinear and Evolutionary Solving methods, you should expect a “good,” but not provably optimal solution.

【翻译】如果是单纯线性规划算法求解，你一定能够找出全局最优解(globally optimal solution)，但是你需要设置算法精度(close to optimal)。但是，非线性GRG和演化算法，你可能只能找到一个还不错(good)的解，但不一定是全局最优解。

这里所说的"设置"是指在“规划求解参数”窗口中，通过点击“选项”按钮，得到“选项”对话框。在这里，可以通过精确度设置来保证问题求解的“质量”。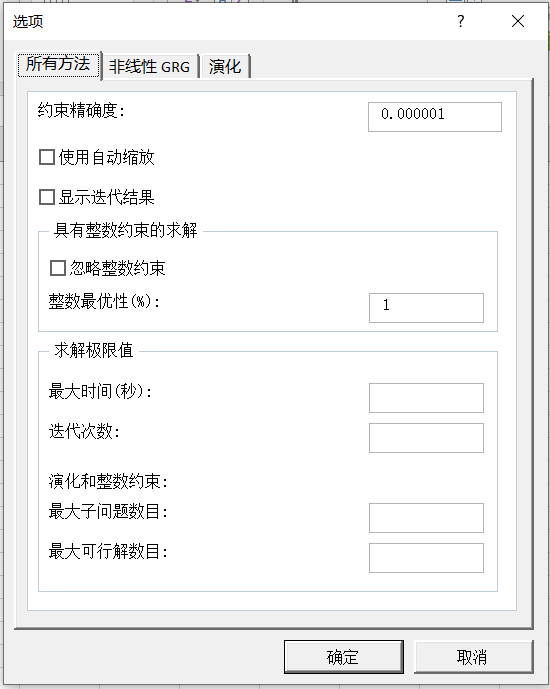最后，规划求解能做什么，不能做什么呢？网站原文节选如下：

*If your objective and constraints are linear functions of the decision variables, you can be confident of finding a globally optimal solution reasonably quickly, given the size of your model.  This is a linear programming problem; it is also a convex optimization problem (since all linear functions are convex).  The Simplex LP Solving method is designed for these problems.

【翻译】如果问题是线性规划问题，那么单纯形法最能够快速找到一个全局最优解，而求解速度取决于模型大小。

*If your objective and constraints are smooth nonlinear functions of the decision variables, solution times will be longer.  If the problem is convex, you can be confident of finding a globally optimal solution, but if it is non-convex, you can only expect a locally optimal solution – and even this may be hard to find.  The GRG Nonlinear Solving method is designed for these problems.

【翻译】如果问题是一个平滑的非线性问题，最好使用“非线性GRG”方法，计算时间会长一点。如果问题是一个凸函数(convex)，还是能够求出全局最优解；但是如果问题不是一个凸函数，那么这个问题求解非常困难。

*If your objective and constraints are non-smooth and non-convex functions of the decision variables (for example if you use IF, CHOOSE and LOOKUP functions whose arguments depend on decision variables), the best you can hope for is a “good” solution (better than the initial values of the variables), not a locally or globally optimal solution.  The Evolutionary Solving method is designed for these problems.

【翻译】如果问题不是一个平滑和凸函数，例如，你在模型中用了类似Excel函数IF等，那么问题求解比较困难。此时，你需要使用“演化”方法。

*You can use integer, binary, and alldifferent constraints on variables with all three Solving methods.  However, these constraints make the problem non-convex and much harder to solve.

【翻译】如果问题中增加了整数、0-1变量或者alldifferent约束形式，这个问题就变成了非凸函数，求解起来也非常困难。

4 总结

对于一般问题，采用规划求解工具进行求解，不会有太大问题。但是，如果问题中出现了非线性、整数约束等，最好还是选用更加高级的商业工具，如matlab, ampl, cplex, ...。

｜编辑：胡锦亚