如何用三元组表表示下列稀疏矩阵_盘一盘 Python 系列特别篇21之：SciPy 稀疏矩阵...

引言

和稠密矩阵相比，稀疏矩阵的最大好处就是节省大量的内存空间来储存零。稀疏矩阵本质上还是矩阵，只不过多数位置是空的，那么存储所有的 0 非常浪费。稀疏矩阵的存储机制有很多种 (列出常用的五种)：

COO (Coordinate List Format)：座标格式，容易创建但是不便于矩阵计算，用 coo_matrix
CSR (Compressed Sparse Row)： 压缩行格式，不容易创建但便于矩阵计算，用 csr_matri
CSC (Compressed Sparse Column)： 压缩列格式，不容易创建但便于矩阵计算，用 csc_matrix
LIL (List of List): 内嵌列表格式，支持切片但也不便于矩阵计算，用 lil_matrix
DIA (Diagnoal)：对角线格式，适合矩阵计算，用 dia_matrix

在 SciPy 中稀疏矩阵一共有七种，剩余的两种类型 BSR 和 DOK 本贴不做研究。有兴趣的读者可以去官网去查询。

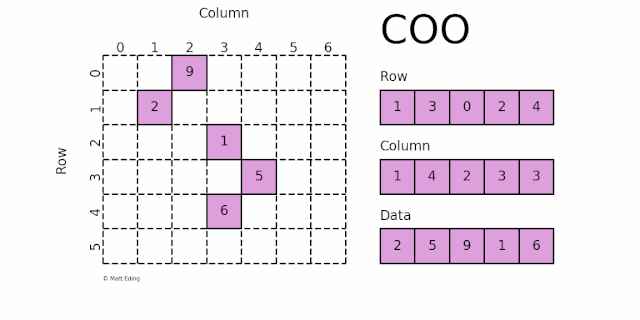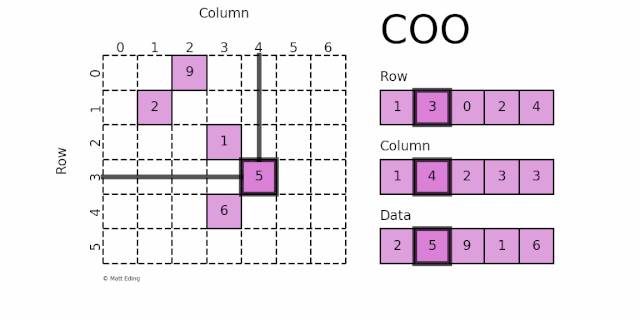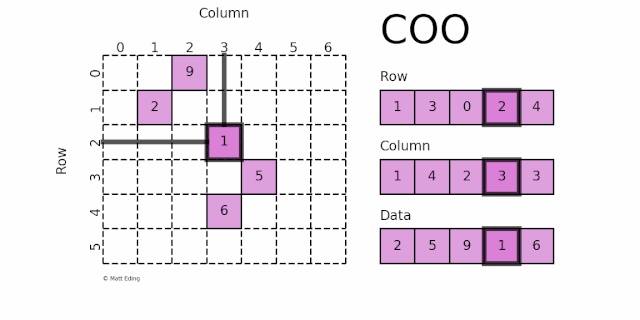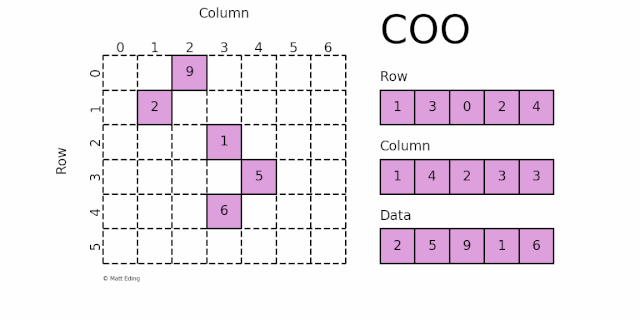
COO

采用三元组 (row, col, data) 的形式来存储矩阵中非零元素的信息，即把非零值 data 按着行坐标 row 和纵坐标 col 写成两个列表。如下图所示：

坐标 (1, 1) 对应的数据 2
坐标 (3, 4) 对应的数据 5
坐标 (0, 2) 对应的数据 9
坐标 (2, 3) 对应的数据 1
坐标 (4, 3) 对应的数据 6

在实际使用中，用 coo_matrix() 语法来创建矩阵，注意产出矩阵的格式是COOrdinate。

values = [1, 2, 3, 4]rows = [0, 1, 2, 3]cols = [1, 3, 2, 0]A = sp.coo_matrix((values, (rows, cols)), shape=[4, 4])A

<4x4 sparse matrix of type 'numpy.int32'>'with 4 stored elements in COOrdinate format>

检查矩阵 A 的形状、数据类型、维度和非零值的个数。

A.shape, A.dtype, A.ndim, A.nnz

((4, 4), dtype('int32'), 2, 4)

检查矩阵 A 的行坐标、列坐标和数据。

A.row, A.col, A.data

(array([0, 1, 2, 3], dtype=int32),
 array([1, 3, 2, 0], dtype=int32),
 array([1, 2, 3, 4]))

如果想看 A 中的元素，我们可用 toarray() 转换成 numpy 数组显示出来。

A.toarray()

array([[0, 1, 0, 0],
       [0, 0, 0, 2],
       [0, 0, 3, 0],
       [4, 0, 0, 0]])

COO 矩阵的元素无法进行增删改操作，一般创建成功之后可以转化成其他格式的稀疏矩阵 (如 CSR, CSC) 进行转置、矩阵乘法等操作，或者转成转成 LIL 做切片。

A.tocsr()

<4x4 sparse matrix of type 'numpy.intc'>'with 4 stored elements in Compressed Sparse Row format>

A.tolil()

<4x4 sparse matrix of type 'numpy.intc'>'with 4 stored elements in List of Lists format>

可视化矩阵 A

plt.spy(A);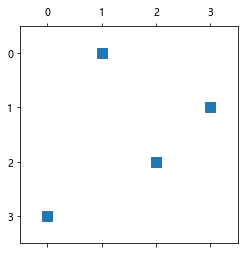

CSR

由三个一维数组 indptr, indices, data 组成。这种格式要求矩阵元按行顺序存储，每一行中的元素可以乱序存储。那么对于每一行就只需要用一个指针表示该行元素的起始位置即可。

indices 存储每行中数据的列号，与属性 data 中的元素一一对应
indptr 存储每行数据元素的起始位置

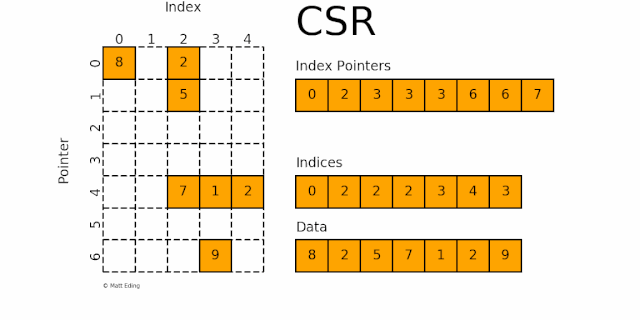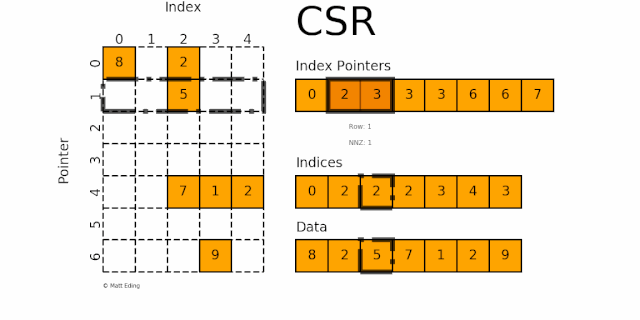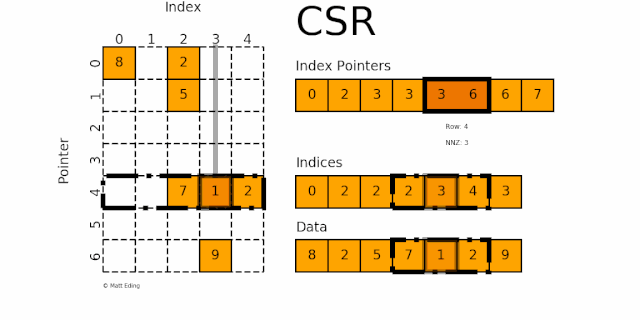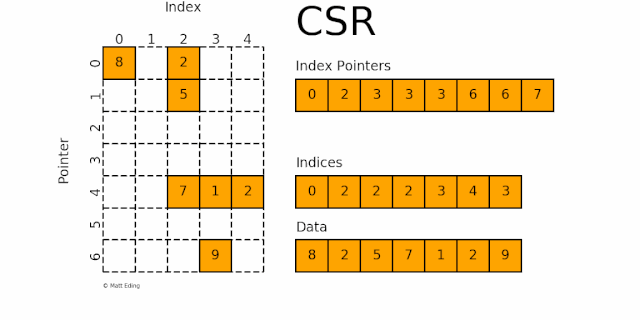
如下图所示：

第 1 行：indptr 0-2 指 indices[0:2] 的值即 0 和 2，分别又指第 0 和 2 列，对应的数据 8 和 2
第 2 行：indptr 2-3 指 indices[2:3] 的值即 2，分别又指第 2 列，对应的数据 5
第 3 行：indptr 3-3 指 indices[3:3] 的值为空，无数据
第 4 行：indptr 3-3 指 indices[3:3] 的值为空，无数据
第 5 行：indptr 3-6 指 indices[3:6] 的值即 2，3 和 4，分别又指第 2，3 和 4 列，对应的数据 7，1 和 2
第 6 行：indptr 6-6 指 indices[6:6] 的值为空，无数据
第 7 行：indptr 6-7 指 indices[6:7] 的值即 3，分别又指第 3 列，对应的数据 9

规律：indptr 的长度等于矩阵行数加 1，而第 i 行的列数，就是 indices[indptr[i]:indptr[i+1]]。

用 csr_matrix() 语法用来创建矩阵，注意产出矩阵的格式是 Compressed Sparse Row。

data = np.array([1, 2, 3, 4, 5, 6])indices = np.array([0, 2, 2, 0, 1, 2])indptr = np.array([0, 2, 3, 6])A = sp.csr_matrix((data, indices, indptr), shape=(3, 3))A

<3x3 sparse matrix of type 'numpy.int32'>'with 6 stored elements in Compressed Sparse Row format>

检查矩阵 A 的形状、数据类型、维度和非零值的个数。

A.shape, A.dtype, A.ndim, A.nnz

((3, 3), dtype('int32'), 2, 6)

检查矩阵 A 的列索引、索引指针和数据。

A.indices, A.indptr, A.data

(array([0, 2, 2, 0, 1, 2]), array([0, 2, 3, 6]), array([1, 2, 3, 4, 5, 6]))

如果想看 A 中的元素，我们可用 toarray() 转换成 numpy 数组显示出来。

A.toarray()

array([[1, 0, 2],
       [0, 0, 3],
       [4, 5, 6]])

可视化矩阵 A

plt.spy(A);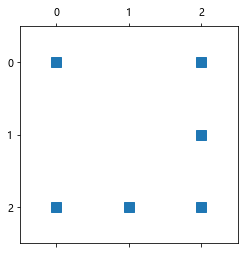

CSC

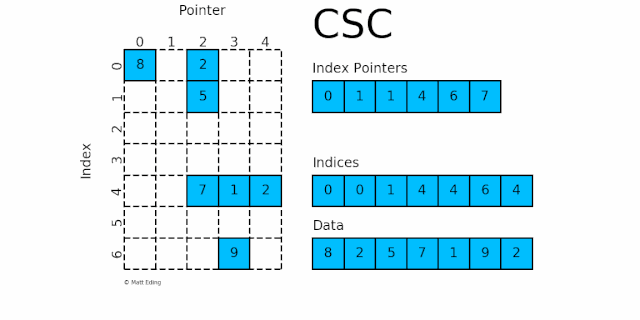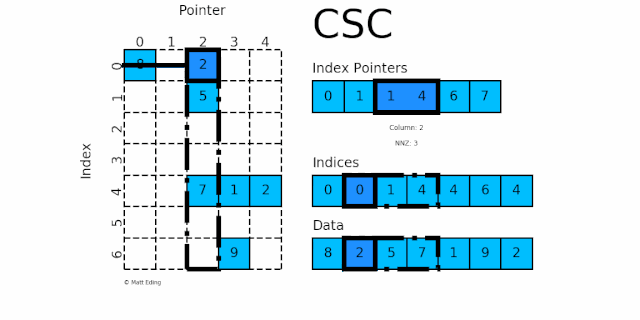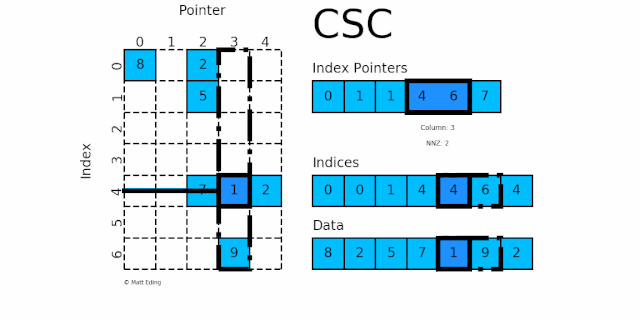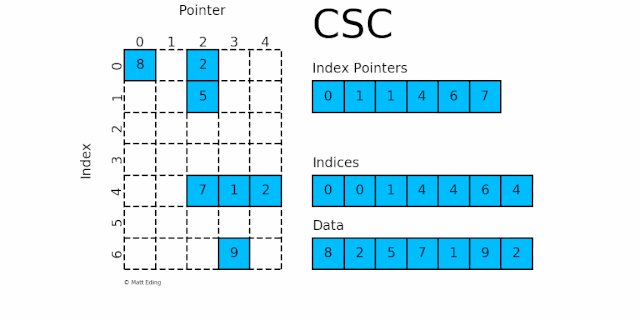
csc_matrix 和 csr_matrix 正好相反，即按列压缩的稀疏矩阵存储方式，同样由三个一维数组 indptr, indices, data 组成，

indices 存储每列中数据的行号，与属性 data 中的元素一一对应
indptr 存储每列数据元素的起始位置

如下图所示：

第 0 列：indptr 0-1 指 indices[0:1] 的值即 0，分别又指第 0 行，对应的数据 8
第 1 列：indptr 1-1 指 indices[1:1] 的值为空，无数据
第 2 列：indptr 1-4 指 indices[1:4] 的值即 0，1 和 4，分别又指第 0，1 和 4 行，对应的数据 2，5 和 7
第 3 列：indptr 4-6 指 indices[4:6] 的值即 4 和 6，分别又指第 4 和 6 行，对应的数据 1 和 9
第 4 列：indptr 6-7 指 indices[6:7] 的值即 4，分别又指第 4 行，对应的数据 2

规律：indptr 的长度等于矩阵列数加 1，而第 i 列的行数，就是 indices[indptr[i]:indptr[i+1]]。

用 csc_matrix() 语法用来创建矩阵，注意产出矩阵的格式是 Compressed Sparse Column。

data = np.array([1, 2, 3, 4, 5, 6])indices = np.array([0, 2, 2, 0, 1, 2])indptr = np.array([0, 2, 3, 6])A = sp.csc_matrix((data, indices, indptr), shape=(3, 3))A

<3x3 sparse matrix of type 'numpy.int32'>'with 6 stored elements in Compressed Sparse Column format>

检查矩阵 A 的形状、数据类型、维度和非零值的个数。

A.shape, A.dtype, A.ndim, A.nnz

((3, 3), dtype('int32'), 2, 6)

检查矩阵 A 的行索引、索引指针和数据。

A.indices, A.indptr, A.data

(array([0, 2, 2, 0, 1, 2]), array([0, 2, 3, 6]), array([1, 2, 3, 4, 5, 6]))

如果想看 A 中的元素，我们可用 toarray() 转换成 numpy 数组显示出来。

A.toarray()

array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]])

可视化矩阵 A

plt.spy(A);

LIL

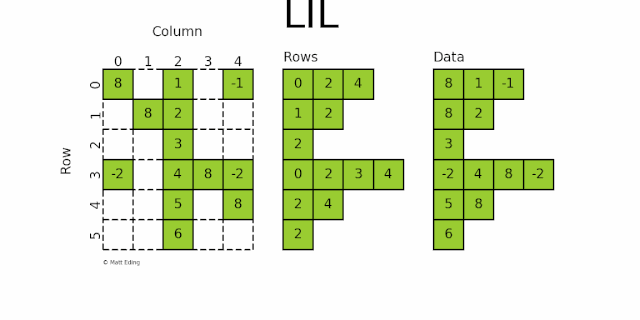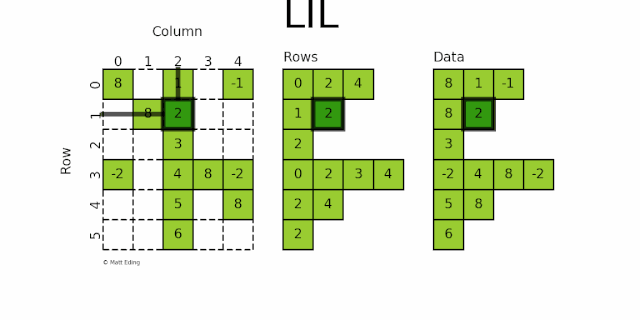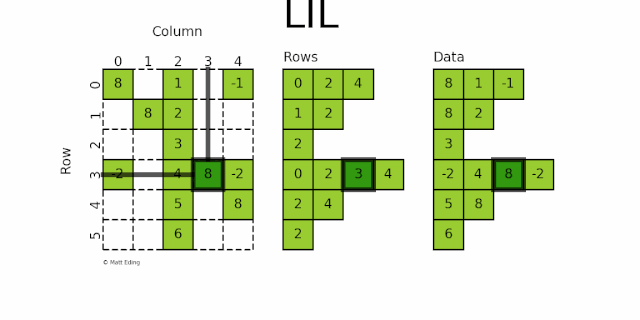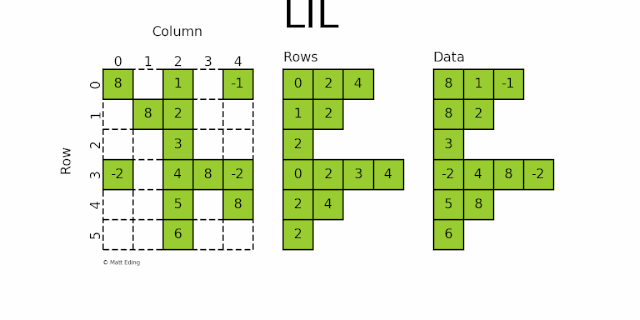
lil_matrix 使用两个嵌套列表存储稀疏矩阵：

data 保存每行中的非零元素的值
rows 保存每行非零元素所在的列号 (列号是按顺序排的)。

这种格式很适合逐个添加元素，并且能快速获取行相关的数据。如下图所示：

第 0 行：列号为 0，2，4，对应的数据为 8，1，-1
第 1 行：列号为 1，2，对应的数据为 8，2
第 2 行：列号为 2，对应的数据为 3
第 3 行：列号为 0，2，3，4，对应的数据为 -2，4，8，-2
第 4 行：列号为 2，4，对应的数据为 5，8
第 5 行：列号为 2，对应的数据为 6

用 lil_matrix() 语法用来创建矩阵，注意产出矩阵的格式是 Lists of Lists。

data = [[8,0,1,0,-1],        [0,8,2,0,0],        [0,0,3,0,0],        [-2,0,4,8,-2],        [0,0,5,0,8],        [0,0,6,0,0]]A = sp.lil_matrix(data)A

<6x5 sparse matrix of type 'numpy.intc'>'with 13 stored elements in List of Lists format>

检查矩阵 A 的每行的非零值对应的列索引。

A.rows

array([list([0, 2, 4]), list([1, 2]), list([2]), list([0, 2, 3, 4]),
       list([2, 4]), list([2])], dtype=object)

如果想看 A 中的元素，我们可用 toarray() 转换成 numpy 数组显示出来。

A.toarray()

array([[ 8, 0, 1, 0, -1],
       [ 0, 8, 2, 0, 0],
       [ 0, 0, 3, 0, 0],
       [-2, 0, 4, 8, -2],
       [ 0, 0, 5, 0, 8],
       [ 0, 0, 6, 0, 0]], dtype=int32)

可视化矩阵 A

plt.spy(A);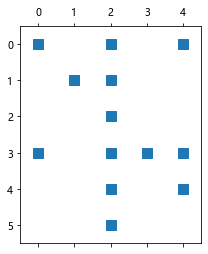

DIA

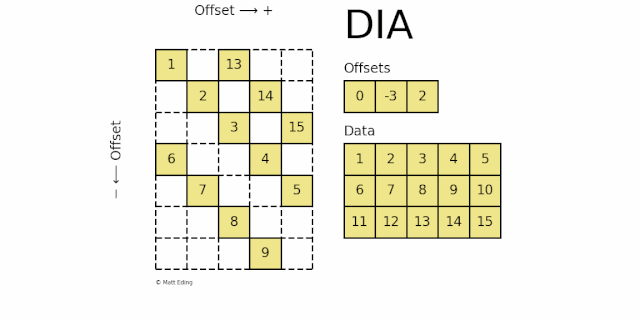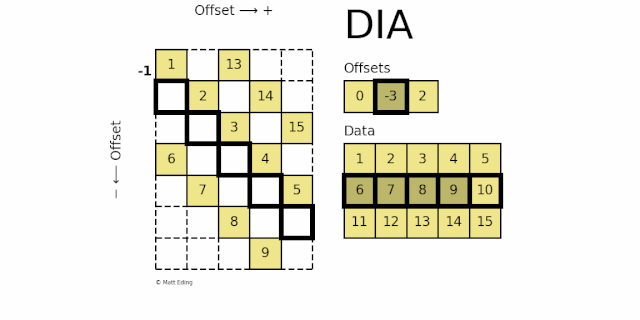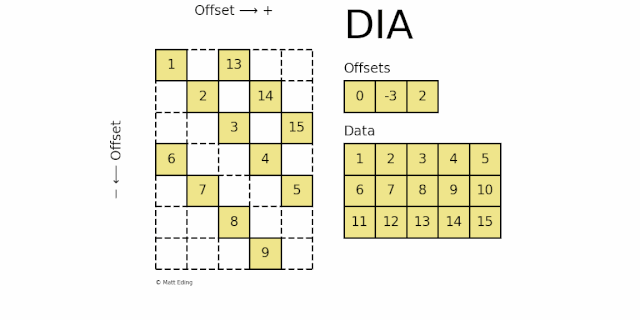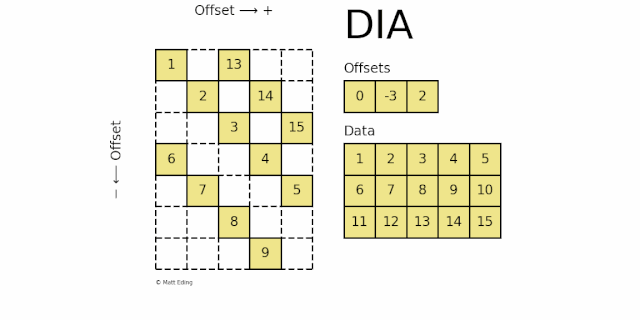
dia_matrix 按对角线的存储方式。稀疏矩阵使用 offsets 和 data 两个矩阵来表示，其中offsets 表示 data 中每一行数据在原始稀疏矩阵中的对角线位置 k：

k > 0, 对角线往右上方移动 k 个单位
k < 0, 对角线往左下方移动 k 个单位
k = 0，主对角线

如下图所示：

offset 0 对应的数据 [1,2,3,4,5] 在主对角线上
offset -3 对应的数据 [6,7,8,9,10] 在主对角线左下方移动 3 个单位
offset 2 对应的数据 [11,12,13,14,15] 在对角线上右上方移动 2 个单位

用 dia_matrix() 语法用来创建矩阵，注意产出矩阵的格式是 DIAgonal。

data = np.arange(1,13).reshape(3,-1)offset = [-1, 0, 1]A = sp.dia_matrix( (data, offset), shape=(4,4) )A

<4x4 sparse matrix of type 'numpy.int32'>'with 10 stored elements (3 diagonals) in DIAgonal format>

检查矩阵 A 的平移单位。

A.offsets

array([-1, 0, 1], dtype=int32)

如果想看 A 中的元素，我们可用 toarray() 转换成 numpy 数组显示出来。

A.toarray()

array([[ 5, 10, 0, 0],
       [ 1, 6, 11, 0],
       [ 0, 2, 7, 12],
       [ 0, 0, 3, 8]])

可视化矩阵 A

plt.spy(A);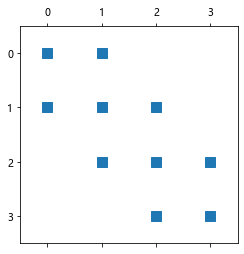

此外，在 sp.sparse 模块里还有一些直接创建稀疏矩阵的函数：

eye 生成稀疏单位对角阵
diags 构建稀疏对角阵
spdiags 构建稀疏对角阵

假设我们想生成一个方阵，主对角线上面是 -2，上下次对角线上的值为 1。

方法一：用 eye

N = 5A = sp.eye(N, k=1) - 2 * sp.eye(N) + sp.eye(N, k=-1)A.toarray()

array([[-2., 1., 0., 0., 0.],
       [ 1., -2., 1., 0., 0.],
       [ 0., 1., -2., 1., 0.],
       [ 0., 0., 1., -2., 1.],
       [ 0., 0., 0., 1., -2.]])

方法二：用 diags

A = sp.diags([1, -2, 1], [1, 0, -1], (N, N), format='csc')A.toarray()

array([[-2., 1., 0., 0., 0.],
       [ 1., -2., 1., 0., 0.],
       [ 0., 1., -2., 1., 0.],
       [ 0., 0., 1., -2., 1.],
       [ 0., 0., 0., 1., -2.]])

方法三：用 spdiags

data = np.vstack( [np.repeat(1,N), np.repeat(-2,N), np.repeat(1,N)] )A = sp.spdiags( data, [1, 0, -1], N, N )A.toarray()

array([[-2., 1., 0., 0., 0.],
       [ 1., -2., 1., 0., 0.],
       [ 0., 1., -2., 1., 0.],
       [ 0., 0., 1., -2., 1.],
       [ 0., 0., 0., 1., -2.]])

三种方法都得到一样的结果，但是用 diags 方法代码最简洁些。但是如果对角线上的值都不一样，那么只能用 spdiags 方法，原因是它的参数是数组，而不是元素。

在金工中一维 PDE 有限差分离散之后都是这种类型的三对角矩阵 (tri-diagnol)，因此要熟练掌握用 diags/spdiags 方法来创建金工需要的“稀疏矩阵”。

总结

从官网资料看出，一般使用 lil_matrix 来构建矩阵效率最高。由于 LIL 形式是基于行的，因此它能够很高效的转为 CSR，但是转为 CSC 的效率相对较低。

如果要执行矩阵乘法或转置，将它们转换成 CSC 或 CSR 格式，效率最高。

总之，在运算稀疏矩阵时，绝对绝对不要直接使用 NumPy！

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

如果觉得好，关注、转发、在看三连发走起 666~~~

福利来一波~~~

关注公众号回复以下信息送免费资料
回复Jenkins 领取Jenkins学习资料回复Jmeter 领取Jmeter学习资料

回复Java 领取Java学习资料

回复Python 领取python入门资料