1 两因素方差分析的形式
多因素方差分析针对的是多因素完全随机设计。包含两个及以上的自变量,为便于讲解,本文以两因素方差分析为例。
在一个两因素完全随机设计中,自变量
等组设计的具体形式如下:
若各组观测值
其中
两因素方差分析的逻辑是对变异进行比较。通过对平方和(Sum of Squares)和自由度(Degree of Freedom)的分解,利用公式:
计算出各主效应方差,交互作用方差和组内方差(即误差方差)。各主效应和交互作用的方差与误差方差的差异(比值)体现了该效应的显著性。而且在零假设为真的情况下,该比值服从F分布,进而分别完成各效应的假设检验。
具体的分解如下图:
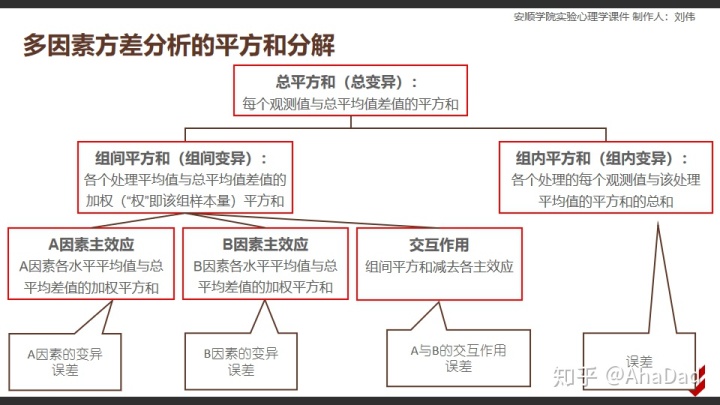
常规的流程大家都非常熟悉,不再赘述。接下来换个角度,从多元线性回归来看一看两因素方差分析。
2 两因素方差分析的线性模型
模型的基本形式
两因素方差分析的线性模型可以表示为:
其中
通常,我们让:
其中
2.2.4和2.2.5式需要稍微推导一下,有兴趣的同学可以自己动手试试,没兴趣忽略就好
据此,可将2.1式写为:
其中:
是观测值
是总平均,相当于是截距
是随机误差,且独立同分布
模型表达的意思是:每一个观测值
例如,如果某被试接受的是自变量
引入虚拟变量
为了便于理解,我们可以引入虚拟变量
意味着:在
例如:对第
可以发现,当把虚拟变量带入2.3式之后得到:
2.4式可看成是一个包含
此时
此时
是不是眼花缭乱?哈哈。
如果从矩阵的角度来看,此时的
别担心,我们还有2.2.2-2.2.5这几个式子,利用这几个式子将上述取值改为:(又要眼花缭乱了)
此时利用2.2.1和2.2.2式将
同理,可将交互作用的虚拟变量改为:
注意到对角线的子矩阵,以及最后一行的各矩阵。特别是最后一行
3 对单因素方差分析的线性模型进行多元回归
提示:该部分直接用公式推导实在太麻烦了,所以用一个数据例子来进行说明。
以一个3×2的两因素完全随机设计为例,其中A因素个水平,B因素两个水平,每个处理之下一共4个观测值。
将观测值
接下来,利用python的statemodels进行计算:
from statsmodels.formula.api import ols #拟合线性模型的包
from statsmodels.stats.anova import anova_lm#进行方差分析的包
import pandas as pd
import numpy as np
data={'XA1': [1,1,1,1, 1, 1, 1, 1,0,0,0,0,0,0,0,0,-1,-1,-1,-1,-1,-1,-1,-1],'XA2': [0,0,0,0, 0, 0, 0, 0,1,1,1,1,1,1,1,1,-1,-1,-1,-1,-1,-1,-1,-1],'XB1': [1,1,1,1,-1,-1,-1,-1,1,1,1,1,-1,-1,-1,-1,1,1,1,1,-1,-1,-1,-1],'XAB11':[1,1,1,1,-1,-1,-1,-1,0,0,0,0,0,0,0,0,-1,-1,-1,-1,1,1,1,1],'XAB21':[0,0,0,0,0,0,0,0,1,1,1,1,-1,-1,-1,-1,-1,-1,-1,-1,1,1,1,1],'Y':[5,3,4,2,6,3,5,5,7,6,7,8,8,7,8,5,9,7,5,7,10,12,11,7],'A':[1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,3,3,3,3,3,3,3,3],'B':[1,1,1,1,2,2,2,2,1,1,1,1,2,2,2,2,1,1,1,1,2,2,2,2]
}#其中前5行是虚拟变量,Y是观测值,A,B是分类变量
df=pd.DataFrame(data)
model_lin=ols('Y~XA1+XA2+XB1+XAB11+XAB21',data=df).fit()#用虚拟变量进行回归
model_anova=ols('Y~C(A)*C(B)',data=df).fit()#用分类变量进行方差分析
anova_Result=anova_lm(model_anova)print(anova_Result)df sum_sq mean_sq F PR(>F)
C(A) 2.0 79.083333 39.541667 17.905660 0.000052
C(B) 1.0 12.041667 12.041667 5.452830 0.031315
C(A):C(B) 2.0 9.083333 4.541667 2.056604 0.156887
Residual 18.0 39.750000 2.208333 NaN NaN
#利用方差分析结果计算决定系数,组间平方和(主效应与交互作用之和)/总平方和
R_square=np.sum(anova_Result.sum_sq[0:3])/np.sum(anova_Result.sum_sq)
print(R_square)0.7159869008633524
#打印回归分析结果
print(model_lin.summary())OLS Regression Results
==============================================================================
Dep. Variable: Y R-squared: 0.716
Model: OLS Adj. R-squared: 0.637
Method: Least Squares F-statistic: 9.075
Date: Sat, 11 Apr 2020 Prob (F-statistic): 0.000191
Time: 18:02:59 Log-Likelihood: -40.109
No. Observations: 24 AIC: 92.22
Df Residuals: 18 BIC: 99.29
Df Model: 5
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 6.5417 0.303 21.566 0.000 5.904 7.179
XA1 -2.4167 0.429 -5.633 0.000 -3.318 -1.515
XA2 0.4583 0.429 1.068 0.299 -0.443 1.360
XB1 -0.7083 0.303 -2.335 0.031 -1.346 -0.071
XAB11 0.0833 0.429 0.194 0.848 -0.818 0.985
XAB21 0.7083 0.429 1.651 0.116 -0.193 1.610
==============================================================================
Omnibus: 1.556 Durbin-Watson: 2.330
Prob(Omnibus): 0.459 Jarque-Bera (JB): 1.295
Skew: -0.535 Prob(JB): 0.523
Kurtosis: 2.614 Cond. No. 1.73
==============================================================================Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
#利用回归模型输出各预测值
model_lin.predict()array([ 3.5 , 3.5 , 3.5 , 3.5 , 4.75, 4.75, 4.75, 4.75, 7. ,7. , 7. , 7. , 7. , 7. , 7. , 7. , 7. , 7. ,7. , 7. , 10. , 10. , 10. , 10. ])
#利用回归模型输出参数估计值
model_lin.paramsIntercept 6.541667
XA1 -2.416667
XA2 0.458333
XB1 -0.708333
XAB11 0.083333
XAB21 0.708333
dtype: float64
#输出原始观测值的总均值
np.mean(df['Y'])6.541666666666667可见,用常规的方差分析计算出来的结果与回归分析一致,决定系数
绕了这么半天,似乎说了好多废话。有同学可能会嫌弃,认为我把简单的事情搞复杂了。确实这样理解很复杂,但是只有这样理解了,我们才能搞清楚什么是Ⅰ型平方和以及Ⅲ型平方和。这两种平方和专门针对多因素方差分析,在等组设计中二者没有区别,但是非等组设计中二者区别就大了,反正我最终是通过回归才搞清楚。
关于Ⅰ型平方和以及Ⅲ型平方和,我会专门写一篇文章来介绍。
4 结论
- 多元回归的结果与方差分析的结果是一致的
- 将多因素方差分析转换为回归分析时,要注意虚拟变量的取值,特别是交互作用的虚拟变量。
- 通过回归来理解方差分析,有助于我们理解Ⅰ型平方和以及Ⅲ型平方和(另开文章介绍)

)


)

)


)

)


)


)
)
