一,查找存在的一个数,该数在列表中唯一
二分法查找是针对有序数据的查找方法,时间复杂度是O(logn)。。
其中 n/2^k=1 时,k 的值就是总共缩小的次数。而每一次缩小操作只涉及两个数据的大小比较,所以,
经过了 k 次区间缩小操作,时间复杂度就是 O(k)。通过 n/2^k=1,我们可以求得 k=log2n,所以时间复杂度就是O(K),也就是O(logn)。
方法一,循环
实际上,mid=(low+high)/2 这种写法是有问题的,因为low和high很大的时候,两者之和可能会溢出,应该写为low+(high-low)/2,
更好的话写成,low+((high-low)>>1)
#有序列表的二分法,最简单版
def binary_search(array,value):if len(array) <= 1:return arraylow=0high=len(array)-1while(low<=high):#多这种写法mid = low+((high-low)>>1)if value==array[mid]:return mid,array[mid]elif value>array[mid]:low=mid+1else:high=mid-1return -1,-1
a=[0,1,1.5,2,3,4,9]
index,res=binary_search(a,9)
print('index={},res={}'.format(index,res))方法二,递归
#有序列表的二分法,最简单版
def binary_search(array,low,high,value):if low>high:return -1mid = low + int((high - low) >> 1)if value==array[mid]:return mid,array[mid]elif value>array[mid]:low=mid+1return binary_search(array,low,high,value)else:high=mid-1return binary_search(array, low, high, value)
def binary_search_merge(array,value):return binary_search(array,0,len(array)-1,value)
a=[0,1,2,3,4,9]
index,res=binary_search_merge(a,9)
print('index={},res={}'.format(index,res))缺点:(1)依赖的是顺序表结构,比如数组,不能用于链表,(2)需要先排好序,而排序的最低时间复杂度是O(nlogn),(3)不适用于小数据量(4)二分查找更适合处理静态数据,也就是没有频繁的数据插入、删除操作。
二,查找第一个值等于给定值的元素(存在多个值)
target大于目标值,左边界就变大,当找到等于的就返回左边界值,也就是第一个值了
def searchLeft(nums, target):left, right = 0, len(nums) - 1while left <= right:middle = left + (right - left) // 2if nums[middle] < target:left = middle + 1else:right = middle - 1return leftnums = [5, 7, 7, 8, 8, 10]
target = 8
# nums = [0, 1, 8, 8, 9, 9, 9]
# target = 9
res = searchLeft(nums, target)
print(res)
三,查找最后一个值等于给定值的元素(存在多个值)
target大于等于左边界的值,这时左边界值越来越大直到找到最后一个才返回
def searchRight(nums, target):left, right = 0, len(nums) - 1while left <= right:middle = left + (right - left) // 2if nums[middle] <= target: # 加个等于符号 这样left就可以找到最后一个left = middle + 1else:right = middle - 1return left - 1
nums = [5, 7, 7, 8, 8, 10]
target = 8
# nums = [0, 1, 8, 8, 9, 9, 9]
# target = 9
res = searchRight(nums, target)
print(res)四,查找第一个大于等于给定值的元素(存在多个值)
#查找第一个大于等于目标值的数
def binary_search(array, value):left = 0right = len(array) - 1while left < right:middle = left + (right - left)//2print('====middle:', middle)if array[middle] < value:left = middle + 1else:right = middle# print(middle)return right, array[right]
# a = [0,1,7,7,7,9,9]
a = [0, 1, 1, 1, 1]
index, res = binary_search(a, 1)
print('index={},res={}'.format(index, res))
五. 查找第一个大于给定值的元素(存在多个值)
#查找第一个大于目标值的数
def binary_search(array, value):left = 0right = len(array) - 1while left < right:middle = left + (right - left)//2if array[middle] <= value:left = middle + 1else:right = middle# print(middle)return right, array[right]
a = [0,1,7,7,7,9,9]
# a = [0, 1, 1, 1, 1]
index, res = binary_search(a, 7)
print('index={},res={}'.format(index, res))六,查找最后一个小于给定值的元素(存在多个值)
def binary_search(array,value):if len(array) <= 1:return arraylow=0high=len(array)-1while(low<=high):#多这种写法mid = low+((high-low)>>1)#中间值小于valueif array[mid]<value:#中间值的前一位大于等于value或者mid==len(array)-1if array[mid+1]>value or mid==len(array)-1:return mid,array[mid]else:low=mid+1else:high=mid-1return -1,-1
a=[0,1,7,7,7,9,9]
index,res=binary_search(a,8)
print('index={},res={}'.format(index,res))
实际上,二分法更适用于‘近似’查找问题,这类问题二分法查找优势更加明显,用其他数据结构比如散列表,二叉树就比较难实现了。
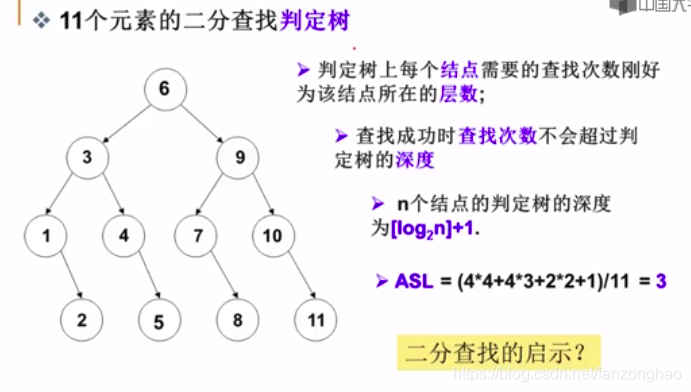
由此引出树:
对于1到11的元素,首先以6为分节点,然后不断分。。。







...)




算出长字符串中包含多少个短字符串)








