贪心算法+回溯算法+动态规划

一.贪心算法

1.分饼干问题

#思路:排序加贪心 先让胃口小的孩子满足
class Solution:def findContentChildren(self, g, s):print('==g:', g)print('==s:', s)g = sorted(g)#孩子s = sorted(s)#饼干res = 0for j in range(len(s)):#遍历饼干　先给胃口小的分配if res<len(g):if g[res]<=s[j]:res+=1print('==res:', res)return resg = [1,2]
s = [1,2,3]
# g = [1, 2, 3]
# s = [1, 1]
sol = Solution()
sol.findContentChildren(g, s)

2.钱币找零问题

用最少的纸币来支付同等的金钱。

class Solution:def coinChange_2(self, coins, amount):coins=sorted(coins,reverse=True)print(coins)five_number=0two_number=0one_number=0while amount>=coins[0]:five_number+=1amount-=coins[0]# print('five_number:',five_number)# print(amount)while amount>=coins[1]:two_number+=1amount-=coins[1]# print('two__number:',two_number)# print(amount)while amount>=coins[-1]:one_number+=1amount-=coins[-1]# print('one__number:',one_number)# print(amount)return five_number,two_number,one_number
coins = [1, 2, 5]
amount = 11
sol = Solution()
five_number,two_number,one_number = sol.coinChange_2(coins, amount)
print('five_number:',five_number)
print('two_number:',two_number)
print('one_number:',one_number)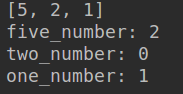

3.区间覆盖

假设我们有 n 个区间，区间的起始端点和结束端点分别是 [l1, r1]，[l2, r2]，[l3, r3]，……，[...

我们从这 n 个区间中选出一部分区间，这部分区间满足两两不相交，端点相交不算，最多有多少区间;

这个问题主要在于右端点选小的，使右边能够有更大的区间覆盖。

4,霍夫曼编码(用于数据压缩)

假设1000个字符，每个字符占一个1个byte，一个byte=8bits，那么存储这1000个就要8000bits，怎么节省呢？

发现这1000个字符只有a,b,c,d,e,f六种不同的字符，所以可以用三个二进制来表示，这样空间就压缩到了3000bits,

根据贪心算法，出现字符频率次数多的，用稍微短的编码，而出现字符频率次数少的，用稍微长的编码，

例题1：

N = int(input())
line = []
for i in range(N):a, b = sorted(list(map(int, input().split(' '))))line.append([a, b])
print(line)# line=[[3, 6], [1, 3], [2, 5]]
line = sorted(line, key=lambda x: x[1])
print('line=', line)ret = [line[0]]
print('ret=', ret)
for item in line[1:]:print('item=', item)if ret[-1][1] > item[0]:passelse:ret.append(item)
print(ret)
print(len(ret))

例题2：假设小偷有一个背包，最多能装20公斤赃物，他闯入一户人家，发现如下表所示的物品。很显然，他不能把所有物品都装进背包，所以必须确定拿走哪些物品，留下哪些物品。

名称	价格（美元）	重量（kg）
电脑	200	20
收音机	20	4
钟	175	10
花瓶	50	2
书	10	1
油画	90	9

class Thing(object):"""物品"""def __init__(self, name, price, weight):self.name = nameself.price = priceself.weight = weight@propertydef value(self):"""价格重量比"""return self.price / self.weightdef input_thing():"""输入物品信息"""name_str, price_str, weight_str = input().split()return name_str, int(price_str), int(weight_str)###贪心算法 根据单位价值进行选择
# a 200 20
# b 20 4
# c 175 10
# d 50 2
# e 10 1
# f 90 9
def main():max_weight, num_of_things = map(int, input().split())# max_weight, num_of_things=20,6print('max_weight',max_weight)print('num_of_things',num_of_things)all_things = []for _ in range(num_of_things):all_things.append(Thing(*input_thing()))#根据价值排序all_things.sort(key=lambda x: x.value, reverse=True)print(all_things[0].name)print(all_things[0].price)print(all_things[0].weight)total_weight = 0total_price = 0choice_thing=[]for thing in all_things:if total_weight + thing.weight <= max_weight:total_weight+=thing.weighttotal_price += thing.pricechoice_thing.append(thing)print('总价值=',total_price)print('偷走的物品是')for i in choice_thing:print(i.name,i.price,i.weight)if __name__ == '__main__':main()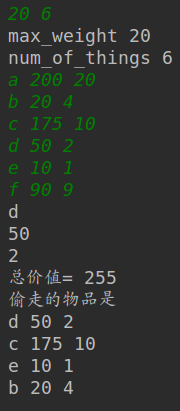

二.回溯算法

《蝴蝶效应》，讲的就是主人公为了达到自己的目标，一直通过回溯的方法，回到童年，在关键的岔路口，重新做选择。

背包总的承载重量是 Ckg。现在我们有 n 个物品，每个物品的重量不一样，并且不能分割，选哪几种才能让背包的总重量最大，且背包不会坏。

bestV = 0
curW = 0
curV = 0
bestx = Nonedef backtrack(i):global bestV, curW, curV, x, bestxif i >= n:if bestV < curV:bestV = curVbestx = x[:]else:if curW + w[i] <= c:x[i] = TruecurW += w[i]curV += v[i]backtrack(i + 1)curW -= w[i]curV -= v[i]x[i] = Falsebacktrack(i + 1)if __name__ == '__main__':#实现选择最大价值的物品，且背包不会坏n = 5  #5个物品c = 10 #背包最大承重w = [2, 2, 6, 5, 4] #每个物品重量v = [6, 3, 5, 4, 6] #每个物品价值x = [False for i in range(n)]backtrack(0)print(bestV)print(bestx)

2.电话号码的字母组合

https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-xiang-jie-by-labuladong-2/


class Solution:def backtrace(self, digits, track):if len(digits) == 0:#满足终止条件self.res.append(track)returnfor letter in self.phone[digits[0]]:#　for循环去遍历选择条件store = track#保存中间结果用于回溯track += letterself.backtrace(digits[1:], track)track = store#恢复中间结果回溯def letterCombinations(self, digits):self.res = []if len(digits) == 0:return self.resself.phone = {'2': ['a', 'b', 'c'],'3': ['d', 'e', 'f'],'4': ['g', 'h', 'i'],'5': ['j', 'k', 'l'],'6': ['m', 'n', 'o'],'7': ['p', 'q', 'r', 's'],'8': ['t', 'u', 'v'],'9': ['w', 'x', 'y', 'z']}self.backtrace(digits, track='')print('==self.res:', self.res)return self.resdigits = "23"
sol = Solution()
sol.letterCombinations(digits)

3.递归实现全排列:

含有三种解法

def swap(a, p, i):a[p], a[i] = a[i], a[p]return a#取第一个数,剩下的做排序,边界条件是开始索引p==终止索引q
def main(a, p, q):res = []def permute(a, p, q):if p == q:res.append(a.copy())print('res:', res)else:for i in range(p, q, 1):swap(a, p, i)permute(a, p+1, q)print('a:', a.copy())swap(a, p, i)#a还原成原顺序,比如2开头的结束了是2 1 3 需要还原成1 2 3 在吧3放在开头在排序print('==a:', a.copy())permute(a, p, q)print('==res:', res)#
# a = [1]
# a = [1, 2]
a=[1, 2, 3]
main(a, 0, len(a))class Solution:def permute(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""def backtrack(first=0):# 所有数都填完了if first == n:res.append(nums.copy())for i in range(first, n):# 动态维护数组nums[first], nums[i] = nums[i], nums[first]# 继续递归填下一个数backtrack(first + 1)# 撤销操作nums[first], nums[i] = nums[i], nums[first]n = len(nums)res = []backtrack()return resa = [1, 2, 3]
sol = Solution()
res = sol.permute(a)
print('===res:', res)

class Solution:def permute(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""n = len(nums)res = []def backtrack(combination, nums):if len(combination) == n:#往前走的数与最早的数长度想等 就是要的结果之一res.append(combination)print('res', res)return# 递归的结束一定 要有returnfor i in range(len(nums)):#递归回溯print('===nums[i]:', nums[i])backtrack(combination+[nums[i]], nums[:i]+nums[i+1:])backtrack([], nums)return resa = [1, 2]
# a = [1, 2, 3]
sol = Solution()
res = sol.permute(a)
print('===res:', res)

4.n皇后问题

#多皇后问题,同一列同一行对角都不能出现同一个皇后

#解法思路：采用回溯算法，可对行进行回溯遍历，用数组记录列，对角索引和，与对角索引差，都不在其中，那么就可以往下走

#终止条件：遍历到的行是最后一行且可以放置

class Solution:def could_place(self, row, col):return not (self.cols_index[col] + self.sub_indexs[row - col] + self.add_indexs[row + col])def place_queen(self, row, col):self.quenes.add((row, col))self.cols_index[col] = 1self.sub_indexs[row - col] = 1self.add_indexs[row + col] = 1def remove_queen(self, row, col):self.quenes.remove((row, col))self.cols_index[col] = 0self.sub_indexs[row - col] = 0self.add_indexs[row + col] = 0def add_res(self):for queue in self.quenes:self.res.append(queue)temp = []for row, col in sorted(self.quenes):temp.append('.'*col + 'Q' + '.' * (self.n - col - 1))self.out.append(temp)def backtrace(self, row):for col in range(self.n):if self.could_place(row, col):self.place_queen(row, col)if (row + 1) == self.n:self.add_res()else:self.backtrace(row + 1)self.remove_queen(row, col)def solveNQueens(self, n: int) -> List[List[str]]:self.n = nself.quenes = set()self.cols_index = [0] * nself.sub_indexs = [0]* (2 * n -1)self.add_indexs = [0]* (2 * n -1)self.res = []self.out = []self.backtrace(row = 0)return self.out

三.动态规划

其是一种空间换时间的算法。

1.递归与动态规划解决最大不相邻数之和

#不相邻最大数 递归解法
def rect_opt(arr,i):if i==0:return arr[i]elif i==1:return max(arr[i-1],arr[i])else:#选自身A=rect_opt(arr,i-2)+arr[i]#不选自身B=rect_opt(arr,i-1)return max(A,B)
arr=[4,1,1,9,1]
arr=[1,2,3,4,5]
res=rect_opt(arr,len(arr)-1)
print('res:',res)#不相邻最大数 DP解法
def dp_opt(arr):opt=[0]*len(arr)opt[0]=arr[0]opt[1]=max(arr[0],arr[1])for i in range(2,len(arr)):opt[i]=max(opt[i-2]+arr[i],opt[i-1])return optarr=[4,1,1,9,1]
arr=[1,2,3,4,5]
opt=dp_opt(arr)
print('opt:',opt)
print('res:',opt[-1])

2.动态规划解决最大公共子串问题

# # 动态规划解决最大公共子串问题
def find_lcsubstr(s1, s2):m = [[0 for i in range(len(s2) + 1)] for j in range(len(s1) + 1)]  # 生成0矩阵，为方便后续计算，比字符串长度多了一列print(m)mmax = 0  # 最长匹配的长度p = 0  # 最长匹配对应在si中的最后一位for i in range(len(s1)):for j in range(len(s2)):if s1[i] == s2[j]:m[i + 1][j + 1] = m[i][j] + 1if m[i + 1][j + 1] > mmax:mmax = m[i + 1][j + 1]p = i + 1print(p)return s1[(p - mmax):p], mmax  # 返回最长子串及其长度

3. 动态规划解决最大公共子序列问题

方法1:

import numpy as np
def find_lcseque(s1, s2):# 生成字符串长度加1的0矩阵，m用来保存对应位置匹配的结果m = [[0 for x in range(len(s2) + 1)] for y in range(len(s1) + 1)]print(m)# d用来记录转移方向d = [[None for x in range(len(s2) + 1)] for y in range(len(s1) + 1)]print(d)for i in range(len(s1)):for j in range(len(s2)):if s1[i] == s2[j]:  # 字符匹配成功，则该位置的值为左上方的值加1m[i + 1][j + 1] = m[i][j] + 1d[i + 1][j + 1] = 'ok'elif m[i + 1][j] > m[i][j + 1]:  # 左值大于上值，则该位置的值为左值，并标记回溯时的方向m[i + 1][j + 1] = m[i + 1][j]d[i + 1][j + 1] = 'left'else:  # 上值大于左值，则该位置的值为上值，并标记方向upm[i + 1][j + 1] = m[i][j + 1]d[i + 1][j + 1] = 'up'print(m)print(d)(i, j) = (len(s1), len(s2))print(np.array(d))s = []while m[i][j]:  # m[i][j]不为0 说明是存在公共子序列c = d[i][j]if c == 'ok':  # 匹配成功，插入该字符，并向左上角找下一个s.append(s1[i - 1])i -= 1j -= 1if c == 'left':  # 根据标记，向左找下一个j -= 1if c == 'up':  # 根据标记，向上找下一个i -= 1s.reverse()return ''.join(s)res=find_lcseque('vesista', 'vsiss')print(res)

方法2:

import numpy as npclass Solution(object):def longestCommonSubsequence(self, text1, text2):""":type text1: str:type text2: str:rtype: int"""matrix = [[0 for i in range(len(text2) + 1)] for j in range(len(text1) + 1)]# print('==matrix:', matrix)ok_matrix = [[0 for i in range(len(text2) + 1)] for j in range(len(text1) + 1)]res = ''value = 0record_i_j = []for i in range(len(text1)):for j in range(len(text2)):if text1[i] == text2[j]:  # 找到相等的字符matrix[i + 1][j + 1] = matrix[i][j] + 1if matrix[i+1][j+1] > value:#递增的地方 才记录value = matrix[i+1][j+1]ok_matrix[i][j] = 1else:matrix[i + 1][j + 1] = max(matrix[i + 1][j], matrix[i][j + 1])print('==matrix:', np.array(matrix))print(np.array(ok_matrix))for i in range(len(ok_matrix)):for j in range(len(ok_matrix[0])):if ok_matrix[i][j] == 1:print('===i,j', i, j)res += text1[i]print('===res:', res)return len(res)sol = Solution()
# text1 = "abcde"
# text2 = "ace"
text1 = "ezupkr"
text2 = "ubmrapg"
# text1 = "bsbininm"
# text2 ="jmjkbkjkv"
# text1 = "abcba"
# text2 = "abcbcba"
# text1 = "oxcpqrsvwf"
# text2 = "shmtulqrypy"
res = sol.longestCommonSubsequence(text1, text2)

只要求长度:

class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:n = len(text1)m = len(text2)dp = [[0 for _ in range(m + 1)] for _ in range(n + 1)]for i in range(n):for j in range(m):if text1[i] == text2[j]:dp[i + 1][j + 1] = dp[i][j] + 1else:dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1])return dp[-1][-1]

c++实现:

class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int n = text1.size();int m = text2.size();vector<vector<int> > dp(n + 1, vector<int>(m + 1, 0));for(int i = 0; i < n; i++){for(int j = 0; j < m; j++){if(text1[i] == text2[j]){dp[i+1][j+1] = dp[i][j] + 1;}else{dp[i+1][j+1] = max(dp[i+1][j], dp[i][j+1]);}}}return dp[n][m];}
};

4.求解矩阵最短路径

原始矩阵：

状态转移矩阵：

代码：

import numpy as np
class Solution(object):def minPathSum(self, grid):""":type grid: List[List[int]]:rtype: int"""rows=len(grid)cols=len(grid[0])opt=[[0 for i in range(cols)] for i in range(rows)]# print(np.array(opt))opt[0][0] = grid[0][0]for j in range(1,cols):opt[0][j]=opt[0][j-1]+grid[0][j]# print(np.array(opt))for i in range(1,rows):opt[i][0]=opt[i-1][0]+grid[i][0]# print(np.array(opt))for i in range(1,rows):for j in range(1,cols):opt[i][j]=min(opt[i-1][j]+grid[i][j],opt[i][j-1]+grid[i][j])# print(np.array(opt))return np.array(opt)
grid=[[1,3,1],[1,5,1],[4,2,1]]
sol=Solution()
res=sol.minPathSum(grid)
print('res:')
print(res)
print(res[-1][-1])

结果：

5.子列表元素之和的最大值

解法1.

class Solution(object):def maxSubArray(self, arr):""":type nums: List[int]:rtype: int"""temp = len(arr) * [0]temp[0] = max(arr[0], 0)opt = len(arr)*[0]opt[0]=max(arr[0],0)for i in range(1,len(arr)):temp[i] = max(temp[i - 1]+arr[i], arr[i])opt[i] = max(temp[i],opt[i-1])print('temp:',temp)return optarr=[1, -2, 3, 5, -3, 2]
sol=Solution()
res=sol.maxSubArray(arr)
print('res:',res)

解法2.

class Solution(object):def maxSubArray(self, nums):""":type nums: List[int]:rtype: int"""for i in range(1,len(nums)):nums[i]+=max(nums[i-1],0)return numsa=[1, -2, 3, 5, -3, 2]
sol=Solution()
res=sol.maxSubArray(a)
print('res:',res)

6-1. 01背包问题

（1）.复杂解法，空间复杂度为O(N*W)

dp[i][j]:表示第i件物品，重量为j的价值

不选i: dp[i][j] = dp[i-1][j]

选i: dp[i][j] = dp[i-1][j-w[i]]+v[i]


"""
物品的数量，
N = 6
书包能承受的重量，
W = 10
每个物品的重量，
things_w = [2, 2, 3, 1, 5, 2]
每个物品的价值
things_v = [2, 3, 1, 5, 4, 3]
"""
N = 6
W = 10
things_w = [2, 2, 3, 1, 5, 2]
things_v = [2, 3, 1, 5, 4, 3]# import numpy as np
#
def bag_complicate(N, W, things_w, things_v):dp = [[0 for j in range(W + 1)] for i in range(N)]print('==np.array(dp):', np.array(dp))for j in range(W + 1):if j >= things_w[0]:dp[0][j] = things_v[0]print('==np.array(dp):', np.array(dp))for i in range(1, N):for j in range(W + 1):dp[i][j] = dp[i - 1][j]  # 不选if j >= things_w[i]:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - things_w[i]] + things_v[i])print('==np.array(dp):\n', np.array(dp))return dpdef show(N, W, things_w, value):print('最大价值为:', value[N - 1][W])x = [False for i in range(N)]j = Wfor i in range(N - 1, 0, -1):if value[i][j] > value[i - 1][j]:x[i] = Truej -= things_w[i]print('x', x)# print('背包中所装物品为:')# for i in range(numbers):print('==np.array(dp):', np.array(dp))#     if x[i]:#         print('第', i+1, '个,', end='')if __name__ == '__main__':dp = bag_complicate(N, W, things_w, things_v)show(N, W, things_w, dp)

（2）. 简单解法，空间复杂度为O(Ｗ)

思路：

不选i: dp[j] = dp[j]

选i: dp[j] = dp[j-w[i]]+v[i]

要注意的是重量需要逆序遍历，因为如果采用正序的话 dp[j -ｗ[i]]会被之前的操作更新为新值


N = 6
W = 10
things_w = [2, 2, 3, 1, 5, 2]
things_v = [2, 3, 1, 5, 4, 3]def bag_easy(N,W,things_w,things_v):dp = [0 for i in range(W+1)]print('==dp:', dp)for i in range(N):for j in range(W, 0, -1):#记得用一维空间要逆序　防止if j >= things_w[i]:dp[j] = max(dp[j-things_w[i]]+things_v[i], dp[j])print('==dp:', dp)return dpbag_easy(N,W,things_w,things_v)

6-2.完全背包问题

(1)复杂解法

dp[i][j]:表示第i件物品，重量为j的价值

不选i: dp[i][j] = dp[i-1][j]

选i: dp[i][j] = dp[i][j-w[i]]+v[i]


"""
物品的数量，
N = 6
书包能承受的重量，
W = 10
每个物品的重量，
things_w = [2, 2, 3, 1, 5, 2]
每个物品的价值
things_v = [2, 3, 1, 5, 4, 3]
"""
N = 6
W = 10
things_w = [2, 2, 3, 1, 5, 2]
things_v = [2, 3, 1, 5, 4, 3]# import numpy as np
#
def bag_complicate(N, W, things_w, things_v):dp = [[0 for j in range(W + 1)] for i in range(N)]print('==np.array(dp):', np.array(dp))for j in range(W + 1):if j >= things_w[0]:dp[0][j] = things_v[0]print('==np.array(dp):', np.array(dp))for i in range(1, N):for j in range(W + 1):dp[i][j] = dp[i - 1][j]  # 不选if j >= things_w[i]:dp[i][j] = max(dp[i - 1][j], dp[i][j - things_w[i]] + things_v[i])print('==np.array(dp):\n', np.array(dp))print('最大价值为:', dp[N - 1][W])return dpif __name__ == '__main__':dp = bag_complicate(N, W, things_w, things_v)

(2)优化解法

def bag_easy(N,W,things_w,things_v):dp = [i for i in range(W+1)]print('==np.array(dp):', np.array(dp))for i in range(N):for j in range(W+1):if j >= things_w[i]:dp[j] = max(dp[j], dp[j-things_w[i]]+things_v[i])else:dp[j] = dp[j]print('==np.array(dp):', np.array(dp))
if __name__ == '__main__':bag_easy(N, W, things_w, things_v)

7.零钱兑换

https://leetcode-cn.com/problems/coin-change/submissions/

给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。假设我们取面额为 1 的硬币，那么接下来需要凑齐的总金额变为 11 - 1 = 10，即 f(11) = f(10) + 1，这里的 +1 就是我们取出的面额为 1 的硬币。

同理，如果取面额为 2 或面额为 5 的硬币可以得到：

f(11) = f(9) + 1
f(11) = f(6) + 1

所以：

f(11) = min(f(10), f(9), f(6)) + 1

class Solution:def coinChange(self, coins,amount):f = [float("inf")] * (amount + 1)f[0] = 0for i in range(1, amount + 1):for coin in coins:if i - coin >= 0:f[i] = min(f[i], f[i - coin]+1)print(f)return f[-1] if f[-1] != float("inf") else -1coins = [1, 2, 5]
amount = 11
sol=Solution()
res=sol.coinChange(coins,amount)
print('res:')
print(res)

8.乘积最大子序列

乘法与加法最大差别在于，当前元素的符号具有全局性的作用。如果当前元素为负，那么连乘到上个元素的最大乘积，再乘以当前元素，就变成负数，甚至可能成为最小乘积。同样，连乘到上个元素的最小乘积如为负，再乘以当前元素，就变成正数，甚至可能成为最大乘积，所以用两个列表存储当前最大最小值。

class Solution(object):def maxProduct(self, nums):""":type nums: List[int]:rtype: int"""if len(nums)<=1:return Noneopt_min=[0]*len(nums)opt_max = [0] * len(nums)opt_min[0]=nums[0]opt_max[0] = nums[0]for i in range(1,len(nums)):opt_min[i] = min(min(opt_min[i-1]*nums[i],opt_max[i-1]*nums[i]),nums[i])opt_max[i] = max(max(opt_min[i-1]*nums[i],opt_max[i-1]*nums[i]),nums[i])print('opt_min',opt_min)print('opt_max',opt_max)return max(opt_max)nums = [2, 3, -4,4]
# nums =[-2,0,-1]
# nums=[0,2]
# amount = 11
sol=Solution()
res=sol.maxProduct(nums)
print('res:')
print(res)

9.三角形最小路径和

https://leetcode-cn.com/problems/triangle/submissions/

class Solution(object):def minimumTotal(self, triangle):""":type triangle: List[List[int]]:rtype: int"""# res=[]for i in range(1,len(triangle)):for j in range(len(triangle[i])):#边界条件if j == 0:triangle[i][j]=triangle[i-1][j]+triangle[i][j]# 边界条件elif j == i:triangle[i][j] = triangle[i - 1][j-1] + triangle[i][j]else:triangle[i][j] = min(triangle[i - 1][j - 1],triangle[i-1][j]) + triangle[i][j]return min(triangle[-1])triangle =[[2],[3,4],[6,5,7],[4,1,8,3]
]
# nums =[-2,0,-1]
# nums=[0,2]
# amount = 11
sol=Solution()
res=sol.minimumTotal(triangle)
print('res:')
print(res)

10.收益最大--简易

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/submissions/

前i天的最大收益 = max{前i-1天的最大收益，第i天的价格-前i-1天中的最小价格}

class Solution(object):def maxProfit(self, prices):""":type prices: List[int]:rtype: int"""if len(prices)<=1:return Noneopt=[0]*len(prices)min_p=9999for i in range(len(prices)):#记录第i天之前的最小价min_p = min(min_p, prices[i])opt[i] = max(opt[i-1],prices[i]-min_p)#min(prices[:i]))print(opt)return opt[-1]prices =[1,2]
# nums =[-2,0,-1]
# nums=[0,2]
# amount = 11
sol=Solution()
res=sol.maxProfit(prices)
print('res:')
print(res)

10.收益最大--中级

https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/

# sell[i]表示截至第i天，最后一个操作是卖时的最大收益；
# buy[i]表示截至第i天，最后一个操作是买时的最大收益；
# cool[i]表示截至第i天，最后一个操作是冷冻期时的最大收益；
class Solution(object):def maxProfit(self, prices):""":type prices: List[int]:rtype: int"""if len(prices) == 0:return 0sell = [0]*len(prices)buy = [0] * len(prices)cool = [0] * len(prices)buy[0]-=prices[0]print(buy)for i in range(1,len(prices)):#           第i天卖    第i天不卖sell[i]=max(sell[i-1],buy[i-1]+prices[i])#           第i天不买    第i天买buy[i] = max(buy[i-1],cool[i-1]-prices[i])#           第i天冷                  第i天不冷cool[i] = max(sell[i-1],cool[i - 1],buy[i-1])print(buy)print(cool)print(sell)return sell[-1]prices=[1,2,3,0,2]
sol = Solution()
res = sol.maxProfit(prices)
print('res:')
print(res)

11.矩阵走法最多路径

https://leetcode-cn.com/problems/unique-paths/

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

class Solution(object):def uniquePaths(self, m, n):""":type m: int:type n: int:rtype: int"""opt=[[0 for i in range(n)] for j in range(m)]print(opt)for i in range(m):for j in range(n):if i==0 or j==0:opt[i][j]=1else:opt[i][j]=opt[i-1][j]+opt[i][j-1]print(opt)print(opt[-1][-1])return opt[-1][-1]m = 3
n = 2
sol=Solution()
sol.uniquePaths(m,n)

12.一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径

https://leetcode-cn.com/problems/unique-paths-ii/

class Solution(object):def uniquePathsWithObstacles(self, obstacleGrid):""":type obstacleGrid: List[List[int]]:rtype: int"""opt=[[0 for i in range(len(obstacleGrid[0]))] for j in range(len(obstacleGrid))]# print(opt)for i in range(len(obstacleGrid)):for j in range(len(obstacleGrid[0])):#边界条件if obstacleGrid[i][j]==1:opt[i][j]=0else:if i==0 and j==0:opt[i][j]=1elif  i==0:opt[i][j]=opt[i][j-1]elif j==0:opt[i][j] = opt[i-1][j]else:opt[i][j]=opt[i-1][j]+opt[i][j-1]# print(opt)return opt[-1][-1]

13.输入: s = "leetcode", wordDict = ["leet", "code"] 输出: true

https://leetcode-cn.com/problems/word-break/

class Solution(object):def wordBreak(self, s, wordDict):""":type s: str:type wordDict: List[str]:rtype: bool"""word_set = {word for word in wordDict}# print(word_set)dp = [False for _ in range(len(s))]dp[0] = s[0] in word_set#第一层循环最外层for i in range(1, len(s)):if s[:i+1] in wordDict:dp[i] = True#内层循环for j in range(i):if dp[j] and s[j+1:i+1] in wordDict:dp[i] = Truebreakprint(dp)return dp[-1]s = "leetcode"
wordDict = ["leet", "code"]
sol=Solution()
res=sol.wordBreak(s,wordDict)

14,最大正方形面积

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

https://leetcode-cn.com/problems/maximal-square/

class Solution(object):def maximalSquare(self, matrix):""":type matrix: List[List[str]]:rtype: int"""if not matrix:return 0rows=len(matrix)columns=len(matrix[0])dp=[[0]*columns for i in range(rows)]#边界条件dp[0]=list(map(int,matrix[0]))for i in range(rows):dp[i][0] = int(matrix[i][0])for i in range(1,rows):for j in range(1,columns):#递归条件if matrix[i][j]=="1":dp[i][j]=min(dp[i-1][j],dp[i-1][j-1],dp[i][j-1])+1res=0for i in range(rows):for j in range(columns):res = max(res,dp[i][j]**2)print('dp:',dp)print(res)return res# matrix=[[1, 0, 1, 0, 0],
#         [1, 0, 1, 1, 1],
#         [1, 1, 1, 1, 1],
#         [1, 0, 0, 1, 0]]
matrix=[["1"]]
sol=Solution()
res=sol.maximalSquare(matrix)
print('res:',res)

15.将列表中相邻的数聚类在一起(动态规划)

1直接相邻就聚，带来的问题是如果值依次增加，会不准（动态规划）

a=[1,2,3,4,56,34,46,100,110,123]
a=sorted(a)
print('a:',a)
opt=[0]*len(a)
for i in range(1,len(a)):if a[i]-a[i-1]<20:opt[i]=1
opt.append(0)
print('opt:',opt)
index=[j for j in range(len(opt)) if opt[j]==0]
print('index:',index)
for k in range(len(index)-1):print(a[index[k]:index[k+1]])

2.优化版，双指针

a = [1, 2, 3, 4, 56, 34, 46, 100, 110, 123]
a = sorted(a)
print('a:', a)
res = []
left, right = 0, 0
while right <len(a):right= left+1while right < len(a) and a[right]-a[left]<20:right+=1res.append([left, right-1])left = rightprint('==res:', res)for i in res:print('==a[i[0]:i[1]]:', a[i[0]:i[1] + 1])

16.打家劫舍简单版房屋一排

https://leetcode-cn.com/problems/house-robber/

class Solution(object):def rob(self, nums):""":type nums: List[int]:rtype: int"""if len(nums)==0:return 0if len(nums)<=2:return max(nums)opt = [0] * len(nums)opt[0] = nums[0]opt[1] = max(nums[:2])#注意边界条件 从2开始 所以要对 0 1 赋值for i in range(2,len(nums)):opt[i]=max(opt[i-2]+nums[i],opt[i-1])print(opt)return opt[-1]
nums=[1,2,3,1]
sol = Solution()
res = sol.rob(nums)
print('res:')
print(res)

17.打家劫舍中等版房屋围成圈所以分为不抢第一家和不抢最后一家两种情况

https://leetcode-cn.com/problems/house-robber-ii/

class Solution(object):def rob(self, nums):""":type nums: List[int]:rtype: int"""if len(nums)==0:return 0if len(nums)<=2:return max(nums)opt1 = [0] * len(nums)opt2 = [0] * len(nums)#不抢第一家opt1[0] = 0opt1[1] = nums[1]#不抢最后一家opt2[0] = nums[0]opt2[1] = max(nums[:2])for i in range(2,len(nums)):opt1[i]=max(opt1[i-2]+nums[i], opt1[i-1])print(opt1)for i in range(2, len(nums)-1):opt2[i] = max(opt2[i - 2] + nums[i], opt2[i - 1])print(opt2)return max(opt1[-1],opt2[-2])
nums=[1,2,3,1]
sol = Solution()
res = sol.rob(nums)
print('res:')
print(res)

18.最长上升子序列

给定一个无序的整数数组，找到其中最长上升子序列的长度。

利用opt列表来存储在第i个元素之前小于i的最长长度。

class Solution(object):def lengthOfLIS(self, nums):""":type nums: List[int]:rtype: int"""if nums==[]:return 0opt=[0]*len(nums)opt[0]=1for i in range(len(nums)):max_value = 0for j in range(i):#在<i这段内 找出小于nums[i]的数字if nums[i]>nums[j]:max_value=max(max_value,opt[j])opt[i]=max_value+1# print(opt)# print(max_value)return max(opt)

１９．编辑距离计算字符之间相似度

编辑距离，又称Levenshtein距离（莱文斯坦距离也叫做Edit Distance），是指两个字串之间，由一个转成另一个所需的最少编辑操作次数，如果它们的距离越大，说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符，插入一个字符，删除一个字符。

mat[i+1,j]+1表示增加操作
d[i,j+1]+1 表示删除操作
d[i,j]+temp表示替换操作,其中temp取0或1

import os
import numpy as np
def edit_distance(S1,S2):#S1列　S2行mat = [[0] *(len(S1)+1) for i in range(len(S2)+1)]# print('mat:', mat)for i in range(len(S2)):mat[i+1][0] = mat[i][0]+1# print('mat:', mat)for i in range(len(S1)):mat[0][i+1] = mat[0][i]+1print('mat:\n', np.array(mat))#相等就为０　不想等加１for i in range(len(S2)):for j in range(len(S1)):if S2[i] == S1[j]:print('S2[i]:', S2[i])mat[i + 1][j + 1] = min(mat[i][j] + 0, mat[i + 1][j]+1, mat[i][j + 1]+1)else:mat[i + 1][j + 1] = min(mat[i][j] + 1, mat[i + 1][j]+1, mat[i][j + 1]+1)print('mat:\n', np.array(mat))dis = mat[-1][-1]print('dis:', dis)return dis
# S1 = 'iva1'
# S2 = 'iva'S2 = '者記聞新'
S1 = '浪(第'
dis = edit_distance(S1, S2)
similarity = 1. - dis/max(len(S1), len(S2))
print('similarity:', similarity)