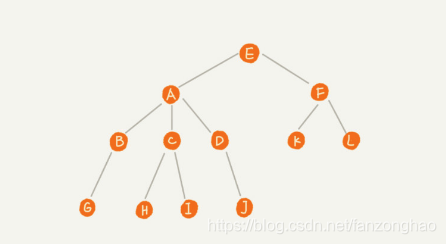
一,树
E为根节点,BCD互称为兄弟节点,G、H、I、J、K、L互称为叶子节点(没有子节点)
树的高度,深度,层数.

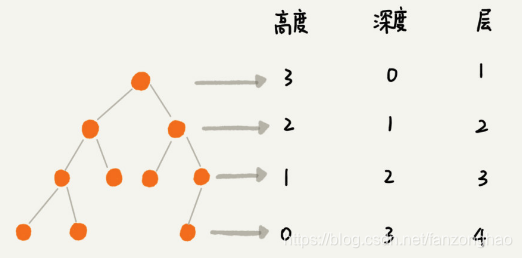
高度从下往上数(0开始),深度从上往下数(0开始).
二,二叉树
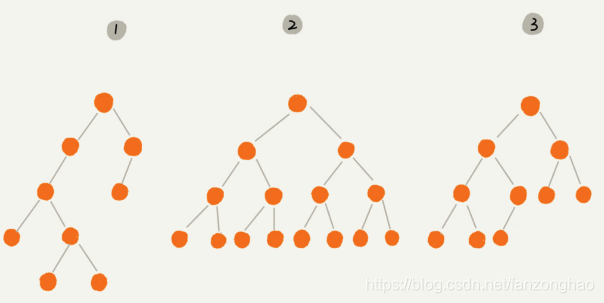
2为满二叉树,二叉树中除了叶子结点,每个结点的度都为 2.
3为完全二叉树,如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布
# 实现一个二叉树
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Noneself.nexts = []root_node = TreeNode(1)
node_2 = TreeNode(2)
node_3 = TreeNode(3)
node_4 = TreeNode(4)
node_5 = TreeNode(5)
node_6 = TreeNode(6)
node_7 = TreeNode(7)
node_8 = TreeNode(8)
node_9 = TreeNode(9)
node_10 = TreeNode(10)def littleTree(root, left, right):root.left = leftroot.right = rightif root.left:root.nexts.append(root.left)if root.right:root.nexts.append(root.right)# print(root.left)# print(root.right)# print(root.nexts)littleTree(root_node, node_2, node_3)
littleTree(node_2, node_4, node_5)
littleTree(node_5, node_10, None)
print('===root_node:', root_node.left)
print('===root_node:', root_node.right)
print('===root_node:', root_node.nexts)
print('===root_node.left.left:', root_node.left.left)
print('===root_node.left.right:', root_node.left.right)
print('===root_node.left.nexts:', root_node.left.nexts)
三,存储二叉树
3.1链式存储
大部分二叉树采用这种结果存储.
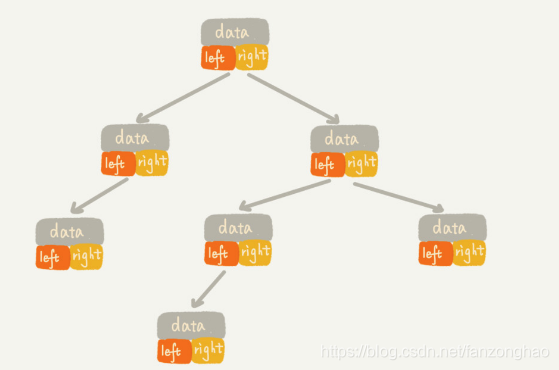
每个节点有三个字段,其中一个存储数据,另外两个是指向左右子节的指针.
3.2顺序存储
根节点存储在i=1,左子节点存储在2*i,右子节点存储在2*i+1
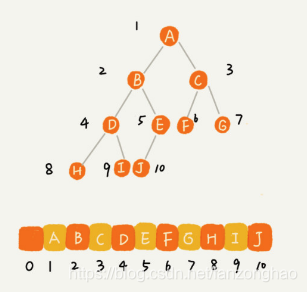
由上可看出,对于完全二叉树,顺序存储相比链式存储节约空间,其他的话就浪费空间了.
四,二叉树遍历
4.1前序遍历
对树中的任意节点,先打印节点,在打印左子树,最后打印右子树.
对于根节点开始:
先遍历根节点;
随后递归地遍历左子树;
最后递归地遍历右子树。
4.2中序遍历
对树中的任意节点,先打印左子树,在打印节点,最后打印右子树.
先递归地遍历左子树;
随后遍历根节点;
最后递归地遍历右子树。
4.3后序遍历
对树中的任意节点,先打印左子树,在打印右子树,最后打印节点.
先递归地遍历左子树;
最后递归地遍历右子树。
随后遍历根节点;
二叉树前序遍历的顺序为:
二叉树中序遍历的顺序为:
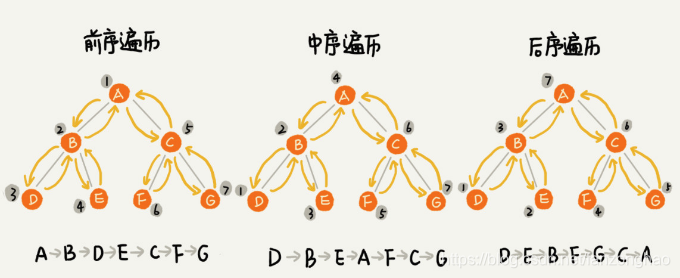
前序遍历的递推公式:
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式:
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式:
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
可看出每个节点最多会被访问两次,所以遍历操作的时间复杂度,跟节点的个数n成正比,时间复杂度是O(n).
例1:二叉树的创建和遍历
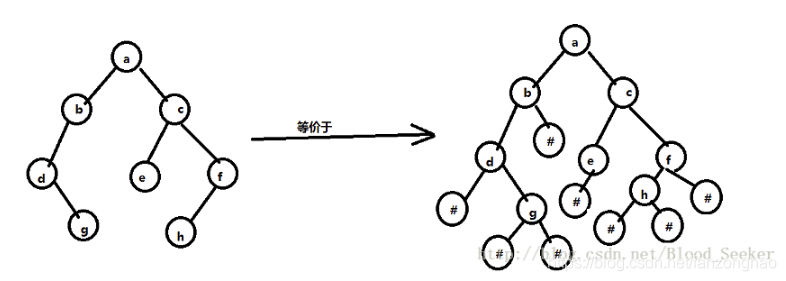
class BTNode(object):def __init__(self, key=None, lchild=None, rchild=None):self.key = keyprint('self.key',self.key)self.lchild = lchildprint('self.lchild',self.lchild)self.rchild = rchildprint('self.rchild',self.rchild)class BiTree(object):def __init__(self, data_list):#初始化即将传入的列表的迭代器self.it = iter(data_list)print('self.it',self.it)def createBiTree(self, bt=None):try:#步进获取下一个元素next_data = next(self.it)print('next_data=',next_data)#如果当前列表元素为'#', 则认为其为 Noneif next_data is "#":bt = Noneelse:bt = BTNode(next_data)bt.lchild = self.createBiTree(bt.lchild)bt.rchild = self.createBiTree(bt.rchild)except Exception as e:print(e)return bt#先序遍历函数def preOrderTrave(self, bt):if bt is not None:print(bt.key, end=" ")self.preOrderTrave(bt.lchild)self.preOrderTrave(bt.rchild)#中序遍历函数def inOrderTrave(self, bt):if bt is not None:self.inOrderTrave(bt.lchild)print(bt.key, end=" ")self.inOrderTrave(bt.rchild)#后序遍历函数def postOrderTrave(self, bt):if bt is not None:self.postOrderTrave(bt.lchild)self.postOrderTrave(bt.rchild)print(bt.key, end=" ")#综合打印def printTrave(self, bt):print("先序遍历: ", end="")self.preOrderTrave(bt)print('\n')print("中序遍历: ", end="")self.inOrderTrave(bt)print('\n')print("后序遍历: ", end="")self.postOrderTrave(bt)print('\n')# data = input("Please input the node value: ")
# data_list = list(data)
data_list=['a', 'b', 'd', '#', 'g', '#', '#', 'c', 'e', '#', '#', 'f', 'h', '#', '#', '#']
print(data_list)
#构建二叉树
btree = BiTree(data_list)
root = btree.createBiTree()btree.printTrave(root)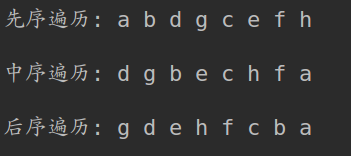
例2:https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/

class BTNode(object):def __init__(self, key=None, lchild=None, rchild=None):self.key = keyprint('self.key',self.key)self.lchild = lchildprint('self.lchild',self.lchild)self.rchild = rchildprint('self.rchild',self.rchild)class BiTree(object):def __init__(self, data_list):#初始化即将传入的列表的迭代器self.it = iter(data_list)print('self.it',self.it)def createBiTree(self, bt=None):try:#步进获取下一个元素next_data = next(self.it)print('next_data=',next_data)#如果当前列表元素为'#', 则认为其为 Noneif next_data is "#":bt = Noneelse:bt = BTNode(next_data)bt.lchild = self.createBiTree(bt.lchild)bt.rchild = self.createBiTree(bt.rchild)except Exception as e:print(e)return bt#先序遍历函数def preOrderTrave(self, bt):if bt is not None:print(bt.key, end=" ")self.preOrderTrave(bt.lchild)self.preOrderTrave(bt.rchild)#中序遍历函数def inOrderTrave(self, bt):if bt is not None:self.inOrderTrave(bt.lchild)print(bt.key, end=" ")self.inOrderTrave(bt.rchild)#后序遍历函数def postOrderTrave(self, bt):if bt is not None:self.postOrderTrave(bt.lchild)self.postOrderTrave(bt.rchild)print(bt.key, end=" ")#综合打印def printTrave(self, bt):print("先序遍历: ", end="")self.preOrderTrave(bt)print('\n')print("中序遍历: ", end="")self.inOrderTrave(bt)print('\n')print("后序遍历: ", end="")self.postOrderTrave(bt)print('\n')def TreeDepth(self, pRoot):# write code hereif pRoot == None:return 0return max(self.TreeDepth(pRoot.lchild), self.TreeDepth(pRoot.rchild)) + 1# data = input("Please input the node value: ")
# data_list = list(data)
# data_list=['a', 'b', 'd', '#', 'g', '#', '#', 'c', 'e', '#', '#', 'f', 'h', '#', '#', '#']
data_list=[3,9,'#','#',20,15,'#','#',7,'#','#']
print(data_list)
#构建二叉树
btree = BiTree(data_list)
root = btree.createBiTree()btree.printTrave(root)res=btree.TreeDepth(root)
print('res',res)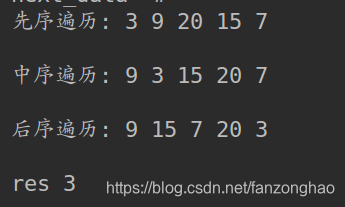
五,二叉查找树
其支持动态数据集合的快速插入、删除、查找操作.
插入、删除、查找操作的时间复杂度也比较稳定,是 O(logn).
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值.
示例如下:
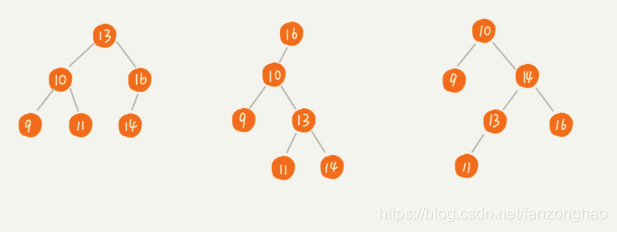
5.1 二叉查找树的查找操作
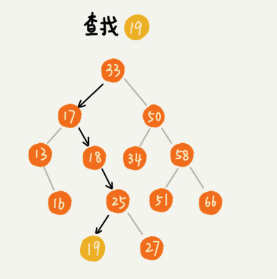
首先,我们看如何在二叉查找树中查找一个节点。我们先取根节点,如果等于就返回,根节点大的话就往左子树查找,否则往右子树查找.
5.2 二叉查找树的插入操作
新插入的数据一般在叶子节点,从根节点开始,比较插入数据和节点的大小关系.
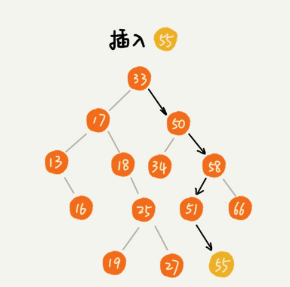
如果插入的数据比节点数据大,并且节点的右子树为空,就将新数据插入到右子树空的位置,如果不为空就继续递归遍历右子树,查找插入位置.插入数据比节点数据小也是同理.
5.3 二叉查找树的删除操作
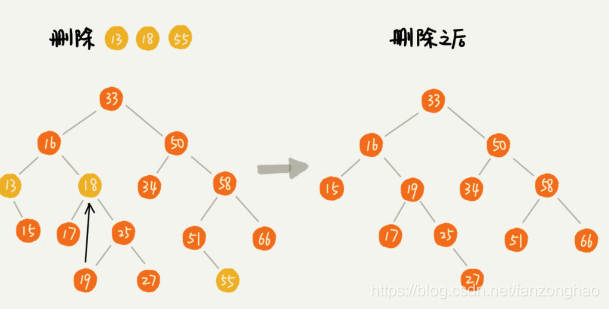
分三种情况:
1.例如55,没有子节点,只需要将父节点中,指向要删除子节点的指针置为null.
2.例如13,只有左子节点或者右子节点,我们只需要更新父节点中指针的指向,16的指针指向15.
3,例如18,有两个节点,需要找到这个节点的右子树最小节点19,把它替换到要删除的节点上,然后再删除这个最小节点19.



















