一.复杂度分析：

可以理解为递归的深度就是空间复杂度，时间复杂度就是O(T*depth),其中Ｔ是每个递归函数的时间复杂度，depth是递归深度．

#空间复杂度O(1)
def sum1_(n):res = 0for i in range(n+1):res+=ireturn res#递归 空间复杂度O(n)
def sum2_(n):if n == 0:return 0return n+sum2_(n-1)res1 = sum1_(n=10)
res2 = sum2_(n=10)
print('==res1:', res1)
print('==res2:', res2)

上式时间复杂度也为O(1*n)=O(n)

二.例子

1.计算x^n:

def pow(x, n):if n==0:return 1.t = pow(x, n//2)if n%2:return x*t*telse:return t*tres = pow(2,3)
print('res:', res)

递归深度:logn ，每个递归函数的时间复杂度为O(1),故时间复杂度为O(logn).

空间复杂度:logn

2.假如这里有 n 个台阶，每次你可以跨 1 个台阶或者 2 个t台阶，请问n个台阶有多少种走法？

第一步走了一个台阶或第一步走了两个台阶，到下一个台阶也是类似，故这是一个递归。

n个台阶就是，走了一个台阶后加剩下n-1台阶的走法，走了两个台阶后剩下n-2台阶的走法，

f(n)=f(n-1)+f(n-2)

终止条件：只剩一个台阶一种走法，只剩两个台阶两种走法，

f(1)=1，f(2)=2

def fun(n):if(n == 1): return 1elif (n == 2): return 2else:return fun(n - 1) + fun(n - 2)

每个递归函数的时间复杂度为O(1)，空间复杂度:O(2^n)， 故时间复杂度为O(2^n).

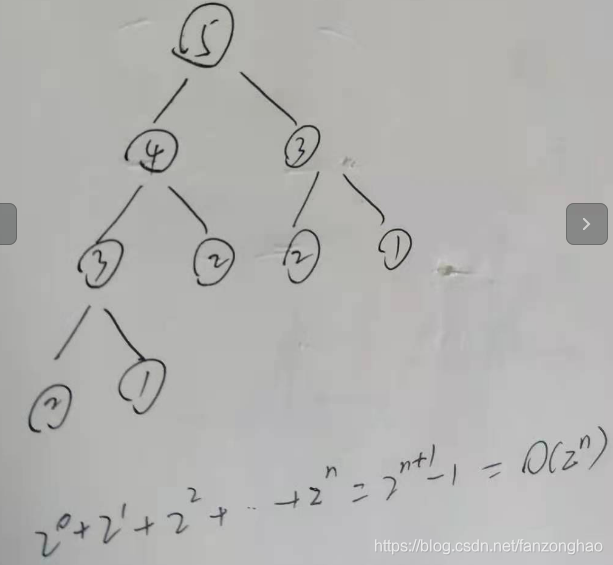
缺点：堆栈溢出、重复计算、函数调用耗时多、空间复杂度高等

防止递归造成堆栈溢出，加入深度，大于1000就不再溢出

depth=0
def fun(n):global depthdepth+=1print('depth=',depth)if (depth>1000): return -1if(n == 1): return 1elif (n == 2): return 2else:return fun(n - 1) + fun(n - 2)
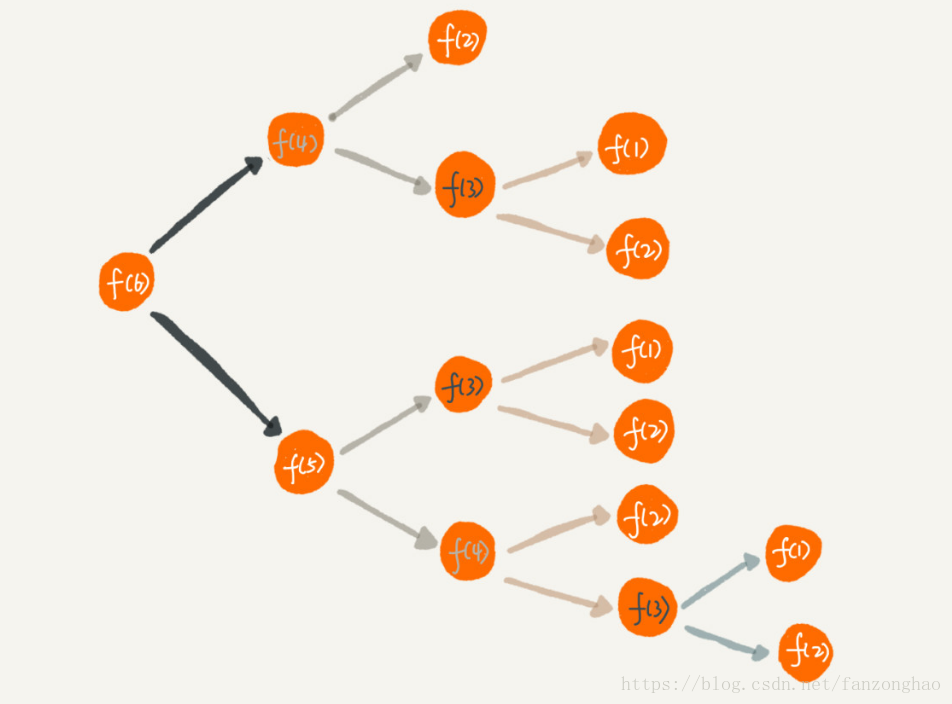
print(fun(3))

存在大量重复计算：

优化思路１：　

递推，从下到上：

class Solution:def numWays(self, n: int) -> int:a,b=1,1for i in range(n):a,b = a+b,areturn b

思路2,将计算过的值存储在进行判断:

def fun(n,arr):if(n == 1): return 1elif (n == 2): return 2else:if arr[n]!=-1:return arr[n]else:arr[n] = fun(n - 1,arr) + fun(n - 2,arr)return arr[n]
n = 6
arr = [-1]*(n+1)
res= fun(n=n, arr=arr)
print('==res:', res)

3.递归实现全排列:

def swap(a, p, i):a[p], a[i] = a[i], a[p]return a#取第一个数,剩下的做排序,边界条件是开始索引p==终止索引q
def main(a, p, q):res = []def permute(a, p, q):if p == q:res.append(a.copy())print('res:', res)else:for i in range(p, q, 1):swap(a, p, i)permute(a, p+1, q)print('a:', a.copy())swap(a, p, i)#a还原成原顺序,比如2开头的结束了是2 1 3 需要还原成1 2 3 在吧3放在开头在排序print('==a:', a.copy())permute(a, p, q)print('==res:', res)#
# a = [1]
# a = [1, 2]
a=[1, 2, 3]
main(a, 0, len(a))class Solution:def permute(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""def backtrack(first=0):# 所有数都填完了if first == n:res.append(nums.copy())for i in range(first, n):# 动态维护数组nums[first], nums[i] = nums[i], nums[first]# 继续递归填下一个数backtrack(first + 1)# 撤销操作nums[first], nums[i] = nums[i], nums[first]n = len(nums)res = []backtrack()return resa = [1, 2, 3]
sol = Solution()
res = sol.permute(a)
print('===res:', res)

4.递归实现快速幂

问题：求 a 的 b 次方对 p 取模的值

#a^b%p
def a_b_p(a,b,p):if b == 0:return 1elif b%2 == 1:#b是奇数return a*a_b_p(a, b-1, p)%pelse:#b是偶数temp = a_b_p(a, b//2, p)return (temp*temp)%pres = a_b_p(3,3,4)
print('==res:', res)

5.递归实现汉罗塔

#include <iostream>
#include <string>
#include <string.h>
#include <stdio.h>
using namespace std;
//a--from b--temp c--to
void hano(int n, char a, char b, char c);
int main(){hano(3, 'a', 'b', 'c');return 0;}
//a--from b--temp c--to
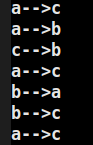
void hano(int n,char a, char b, char c){if(n==1){cout<<a<<"-->"<<c<<endl;}else{hano(n-1, a, c, b);//ｃ为temp,a上面的n-1给bhano(1, a, b, c);//b为temp,a上面的1给chano(n-1, b, a, c);//a为temp,b上面的n-1给c}
}

加上盘子序号:

盘子从上到底是1到n

#include <iostream>
#include <string>
#include <string.h>
#include <stdio.h>
using namespace std;
//a--from b--temp c--to
void hano(int top, int n, char a, char b, char c);
int main(){hano(1, 3, 'a', 'b', 'c');return 0;}
//a--from b--temp c--to
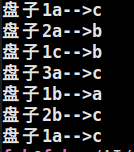
void hano(int top, int n,char a, char b, char c){if(n==1){cout<<"盘子"<<top<<a<<"-->"<<c<<endl;}else{hano(top, n-1, a, c, b);//ｃ为temp,a上面的n-1给bhano(top + n - 1, 1, a, b, c);//b为temp,a上面的1给chano(top, n-1, b, a, c);//a为temp,b上面的n-1给c}
}