二叉树的一些leetcode题目+python(c++)

二叉树考点主要有:

1.三种遍历方式,以及构造二叉树等；

2.求深度,最长直径，最长路径,公共祖先等等;

3.合并二叉树，翻转二叉树，判断平衡性,对称性等;

4.从前序与中序构造二叉树，中序与后序构造二叉树，二叉树序列化等;

5.二叉搜索树

1-1.前序遍历

思路１：递归法 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def helper(self, node):if node is not None:self.res.append(node.val)self.helper(node.left)self.helper(node.right)def preorderTraversal(self, root: TreeNode) -> List[int]:self.res = []self.helper(root)return self.res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> res;void help(TreeNode* node){if(node !=nullptr){res.push_back(node->val);help(node->left);help(node->right);}}vector<int> preorderTraversal(TreeNode* root) {help(root);return res;}
};

思路２栈（迭代法）：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def preorderTraversal(self, root: TreeNode) -> List[int]: res = []if root is None:return resstack = [root]while stack:node = stack.pop()if node:res.append(node.val)stack.append(node.right)stack.append(node.left)return res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> preorderTraversal(TreeNode* root) {vector<int>res;stack<TreeNode*> stack_A;stack_A.push(root);while(stack_A.size()>0){TreeNode* node = stack_A.top();stack_A.pop();if(node){res.push_back(node->val);stack_A.push(node->right);stack_A.push(node->left);}}return res;}
};

1-2.N叉树的前序遍历

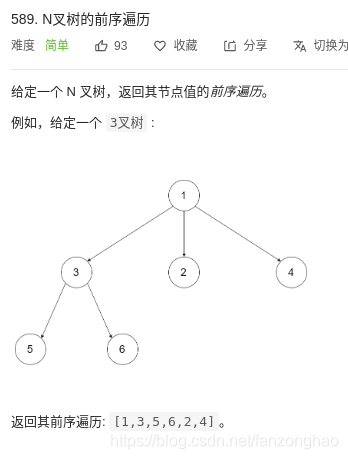
1.递归法 

"""
# Definition for a Node.
class Node:def __init__(self, val=None, children=None):self.val = valself.children = children
"""class Solution:def preorder(self, root: 'Node') -> List[int]:res = []def helper(node):if node:res.append(node.val)for child in node.children:helper(child)helper(root)# print('res:', res)return res

c++实现:

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<int> res;void help(Node* node){if(node!=NULL){res.push_back(node->val);vector<Node* > new_nodes = node->children;for(int i=0;i<new_nodes.size();i++){help(new_nodes[i]);}}}vector<int> preorder(Node* root) {help(root);return res;}
};

2.迭代法 利用栈

"""
# Definition for a Node.
class Node:def __init__(self, val=None, children=None):self.val = valself.children = children
"""class Solution:def preorder(self, root: 'Node') -> List[int]:        res= []if root is None:return resstack = [root]while stack:node = stack.pop()if node:res.append(node.val)stack.extend(node.children[::-1])# print('==res:', res)return res

c++实现:

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/
//后进左子树先出左子树
class Solution {
public:vector<int> preorder(Node* root) {if(root==NULL){return {};}vector<int> res;stack<Node*> stack_A;stack_A.push(root);while (stack_A.size()>0){Node* node = stack_A.top();stack_A.pop();if(node){res.push_back(node->val);vector<Node*> temp_node_list = node->children;for (int i=temp_node_list.size()-1;i>=0;i--){stack_A.push(temp_node_list[i]);}}}return res;}
};

1-3.中序遍历

思路１：递归法 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def helper(self, node):if node is not None:self.helper(node.left)self.res.append(node.val)self.helper(node.right)def inorderTraversal(self, root: TreeNode) -> List[int]:self.res = []self.helper(root)return self.res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int>res;void help(TreeNode* node){if(node){help(node->left);res.push_back(node->val);help(node->right);}}vector<int> inorderTraversal(TreeNode* root) {help(root);return res;}
};

思路2.栈（迭代法）

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):def inorderTraversal(self, root):""":type root: TreeNode:rtype: List[int]"""stack = []node = rootoutput = []if root == None: return outputwhile node or stack:  # 如果node和aStack都是空的，说明全查完了。while node:  # 如果node是空的，说明左边没子节点了。stack.append(node)node = node.leftnode = stack.pop()  # 左边没子节点了就输出栈顶的节点值，然后从它右边的子节点继续。output.append(node.val)node = node.rightreturn output

1-4.后序遍历

思路１：递归 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def helper(self, node):if node:self.helper(node.left)self.helper(node.right)self.res.append(node.val)def postorderTraversal(self, root: TreeNode) -> List[int]:self.res = []self.helper(root)return self.res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> res;void help(TreeNode* node){if(node!=nullptr){help(node->left);help(node->right);res.push_back(node->val);}}vector<int> postorderTraversal(TreeNode* root) {help(root);return res;}
};

 思路２：栈（迭代法）

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def postorderTraversal(self, root: TreeNode) -> List[int]:stack = []res = []prev = Nonewhile root or stack:while root:stack.append(root)root = root.leftroot = stack.pop()if not root.right or root.right == prev:#右子树为空或者为根节点值已经遍历过　prev已经记录右节点的值res.append(root.val)prev = rootroot = Noneelse:stack.append(root)root = root.rightreturn res

1-5.N叉树的后序遍历

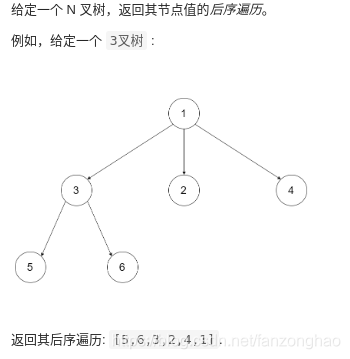
1. 解法1 递归法

#递归法
"""
# Definition for a Node.
class Node:def __init__(self, val=None, children=None):self.val = valself.children = children
"""class Solution:def postorder(self, root: 'Node') -> List[int]:if root is None:return Noneres = []def helper(t):if t is None:returnfor child in t.children:helper(child)res.append(t.val)helper(root)return res

c++实现:

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
public:vector<int> res;void help(Node* node){if(node == NULL){return ;}for(int i=0; i < node->children.size(); i++){help(node->children[i]);}     res.push_back(node->val);       }vector<int> postorder(Node* root) {if (root==NULL){return {};}help(root);return res;}
};

2. 解法2 迭代法

#迭代法
"""
# Definition for a Node.
class Node:def __init__(self, val=None, children=None):self.val = valself.children = children
"""class Solution:def postorder(self, root: 'Node') -> List[int]:if root is None:return Nonestack= [root]res = []while stack:node = stack.pop()res.append(node.val)for child in node.children:stack.append(child)return res[::-1]

1-6.从上到下打印二叉树

1.BFS:思路利用bfs将每一层节点进行存储 

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution(object):def levelOrder(self, root):""":type root: TreeNode:rtype: List[int]"""if root is None:return []quene = [root]res = []while quene:node = quene.pop(0)res.append(node.val)if node.left is not None:quene.append(node.left)if node.right is not None:quene.append(node.right)return res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:vector<int> levelOrder(TreeNode* root) {vector<int>res;if(!root){return {};}queue<TreeNode*> queue_A;queue_A.push(root);while(!queue_A.empty()){TreeNode* node = queue_A.front();res.push_back(node->val);queue_A.pop();if(node->left){queue_A.push(node->left);}if(node->right){queue_A.push(node->right);}}return res;}
};

1-7.从上到下打印二叉树 II

思路：从跟节点开始一层一层遍历

1.递归法：要注意的是判断节点是同一层，此时可以传入一个level参数用于控制层数

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def levelOrder(self, root: TreeNode) -> List[List[int]]:res = []def backtrace(t, level):if t:if len(res)==level:res.append([])res[level].append(t.val)backtrace(t.left,level+1)backtrace(t.right,level+1)backtrace(root,0)return res

2.迭代法 BFS

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def levelOrder(self, root: TreeNode) -> List[List[int]]:res = []if not root:return resquene= [root]while quene:            temp = []# print('==len(quene):', len(quene))for i in range(len(quene)):node = quene.pop(0)temp.append(node.val)  # print('==temp:', temp)                if node.left:quene.append(node.left)if node.right:          quene.append(node.right)res.append(temp)return res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> res;        if(!root){return {};}queue<TreeNode* > queue_A;queue_A.push(root);while(!queue_A.empty()){ vector<int> temp_res;int count = queue_A.size();for (int i=0;i<count;i++){                TreeNode* node = queue_A.front();temp_res.push_back(node->val);queue_A.pop();if(node->left){queue_A.push(node->left);}if(node->right){queue_A.push(node->right);}}res.push_back(temp_res);            }return res;}};

1-8.从上到下打印二叉树 III

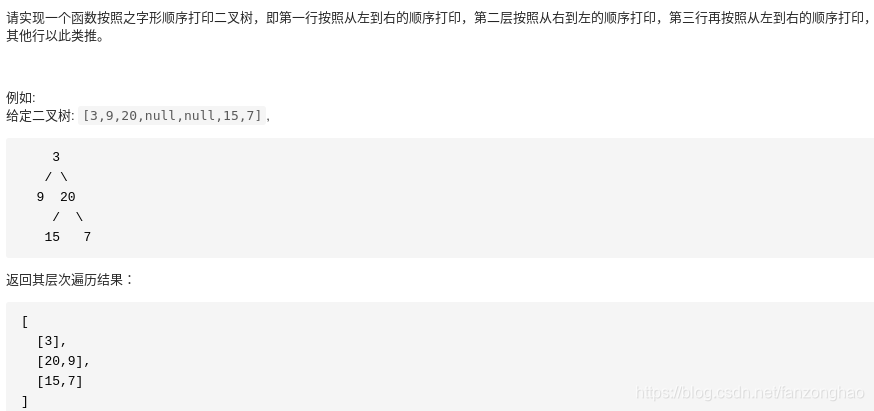
1.思路BFS :将每一层节点存入队列进行遍历,对奇数层进行逆序加入即可

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution(object):def levelOrder(self, root):""":type root: TreeNode:rtype: List[List[int]]"""if root is None:return []quene = [root]res =[]while quene:temp = []for i in range(len(quene)):node = quene.pop(0)temp.append(node.val)if node.left is not None:quene.append(node.left)                if node.right is not None:quene.append(node.right)if len(res)%2==1:res.append(temp[::-1])else:res.append(temp)# print('==res:', res)return res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector <int>> res;if (root==NULL){return {};}queue<TreeNode* > queue_A;queue_A.push(root);while(!queue_A.empty()){vector <int> temp_res;int count = queue_A.size();for (int i=0;i<count;i++){TreeNode* node =  queue_A.front();                temp_res.push_back(node->val);queue_A.pop();if(node->left){queue_A.push(node->left);}if(node->right){queue_A.push(node->right);}}if(res.size()%2==0){res.push_back(temp_res);}else{reverse(temp_res.begin(),temp_res.end());res.push_back(temp_res);}            }return res;}
};

 1-9.二叉树的锯齿形层次遍历

思路:将每一层的结果进行保存,最后在奇数层反转即可

1.递归解法 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def help(self,node,level):if node:if len(self.res) == level:self.res.append([])self.res[level].append(node.val)self.help(node.left,level+1)self.help(node.right,level+1)def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:self.res = []if root is None:return self.resself.help(root, 0)for i in range(len(self.res)):if i%2==1:self.res[i] = self.res[i][::-1]return self.res

2.迭代解法


# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:res = []if root is None:return resquene = [root]while quene:temp = []for i in range(len(quene)):node = quene.pop(0)temp.append(node.val)if node.left is not None:quene.append(node.left)if node.right is not None:quene.append(node.right)res.append(temp)for i in range(len(res)):if i%2==1:res[i] = res[i][::-1]        return res

1-10.递增顺序查找树

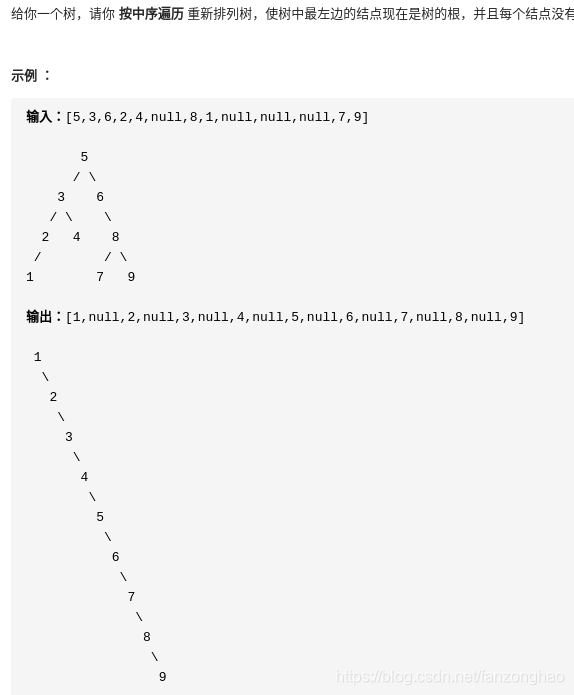
思路:中序遍历获取每个节点的值,在利用值构建树 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def increasingBST(self, root: TreeNode) -> TreeNode:res= []if root is None:return resdef helper(node):if node:helper(node.left)res.append(node.val)helper(node.right)helper(root)print('res:', res)#构建树new_node = TreeNode(res[0])current_node=new_nodefor i in range(len(res)-1):current_node.left = Nonecurrent_node.right = TreeNode(res[i+1])current_node = current_node.rightreturn new_node

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector <int> res;void help(TreeNode* node){if(node == nullptr){return ;}help(node->left);res.push_back(node->val);help(node->right);}TreeNode* increasingBST(TreeNode* root) {if(root == nullptr){return nullptr;}help(root);TreeNode* new_root = new TreeNode(res[0]);TreeNode* temp_node = new_root;for(int i=1;i<res.size();i++){temp_node->left = nullptr;temp_node->right = new TreeNode(res[i]);temp_node = temp_node->right;}return new_root;}
};

 1-11. 二叉树的右视图

思路：每一层进行遍历存储结果,将每一层的右侧结果进行输出即可。

1.迭代法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def rightSideView(self, root: TreeNode) -> List[int]:res = []if root is None:return resqueue = [root]while queue:size = len(queue)for i in range(len(queue)):node = queue.pop(0)if i == size - 1 :res.append(node.val)if node.left is not None:queue.append(node.left)if node.right is not None:queue.append(node.right)return res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int> res;vector<int> rightSideView(TreeNode* root) {if(root == nullptr) {return {};}queue<TreeNode*> queue_A(r);queue_A.push(root);while(!queue_A.empty()){int count = queue_A.size();for (int i = 0; i < count; i++){TreeNode* temp_node = queue_A.front();if(i == count - 1){res.push_back(temp_node->val);}queue_A.pop();if(temp_node->left!=nullptr){queue_A.push(temp_node->left);}if(temp_node->right!=nullptr){queue_A.push(temp_node->right);}                }}return res;}
};

2.递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def rightSideView(self, root: TreeNode) -> List[int]:res =[]if root is None:return resdef helper(node, level):if node is not None:if len(res) == level:res.append([])res[level].append(node.val)helper(node.left,level+1)helper(node.right,level+1)helper(root, 0)# print('====res:', res)fin_res =[]for i in range(len(res)):fin_res.append(res[i][-1])return fin_res

1-12. 找树左下角的值

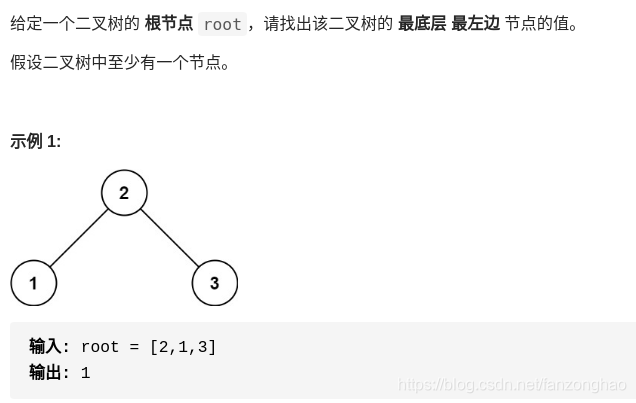
思路:bfs

python:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def findBottomLeftValue(self, root: TreeNode) -> int:nodes = [root]res = []while nodes:temp = nodes[0]for i in range(len(nodes)):node = nodes.pop(0)if node.left:nodes.append(node.left)if node.right:nodes.append(node.right)    if len(nodes) == 0:return temp.val

c++:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int findBottomLeftValue(TreeNode* root) {queue<TreeNode* > nodes;nodes.push(root);while(!nodes.empty()){TreeNode* temp = nodes.front();int count = nodes.size();for(int i = 0; i < count; i++){TreeNode* node = nodes.front();nodes.pop();if(node->left){nodes.push(node->left);}if(node->right){nodes.push(node->right);}}if(nodes.size() == 0){return temp->val;}}return -1;}
};

2-1.二叉树的深度

递归:python代码

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution(object):def maxDepth(self, root):""":type root: TreeNode:rtype: int"""if not root:return 0return max(self.maxDepth(root.left),self.maxDepth(root.right))+1

c++代码:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int maxDepth(TreeNode* root) {if(root==NULL){return 0;}return max(maxDepth(root->left),maxDepth(root->right))+1;}
};

2-2：二叉树的最小深度

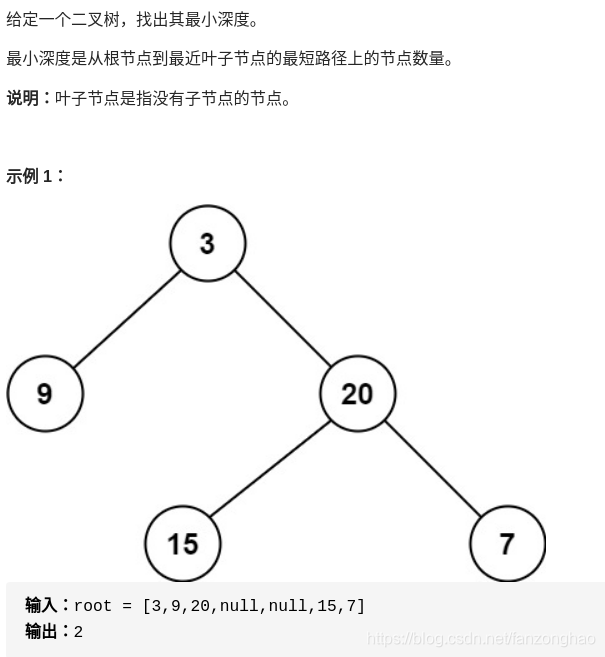
思路;求的就是根节点到叶子节点的最小值

python代码:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def minDepth(self, root: TreeNode) -> int:if root is None:return 0if root.left and root.right:return min(self.minDepth(root.left),self.minDepth(root.right))+1elif root.left:return self.minDepth(root.left)+1else:return self.minDepth(root.right)+1

 c++代码:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {if (root == nullptr){return 0;}if(root->left && root->right){return min(minDepth(root->left),minDepth(root->right))+1;}else if(root->left){return minDepth(root->left)+1;}else{return minDepth(root->right)+1;}}
};

2-3.二叉树的直径

思路:递归函数用来获取每一层深度，然后在分别对左右子树深度求和，这里要注意的是最长直径不一定过根节点，所有要用一个变量存储遍历每个节点时的最大直径．

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def get_depth(self, node):if node is None:return 0l = self.get_depth(node.left)r = self.get_depth(node.right)self.max_value = max(self.max_value, l+r)return max(l,r)+1def diameterOfBinaryTree(self, root: TreeNode) -> int:self.max_value = 0if root is None:return 0self.get_depth(root)return self.max_value

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int max_value=0;int help(TreeNode* node){if(!node){return 0;}int l = help(node->left);int r = help(node->right);max_value =  max(max_value, l+r);return max(l,r)+1;}int diameterOfBinaryTree(TreeNode* root) {help(root);return max_value;}
};

2-4.二叉树中的最大路径和

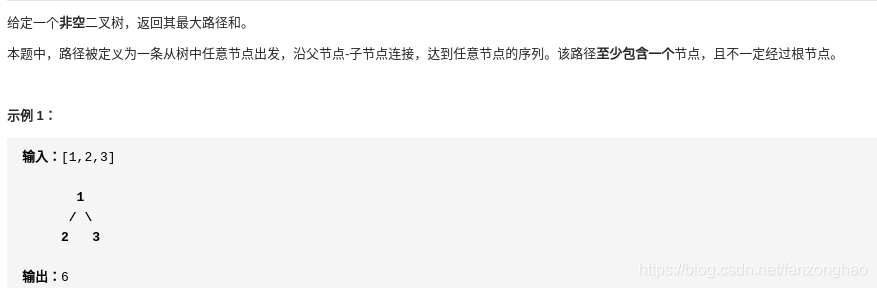
递归　主要是要找准递归终止条件和递归出口,终止条件就是节点为none自然返回值为0, 递归出口就是节点本身值+max(左节点增益值，右节点增益值)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def helper(self, node):if node is None:return 0left_gain = self.helper(node.left)right_gain = self.helper(node.right)self.max_gain = max(self.max_gain,left_gain+right_gain+node.val)return max(node.val+left_gain,node.val+right_gain,0)def maxPathSum(self, root: TreeNode) -> int:self.max_gain = float('-inf')self.helper(root)return self.max_gain

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int max_value=INT_MIN;int helper(TreeNode *node){if(!node){return 0;}int left_gain = helper(node->left);int right_gain = helper(node->right);max_value = max(max_value, node->val+left_gain+right_gain);return max(max(node->val+left_gain,0),node->val+right_gain);}int maxPathSum(TreeNode* root) {helper(root);return max_value;}
};

2-5.路径总和

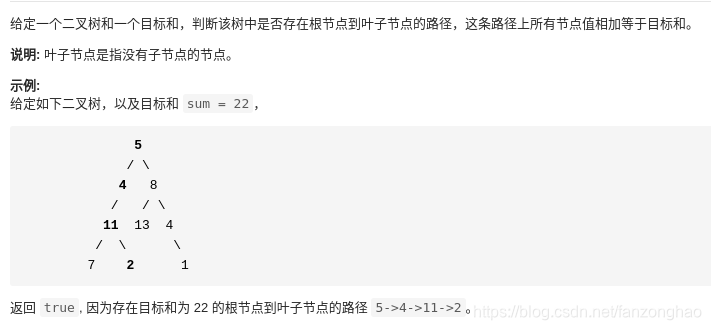
1.递归法 

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution(object):def hasPathSum(self, root, sum):""":type root: TreeNode:type sum: int:rtype: bool"""if not root:return Falseif not root.left and not root.right and root.val==sum:return Truesum -=root.valreturn self.hasPathSum(root.left,sum) or self.hasPathSum(root.right,sum)

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool hasPathSum(TreeNode* root, int targetSum) {if(root == nullptr){return false;}if (root->left == nullptr && root->right == nullptr && targetSum==root->val){return true;}targetSum -=root->val;return hasPathSum(root->left,targetSum) || hasPathSum(root->right,targetSum);}
};

2.利用栈--DFS

class Solution(object):def hasPathSum(self, root, sum):""":type root: TreeNode:type sum: int:rtype: bool"""# # #递归终止条件 # if root is None:#     return False# if root.left is None and root.right is None and root.val == sum:#     return True# sum = sum - root.val# # print('===sum:', sum)# return self.hasPathSum(root.left, sum) or self.hasPathSum(root.right, sum) if not root:return Falsequene = [(root, root.val)]while quene:node,value = quene.pop()if node.left is None and node.right is None and value==sum:return Trueif node.left is not None:quene.append((node.left,value+node.left.val))if node.right is not None:quene.append((node.right,value+node.right.val))   # print('==quene:',quene)return False

3.利用队列--BFS

class Solution(object):def hasPathSum(self, root, sum):""":type root: TreeNode:type sum: int:rtype: bool"""# # #递归终止条件 # if root is None:#     return False# if root.left is None and root.right is None and root.val == sum:#     return True# sum = sum - root.val# # print('===sum:', sum)# return self.hasPathSum(root.left, sum) or self.hasPathSum(root.right, sum) if not root:return Falsequene = [(root, root.val)]while quene:node,value = quene.pop(0)if node.left is None and node.right is None and value==sum:return Trueif node.left is not None:quene.append((node.left,value+node.left.val))if node.right is not None:quene.append((node.right,value+node.right.val))   # print('==quene:',quene)return False

2-6:路径总和 II

思路：回溯　这种里面要调用两层回溯的　　track就不要放在递归函数里面了

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def dfs(self, node, sum_):if node is None:return 0store = self.track.copy()self.track.append(node.val)# print('==self.track:', self.track)if node.left is None and node.right is None and sum_==node.val:         self.res.append(self.track)sum_ -= node.valself.dfs(node.left, sum_)self.dfs(node.right, sum_)# self.track.pop()self.track = storedef pathSum(self, root: TreeNode, sum: int) -> List[List[int]]:self.res = []self.track = []self.dfs(root, sum)return self.res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> res;vector<int> track;void dfs(TreeNode* root, int targetSum){if(root==nullptr){return ;}vector<int> store;store = track;track.push_back(root->val);        if(root->left==nullptr && root->right==nullptr && targetSum==root->val){res.push_back(track);}targetSum -= root->val;dfs(root->left, targetSum);dfs(root->right, targetSum);track = store;}vector<vector<int>> pathSum(TreeNode* root, int targetSum) {dfs(root, targetSum);return res;}
};

2-7:路径总和 III

思路：用一个列表存储从节点开始的数字和

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
#用列表记录从每一个节点开始的和
class Solution:def dfs(self, node, sum_list, sum):if node is None:return 0 sum_list = [num+node.val for num in sum_list]sum_list.append(node.val)for num in sum_list:if num==sum:self.res+=1self.dfs(node.left, sum_list, sum)self.dfs(node.right, sum_list, sum)def pathSum(self, root: TreeNode, sum: int) -> int:self.res = 0self.dfs(root, [], sum)return self.res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res;void dfs(TreeNode* node, vector<int> num_list, int sum){if(node == nullptr){return ;}for (int i=0; i<num_list.size(); i++){num_list[i] += node->val;}   num_list.push_back(node->val);for(int i=0; i<num_list.size(); i++){if(num_list[i]==sum){res++;}}dfs(node->left, num_list, sum);dfs(node->right, num_list, sum);}int pathSum(TreeNode* root, int sum) {vector<int> num_list;dfs(root, num_list, sum);return res;}
};

2-8.二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径

思路：dfs

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def dfs(self, node,path):if not node:returnpath +=str(node.val)if node.left is None and node.right is None:self.res.append(path)else:path+="->"self.dfs(node.left, path)self.dfs(node.right, path)def binaryTreePaths(self, root: TreeNode) -> List[str]:self.res = []self.dfs(root, "")return self.res

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> res;void dfs(TreeNode* node, string path){if(node == nullptr){return ;}path+=to_string(node->val);if(node->left == nullptr && node->right == nullptr){res.push_back(path);}else{path+="->";dfs(node->left, path);dfs(node->right, path);}}vector<string> binaryTreePaths(TreeNode* root) {dfs(root, "");return res;}
};

2-9.求根节点到叶节点数字之和

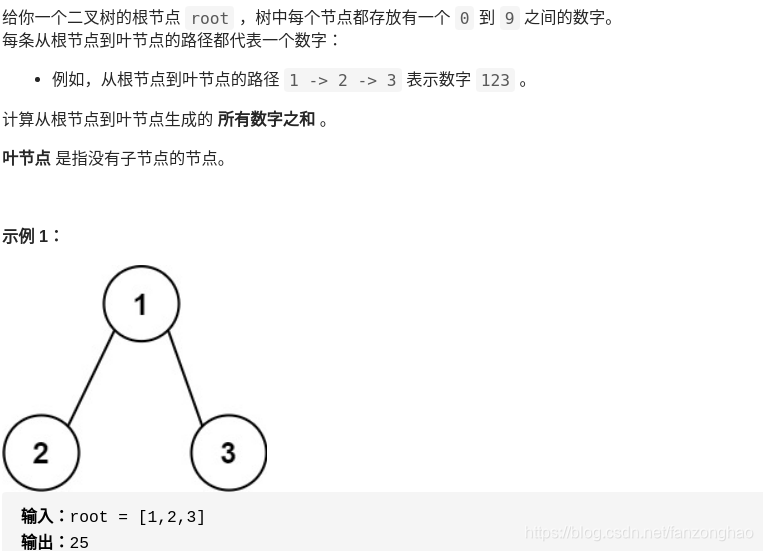
python:

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def help(self, node, path):if node is None:returnpath += str(node.val)if node.left is None and node.right is None:self.res.append(path)else:            self.help(node.left, path)self.help(node.right, path)def sumNumbers(self, root: TreeNode) -> int:self.res = []self.help(root, '')return sum(map(int, self.res))

ｃ++代码:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<string> res;void help(TreeNode* node, string path){if(node == nullptr){return ;}path += to_string(node->val);if(node->left == nullptr && node->right == nullptr){res.push_back(path);}else{help(node->left, path);help(node->right, path);}}int sumNumbers(TreeNode* root) {help(root, "");int int_res;for(auto str_:res){int_res += atoi(str_.c_str());}return int_res;}
};

3-1.合并二叉树

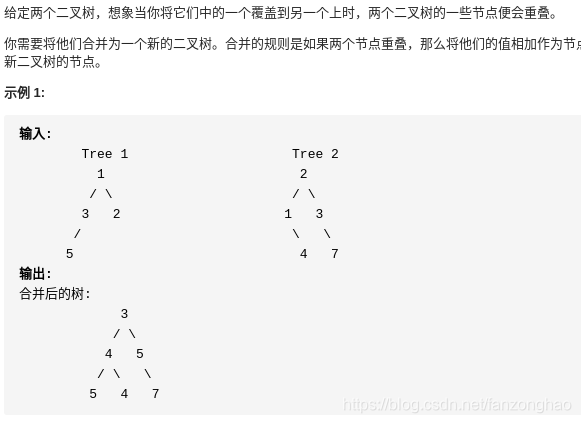
思路:采用前序遍历访问二叉树，如果节点其一为none，就返回另一个

1.递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:if t1 is None:return t2if t2 is None:return t1t1.val+=t2.valt1.left = self.mergeTrees(t1.left,t2.left)t1.right = self.mergeTrees(t1.right,t2.right)return t1

2.迭代法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def mergeTrees(self, t1: TreeNode, t2: TreeNode) -> TreeNode:if t1 is None:return t2stack= [(t1,t2)]while stack:t = stack.pop()if t[0] is None or t[1] is None:continuet[0].val +=t[1].valif t[0].left is None:t[0].left = t[1].leftelse:stack.append((t[0].left, t[1].left))if t[0].right is None:t[0].right = t[1].rightelse:stack.append((t[0].right, t[1].right))return t1

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {if(root1 == nullptr){return root2;}if(root2 == nullptr){return root1;}root1->val += root2->val;root1->left = mergeTrees(root1->left, root2->left);root1->right = mergeTrees(root1->right, root2->right);return root1;}
};

3-2：翻转二叉树

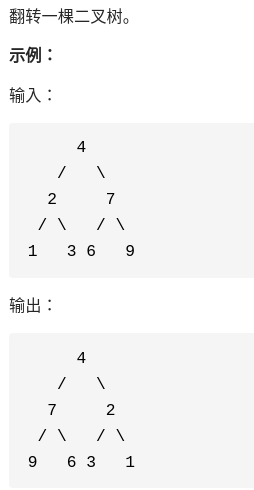
思路:递归遍历左右子树进行交换即可

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def invertTree(self, root: TreeNode) -> TreeNode:if root is None:return Noneleft = self.invertTree(root.left)right = self.invertTree(root.right)root.left = rightroot.right = leftreturn root

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* invertTree(TreeNode* root) {if(root == nullptr){return nullptr;}TreeNode* left = invertTree(root->left);TreeNode* right = invertTree(root->right);root->left = right;root->right = left;return root;}
};

3-3.检查二叉树平衡性

思路：递归求解节点左右分支的最长路径，如果路径之差绝对值大于1，就认为是非平衡。 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def depth(self, node):if node is None:return 0return max(self.depth(node.left), self.depth(node.right)) + 1def isBalanced(self, root: TreeNode) -> bool:if root is None:return Trueif abs(self.depth(root.left) - self.depth(root.right)) > 1:return Falsereturn self.isBalanced(root.left) and self.isBalanced(root.right)

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int get_height(TreeNode* node){if(node == NULL){return 0;}return max(get_height(node->left), get_height(node->right))+1;}bool isBalanced(TreeNode* root) {if(root == NULL){return true;}int left_value = get_height(root->left);int right_value = get_height(root->right);// cout<<left_value<<endl;// cout<<right_value<<endl;if(abs(left_value-right_value)>1){return false;}return isBalanced(root->left) && isBalanced(root->right);}
};

3-4.对称二叉树

1.解法1 bfs 对每个节点的左子树和右子树进行判断相等

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def isSymmetric(self, root: TreeNode) -> bool:def check(t1,t2):if t1==None and t2==None:return Trueif t1==None or t2==None:return Falseif (t1.val != t2.val):return Falsereturn check(t1.left,t2.right) and check(t1.right,t2.left)return check(root,root)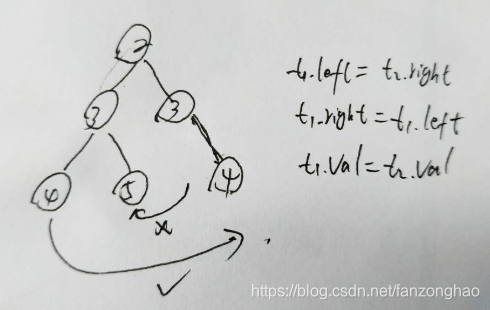

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool dfs(TreeNode* t1, TreeNode* t2){if(t1==nullptr && t2==nullptr){return true;}if(t1==nullptr || t2==nullptr){return false;}return dfs(t1->left,t2->right) && dfs(t1->right,t2->left);}bool isSymmetric(TreeNode* root) {return dfs(root, root);}
};

2.解法2 dfs ，首先对根节点左子树进行前序遍历并存储值，对根节点右子树的右分支进行遍历在对左分支进行遍历并存储值，最后比较两个列表的值。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def isSymmetric(self, root: TreeNode) -> bool:if root==None:return Truedef leftsearch(t1, left):if t1==None:left.append(None)else:left.append(t1.val)leftsearch(t1.left,left)leftsearch(t1.right,left)def rightsearch(t2, right):if t2==None:right.append(None)else:right.append(t2.val)rightsearch(t2.right,right)rightsearch(t2.left,right)left = []right = []leftsearch(root.left, left)rightsearch(root.right, right)if left==right:return Trueelse:return False

3-5.相同的树

思路：判断节点 相等 判断节点的值相等 在递归左右子树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:if not p and not q:#两个节点都为空return Trueif (not p and q) or (not q and p):#两个节点只要有一个不为空return Falseif p.val != q.val:return Falsereturn self.isSameTree(p.left,q.left) and self.isSameTree(p.right,q.right)

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool isSameTree(TreeNode* p, TreeNode* q) {if(p==nullptr && q==nullptr){return true;}if(p==nullptr || q==nullptr){return false;}if(p->val != q->val){return false;}return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);}
};

3-6.左叶子之和

思路：判断左叶子的条件：节点的左指针不为none,同时节点的左指针的左指针和节点的左指针的右指针为none

1.递归写法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def sumOfLeftLeaves(self, root: TreeNode) -> int:self.result = 0  def get_res(t):if t is None:return 0 if t is not None and t.left is not None and t.left.left is None and t.left.right is None:self.result = self.result + t.left.val    get_res(t.left)get_res(t.right)get_res(root)return self.result

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:int res;void help(TreeNode* node){if(node == NULL){return ;}if(node->left !=NULL && node->left->left ==NULL && node->left->right ==NULL){res+=node->left->val;}help(node->left);help(node->right);}int sumOfLeftLeaves(TreeNode* root) {if(root == NULL){return 0;}help(root);return res;}
};

2.迭代写法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def sumOfLeftLeaves(self, root: TreeNode) -> int:if root is None:return 0 stack = [root]res = 0while stack:node = stack.pop()if node is not None:if node.left is not None and node.left.left is None and node.left.right is None:res += node.left.valstack.append(node.left)stack.append(node.right)return res

4-1.从前序与中序遍历序列构造二叉树

思路：

终止条件:前序或中序数组为空．
根据前序数组第一个元素，拼出根节点，再将前序数组和中序数组分成两半，递归的处理前序数组左边和中序数组左边，递归的处理前序数组右边和中序数组右边。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:        # 递归终止条件 前序遍历节点数或中序遍历节点数为０if len(preorder)==0 or len(inorder)==0:return Noneroot = TreeNode(preorder[0])#根据前序遍历特点创建根节点#再根据中序遍历特点用根节点找出左右子树的分界点mid_index = inorder.index(preorder[0])#再利用中序遍历和前序遍历的左子树节点个数相等特点　构造根节点左子树root.left = self.buildTree(preorder[1:mid_index+1],inorder[:mid_index])#再利用中序遍历和前序遍历的右子树节点个数相等特点　构造根节点右子树root.right = self.buildTree(preorder[mid_index+1:],inorder[mid_index+1:])return root

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.empty() || preorder.empty()) {return nullptr;}TreeNode* root = new TreeNode(preorder[0]);int root_value = preorder[0];int middle = 0;for (int i=0;i<inorder.size();i++){if(inorder[i]==root_value){middle = i;break;}}vector<int> leftInorder(inorder.begin(), inorder.begin() + middle);vector<int> rightInorder(inorder.begin() + middle + 1, inorder.end());vector<int> leftPreorder(preorder.begin()+1, preorder.begin() + middle+1);vector<int> rightPreorder(preorder.begin() + middle + 1, preorder.end());root->left = buildTree(leftPreorder,leftInorder);root->right = buildTree(rightPreorder,rightInorder);return root;}
};

4-2.从中序与后序遍历序列构造二叉树

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if(inorder.empty() || postorder.empty()){return nullptr;}TreeNode* root = new TreeNode(postorder[postorder.size()-1]);int root_value = postorder[postorder.size()-1];int middle = 0;for (int i=0; i<inorder.size(); i++){if(inorder[i] == root_value){middle = i;break;}}// cout<<"===middle:"<<middle<<endl;vector<int> left_inorder(inorder.begin(), inorder.begin() + middle);vector<int> right_inorder(inorder.begin() + middle + 1, inorder.end());vector<int> left_postorder(postorder.begin(), postorder.begin() + middle);vector<int> right_postorder(postorder.begin() + middle, postorder.end() - 1);root->left = buildTree(left_inorder, left_postorder);root->right = buildTree(right_inorder, right_postorder);return root;}
};

 思路：和上一题类似

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:#递归终止条件if len(inorder)==0 or len(postorder)==0:return None#创建根节点root = TreeNode(postorder[-1])#根据中序遍历获取分离点mid_index = inorder.index(postorder[-1])# print('==mid_index:',mid_index)#获取左子树root.left = self.buildTree(inorder[:mid_index],postorder[:mid_index])#获取右子树root.right = self.buildTree(inorder[mid_index+1:],postorder[mid_index:-1])return root

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if(inorder.empty() || postorder.empty()){return nullptr;}TreeNode* root = new TreeNode(postorder[postorder.size()-1]);int root_value = postorder[postorder.size()-1];int middle = 0;for (int i=0; i<inorder.size(); i++){if(inorder[i] == root_value){middle = i;break;}}// cout<<"===middle:"<<middle<<endl;vector<int> left_inorder(inorder.begin(), inorder.begin() + middle);vector<int> right_inorder(inorder.begin() + middle + 1, inorder.end());vector<int> left_postorder(postorder.begin(), postorder.begin() + middle);vector<int> right_postorder(postorder.begin() + middle, postorder.end() - 1);root->left = buildTree(left_inorder, left_postorder);root->right = buildTree(right_inorder, right_postorder);return root;}
};

由上面两题可知对于前序遍历：跟左右，中序遍历：左跟右，后序遍历左右跟；

采前序遍历和中序遍历，中序遍历和后序遍历都能通过根节点分离出左右，而前序遍历和后序遍历就不能，故而后者无法恢复出二叉树．

4-3.二叉树的序列化与反序列化

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Codec:def serialize(self, root):"""Encodes a tree to a single string.:type root: TreeNode:rtype: str"""# return self.pre_order(root)# self.in_order(root)from collections import dequeres = []queue= [root]#deque([root])while queue:root = queue.pop(0)#left()if root:res.append(root.val)queue.extend([root.left, root.right])else:res.append('#')return str(res)def deserialize(self, data):"""Decodes your encoded data to tree.:type data: str:rtype: TreeNode"""# print(self.pre_rest, self.in_res)print(data)nodes = [(TreeNode(v) if v != '#' else None) for v in eval(data)]i, j, n = 0, 1, len(nodes)while j < n:if nodes[i]:nodes[i].left = nodes[j]j += 1nodes[i].right = nodes[j]j += 1i += 1return nodes[0]    # Your Codec object will be instantiated and called as such:
# ser = Codec()
# deser = Codec()
# ans = deser.deserialize(ser.serialize(root))

5-1.二叉搜索树的最近公共祖先

思路：

1.从根节点开始遍历树
2.如果节点 p 和节点 q 都在右子树上，那么以右孩子为根节点继续 1 的操作
3.如果节点 p 和节点 q 都在左子树上，那么以左孩子为根节点继续 1 的操作
4.如果条件 2 和条件 3 都不成立，这就意味着我们已经找到p 和q 的公共祖先了

解法1:当成普通二叉树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':if root==p or root==q or root is None:return rootleft_node = self.lowestCommonAncestor(root.left,p,q)right_node = self.lowestCommonAncestor(root.right,p,q)if left_node is None:return right_nodeif right_node is None:return left_nodereturn root

解法2利用二叉搜索树特点根节点值和左右子树值大小的特点.递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#利用二叉搜索树的特点
class Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':print('==root.val:', root.val)if root.val< min(p.val, q.val):#都大于根节点的值 将右孩子作为根节点return self.lowestCommonAncestor(root.right, p, q)elif root.val > max(p.val, q.val):#都小于根节点的值 将左孩子作为根节点return self.lowestCommonAncestor(root.left, p, q)else:#找到公共祖先return root

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if(root->val<min(p->val,q->val)){return lowestCommonAncestor(root->right,p,q);}if(root->val>max(p->val,q->val)){return lowestCommonAncestor(root->left,p,q);}return root;}
};

解法3.迭代法

#利用二叉搜索树的特点
class Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':node = rootwhile node:if node.val < min(p.val,q.val):node = node.rightelif node.val > max(p.val,q.val):node = node.leftelse:return node

5-2:二叉树的最近公共祖先

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':if root is None or root==p or root==q:#递归终止条件　节点为空　或者节点等于p,q其中之一return rootleft = self.lowestCommonAncestor(root.left, p, q)#遍历左子树right = self.lowestCommonAncestor(root.right, p, q)#遍历右子树if left is None:#左子树为空　就去右子树　return rightif right is None:#右子树为空　就去左子树　return leftreturn root#左右子树都不为空　说明找到了节点　

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {if (root == NULL){return NULL;}if(root->val == p->val || root->val == q->val){return root;}TreeNode* left_node = lowestCommonAncestor(root->left,p,q);TreeNode* right_node = lowestCommonAncestor(root->right,p,q);if(left_node !=NULL && right_node!=NULL){return root;}if (left_node==NULL){return right_node;}return left_node;}
};

5-3.二叉搜索树中的搜索

思路：利用二叉树特点

1.从根节点遍历二叉树

2.如果给定值小于跟节点值，根节点替换为右孩子节点，否则根节点替换为左孩子节点

1.递归法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#递归法
class Solution:def searchBST(self, root: TreeNode, val: int) -> TreeNode:if not root or root.val ==val:#截止条件return rootif root.val < val:return self.searchBST(root.right,val)else:return self.searchBST(root.left,val)

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if(root == nullptr){return root;}if(root->val == val){return root;}if(root->val > val){return searchBST(root->left,val);}else{return searchBST(root->right,val);}}
};

2.迭代法

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
#迭代法
class Solution:def searchBST(self, root: TreeNode, val: int) -> TreeNode:while root is not None and root.val !=val:root = root.left if root.val >val else root.rightreturn root

5-4.把二叉搜索树转换为累加树 

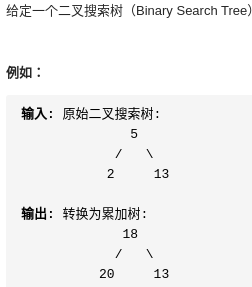
思路：其实就是逆中序遍历，利用二叉搜索树的特点，跟节点值更新为右孩子和根节点值之和，左孩子值更新为根节点与左孩子值之和。

1.迭代法：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def convertBST(self, root: TreeNode) -> TreeNode:stack = []node = rootvalue = 0while stack or node:while node:#把跟节点与右子树节点依次压进栈 实现逆中序遍历stack.append(node)node = node.rightprint('==stack:', stack)node = stack.pop()print('==node:',node)value += node.valnode.val = valueprint('==node.left:', node.left)node = node.leftreturn root

2.递归法：

其中res存储逆中序遍历(右根左)的值，便于查看

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def helper(self, node):if node:self.helper(node.right)# self.res.append(node.val)self.value+=node.valnode.val = self.valueself.helper(node.left)def convertBST(self, root: TreeNode) -> TreeNode:# self.res =[]self.value = 0self.helper(root)return root

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int res = 0;void help(TreeNode* node){if(node == nullptr){return ;}help(node->right);res += node->val;node->val = res;help(node->left);}TreeNode* convertBST(TreeNode* root) {help(root);return root;}
};

5-5.删除二叉搜索树中的节点

#思路：中序遍历，如果值大于节点值，则去右子树，否则去左子树
#如果 找的的节点是叶子节点，则进行删除置None即可
#如果找到的节点不是叶子节点，有右子树，则用后继节点(比当前节点值大的最小值)代替找到的节点，在将后继节点置None
#如果找到的节点不是叶子节点，有左子树，则用前驱节点(比当前节点值小的最大值)代替找到的节点，在将前驱节点置None 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:#获取节点的后继节点(比当前节点大的最小值)def get_successor(self, node):node = node.rightwhile node.left:node = node.leftreturn node.val#获取节点的前驱节点(比当前节点小的最大值)def get_pressor(self, node):node = node.leftwhile node.right:node = node.rightreturn node.valdef deleteNode(self, root: TreeNode, key: int) -> TreeNode:if root is None:return Noneif root.val<key:root.right = self.deleteNode(root.right, key)elif root.val>key:root.left = self.deleteNode(root.left, key)else:if root.left is None and root.right is None:#叶子节点root = None                elif root.right:#要删除的节点有右子树 利用后继节点root.val = self.get_successor(root)root.right = self.deleteNode(root.right,root.val)#删除后继节点else:#要删除的节点有左子树 利用前驱节点root.val = self.get_pressor(root)root.left = self.deleteNode(root.left,root.val)#删除前驱节点                    return root

c++实现: 

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int get_succesor(TreeNode* node){//得到后继节点node = node->right;while(node->left != nullptr){node = node->left;}return node->val;}int get_pressor(TreeNode* node){node = node->left;while(node->right != nullptr){node = node->right;}return node->val;}TreeNode* deleteNode(TreeNode* root, int key) {if(root == nullptr){return nullptr;}if(root->val < key){root->right= deleteNode(root->right, key);}else if(root->val >key){root->left= deleteNode(root->left, key);}else{if(root->left == nullptr && root->right == nullptr){root = nullptr;}else if(root->right != nullptr){root->val = get_succesor(root);root->right = deleteNode(root->right, root->val);}else{root->val = get_pressor(root);root->left = deleteNode(root->left, root->val);}}return root;}
};

5-6.不同的二叉搜索树

思路:卡塔兰数

将 1⋯(i−1) 序列作为左子树，将 (i+1)⋯n 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。

在上述构建的过程中，由于根的值不同，因此我们能保证每棵二叉搜索树是唯一的.也就得到卡塔兰数

class Solution(object):def numTrees(self, n):""":type n: int:rtype: int"""#状态方程 和G(j-1) * G(n-j)dp = [0]*(n+1)#0 1树都为1dp[0], dp[1] = 1, 1for i in range(2,n+1):for j in range(1,i+1):dp[i] += dp[j-1]*dp[i-j]# print('==dp:', dp)return dp[-1]

c++实现:

class Solution {
public:int numTrees(int n) {vector<int> res(n+1,0);    res[0] = 1;res[1] = 1;for (int i=2;i<n+1;i++){for (int j=1;j<i+1;j++){res[i] += res[j-1] * res[i-j];}}return res[n];}   
};

5-7.不同的二叉搜索树 II

思路:

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution(object):def generateTrees(self, n):""":type n: int:rtype: List[TreeNode]"""if n==0:return []def build_tree(left,right):if left > right:#递归终止条件 如果左边计数大于右边 说明要返回空值return [None]all_trees = []for i in range(left, right+1):left_trees = build_tree(left, i-1)right_trees = build_tree(i+1, right)for l in left_trees:#遍历可能的左子树for r in right_trees:#遍历可能的右子树cur_tree = TreeNode(i)#根节点cur_tree.left= lcur_tree.right = rall_trees.append(cur_tree)return all_treesres = build_tree(1,n)return res

5.8.验证二叉搜索树

思路1:递归处理右子树节点和 左子树节点的值和上下界限的大小

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution(object):def isValidBST(self, root):""":type root: TreeNode:rtype: bool"""def helper(node, lower=float('-inf'), upper=float('inf')):if node is None:#递归终止条件 节点为Nonereturn Trueval = node.val#获取节点值#如果节点值大于上界或者小于下界 ,返回falseif val >= upper or val <= lower  :return False#递归右子树 对于右子树 具备下界if not helper(node.right, val, upper):return False#递归左子树 对于左子树 具备上界if not helper(node.left, lower, val):return Falsereturn Truereturn helper(root)

c++实现:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool help(TreeNode* node, long long lower,long long upper){if(node == nullptr){return true;}if(node->val <= lower || node->val >= upper){return false;}if(!help(node->right, node->val, upper)){return false;}if(!help(node->left, lower, node->val)){return false;}return true;}bool isValidBST(TreeNode* root) {if(root == nullptr){return true;}return help(root, LONG_MIN, LONG_MAX);}
};

思路2 :利用中序遍历的特点,遍历左子树和根节点,如果值不满足二叉搜索数特点就返回false.

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution(object):def isValidBST(self, root):stack = []node = rootinorder_value = float('-inf')while stack or node:#出栈终止条件while node:#进栈stack.append(node)node = node.leftnode = stack.pop()#左节点# 如果中序遍历得到的节点的值小于等于前一个 inorder_value，说明不是二叉搜索树if node.val <=inorder_value:return Falseinorder_value = node.val node=node.rightreturn True

思路3:递归实现中序遍历　左　跟　右　也就是遍历的后一个节点值要大于上一个　否则不满足二叉搜索树特点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
#中序遍历　左跟右
class Solution:def __init__(self):self.pre = float('-inf')def isValidBST(self, root: TreeNode) -> bool:if root is None:return Trueif not self.isValidBST(root.left):#先访问左子树return Falseif root.val<=self.pre:#在访问当前节点return False;print('==before self.pre:',self.pre)self.pre = root.valprint('==after self.pre:',self.pre)return self.isValidBST(root.right)#在访问右子树

5.9将有序数组转换为二叉搜索树

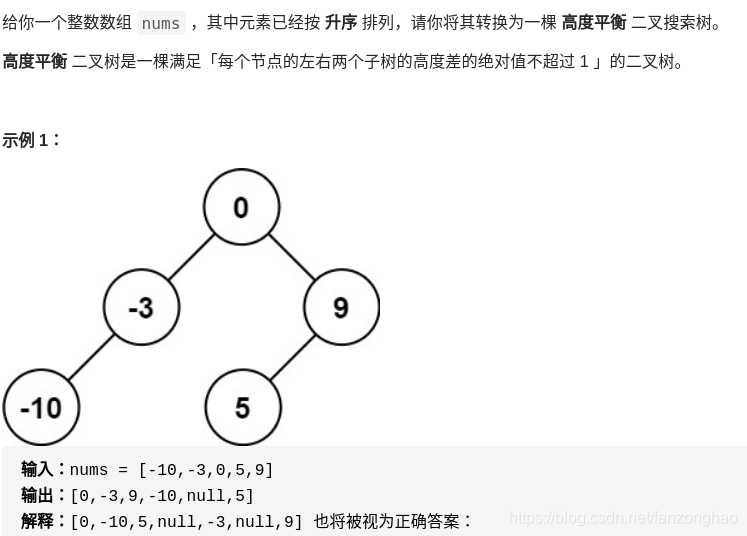
思路:二分法

python代码 

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def help(self, left, right):if left > right:return Nonemid = left + (right - left) // 2root = TreeNode(self.nums[mid])root.left = self.help(left, mid - 1)root.right = self.help(mid + 1, right)return rootdef sortedArrayToBST(self, nums: List[int]) -> TreeNode:    self.nums = numsreturn self.help(0, len(nums) - 1)
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:def help(self, left, right):if left > right:return Nonemid = left + (right - left) // 2root = TreeNode(self.nums[mid])root.left = self.help(left, mid - 1)root.right = self.help(mid + 1, right)return rootdef sortedArrayToBST(self, nums: List[int]) -> TreeNode:    self.nums = numsreturn self.help(0, len(nums) - 1)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/493118.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Eclipse下如何导入jar包

Eclipse下如何导入jar包

原地址&#xff1a;http://blog.csdn.net/justinavril/article/details/2783182 我们在用Eclipse开发程序的时候&#xff0c;经常想要用到第三方的jar包。这时候我们就需要在相应的工程下面导入这个jar包。以下配图说明导入jar包的步骤。 1.右击工程的根目录&#xff0c;点击Pr…
阅读更多...
面对“超人革命”，我们是否已做好准备？

面对“超人革命”，我们是否已做好准备？

来源&#xff1a;资本实验室人类自诞生以来&#xff0c;就一直处在自然规律的支配之下。但自从第一次制造工具并学会使用火的那一刻起&#xff0c;人类就开始走在了持续摆脱大自然生物束缚的道路上。千里听音、力大无穷、不死之身、翱翔天际、深入大洋……各种神话中无需借助外…
阅读更多...
RepVGG

RepVGG

论文链接 一.背景: 现在的一些复杂模型虽然有很高准确度,但是缺点也很明显: 1.多分支,带来了速度的减慢和降低显存的使用率; 2.Mobilenet虽然采用可分离卷积.shufflenet采用分组卷积,带来了flop降低,但是却增加了内存的访问成本(MAC) 二.网络结构 1. 模型 RepVGG在train和…
阅读更多...
2018十大科技丑闻，连娱乐圈都甘拜下风

2018十大科技丑闻，连娱乐圈都甘拜下风

来源&#xff1a;科技日报这一年里&#xff0c;风起云涌的科技界很忙有些人尝到了甜头有些人却吃到了苦头有些事件令人瞠目结舌、难以置信“404”教授梁莹120篇论文凭空蒸发韩春雨论文调查结果被吐槽酸碱体质论与心脏干细胞的创始人双双走下神坛日本福岛核电站污水处理报告错误…
阅读更多...
华为究竟做了多少芯片？

华为究竟做了多少芯片？

来源&#xff1a;半导体行业观察华为依托于旗下的海思大举进军芯片的这个事实已经广为人知了。除了Kirin芯片外&#xff0c;华为在IPC视频编解码和图像信号处理的芯片、电视芯片&#xff0c;Balong基带和NB-IoT芯片等多个领域都取得不错的市场表现&#xff0c;也获得了大家的高…
阅读更多...
leetcode hot100(第一部分) + python(c++)

leetcode hot100(第一部分) + python(c++)

1-1.两数之和 思路&#xff11;&#xff1a;两层for循环　&#xff2f;&#xff08;&#xff4e;2&#xff09; class Solution:def twoSum(self, nums, target):res []for i in range(len(nums)):for j in range(i1, len(nums)):if nums[i]nums[j]target:res.extend([i, j])b…
阅读更多...
云计算深度报告：算力时代迎巨变

云计算深度报告：算力时代迎巨变

来源&#xff1a;中泰证券云计算正进入算力时代供给端:数据存量增长与计算成本下降推动算力需求增长信息技术快速发展与传统产业数据化转型带来大量数据存量。随着云计算、大数据、物联网、人工智能等信息技术的快速发展和传统产业数字化的转型&#xff0c;数据量呈现几何级增长…
阅读更多...
c++将.cpp编译为.so文件

c++将.cpp编译为.so文件

1.首先看文件形式 其中cpp1是直接调用.cpp和生成.so的文件夹。 cpp2是测试生成的.so可以使用的文件夹。 2.先直接编译.cpp检查代码没问题 a.cpp内容: #include <iostream> #include "a.h"void A::readImg(char* path) {B b;b.readImg(path);} a.h内容: …
阅读更多...
vscode debug c++与opencv程序

vscode debug c++与opencv程序

一.工程代码 1.本文调试代码文件夹截图为: 2.代码细节: a.h: #ifndef A_H_ #define A_H_class A {public:A(){}~A(){}void readImg(const char* path);};#endif a.cpp: #include<opencv2/opencv.hpp> #include <iostream> #include "a.h"using name…
阅读更多...
回顾 | 2018年十大AI新闻 中国继续占据主导优势

回顾 | 2018年十大AI新闻 中国继续占据主导优势

来源&#xff1a;网易智能摘要&#xff1a;普华永道&#xff08;PwC&#xff09;估计&#xff0c;到2030年&#xff0c;AI领域的发展将为全球经济贡献15.7万亿美元。本次评选出2018年十大AI新闻&#xff0c;它们囊括各个领域&#xff0c;有好有坏&#xff0c;从AI突破和新投资&…
阅读更多...
新科技快速指南系列之“5G”：历史、现在与未来

新科技快速指南系列之“5G”：历史、现在与未来

来源&#xff1a;36氪摘要&#xff1a;5G仍然让人感觉很遥远。但是这些碎片正在拼凑在一起。未来取决于连通性&#xff08;connectivity&#xff09;。从人工智能和自动驾驶汽车到远程医疗和混合现实&#xff0c;再到迄今为止无法想象的技术&#xff0c;所有我们希望能够让我们…
阅读更多...
torch版ResNet50(带有多输出)转c++ tensorrt

torch版ResNet50(带有多输出)转c++ tensorrt

第一个最简单的lenet示例请参考这篇文章 一.torch阶段 测试图片: torch代码: # coding:utf-8 import torch from torch import nn from torch.nn import functional as F import torchvision import os import struct import time import cv2 import numpy as npdef main()…
阅读更多...
新一轮全球“太空竞赛”正上演 争夺几万亿美元大蛋糕

新一轮全球“太空竞赛”正上演 争夺几万亿美元大蛋糕

来源&#xff1a;华尔街见闻摘要&#xff1a;太空竞赛不可避免受到民族自豪感的刺激和数万亿美元产业的诱惑。到2040年&#xff0c;摩根士丹利估计&#xff0c;太空经济规模将有1.1万亿美元&#xff1b;美国银行估计将达到2.7万亿美元。冷战时期的太空竞赛&#xff0c;又重新降…
阅读更多...
ubuntu16.04编译安装c++ opencv与vscode配置debug

ubuntu16.04编译安装c++ opencv与vscode配置debug

一&#xff0e;编译安装c opencv 1.下载zip包 本文安装的是opencv3.4.3,下载链接&#xff0c;以Sources方式下载zip包&#xff0e; 2.安装依赖 sudo apt-get install build-essential sudo apt-get install cmake git libgtk2.0-dev pkg-config libavcodec-dev libavformat…
阅读更多...
【年终盘点】2018年十大新型机器人

【年终盘点】2018年十大新型机器人

来源&#xff1a;网易智能摘要&#xff1a;2018年&#xff0c;机器人行业迎来了丰收——随着新型机器和高级人工智能的出现&#xff0c;各类机器人都在各自的领域都取得了重大的进步&#xff0c;例如家用机器人、工业机器人、医疗机器人、生物机器人和玩具机器人。今年&#xf…
阅读更多...
leetcode hot100(第二部分) + python(c++)

leetcode hot100(第二部分) + python(c++)

50-1. 乘积最大子数组 思路1:找到状态转移方程: maxf[i]:表示在i处最大连乘数 minf[i]:表示在i处最小连乘数 maxf[i] max(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1]) minf[i] min(nums[i],nums[i]*minf[i-1],nums[i]*maxf[i-1]) #maxf[i]:表示在i处最大连乘数 #minf[i]…
阅读更多...
自动驾驶真的会来得那么快吗：关于自动驾驶的7个疑问

自动驾驶真的会来得那么快吗：关于自动驾驶的7个疑问

来源&#xff1a;资本实验室自动驾驶汽车的研发已经成为全球热潮。无论是像谷歌、百度、Uber这样的互联网巨头&#xff0c;还是丰田、通用、福特这样的老牌汽车制造商&#xff0c;都在以大量的人力、资金向自动驾驶领域下注。然而&#xff0c;无论是Waymo推出首个自动驾驶汽车商…
阅读更多...
git的一些操作

git的一些操作

一.git工作原理/流程: workspace: (除去.git)看见的目录。 版本库(Repository)&#xff1a;工作区有一个隐藏目录.git就叫版本库。其中版本库里面存了很多东西&#xff0c;最重要的就是stage(暂存区)&#xff0c;还有Git为我们自动创建了第一个分支master,以及指向master的一…
阅读更多...
从GE数字化业务大调整看工业互联网未来

从GE数字化业务大调整看工业互联网未来

来源&#xff1a;财经杂志2018年&#xff0c;工业互联网依然是制造业数字化转型中最热的话题&#xff0c;“工业4.0”、“中国制造2025”这些制造业的热门话题在热度上已经明显让位于工业互联网。工信部官网信息显示&#xff0c;从1月国务院发布《关于深化“互联网先进制造业”…
阅读更多...
clion卸载+clion连接docker编写trt程序

clion卸载+clion连接docker编写trt程序

一.卸载 # 删除安装文件夹 1.rm -r clion-2021.1.1 # 删除配置文件 2.sudo rm -rf ~/.config/JetBrains/CLion2021.1 二.连接docker 由于本地机器没有gpu,学习trt加速模型很难受,经过一段时间摸索和请教别人,最后采用clion连接docker进行trt学习,下载安装很简单,这里主要介绍…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023