1-1.两数之和

思路1:两层for循环 O(n2)
class Solution:def twoSum(self, nums, target):res = []for i in range(len(nums)):for j in range(i+1, len(nums)):if nums[i]+nums[j]==target:res.extend([i, j])breakprint('==res:', res)return res
nums = [2, 7, 6, 15]
target = 9
sol = Solution()
sol.twoSum(nums, target)![]()
思路2:hash
python代码
class Solution:def twoSum(self, nums, target):res_dict = {}for i in range(len(nums)):value = target - nums[i]if value in res_dict:return [res_dict[value], i]res_dict[nums[i]] = iprint('==res_dict:', res_dict)return [-1, -1]nums = [2, 7, 6, 15]
target = 9
sol = Solution()
res = sol.twoSum(nums, target)
print('res:', res)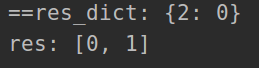
思路2:c++代码:
#include <string>
#include <iostream>
#include <vector>
#include <list>
#include <map>
#include <typeinfo>using namespace std;class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {map<int, int> dict_;for(int k=0;k<nums.size();k++){dict_[nums[k]] = k;}map <int,int>::iterator iter = dict_.begin();for (;iter!=dict_.end();iter++){if(dict_[target - iter->first]){// cout<<iter->second<<dict_[target - iter->first]<<endl;return {iter->first,target - iter->first};}}return {-1,-1};}
};int main()
{ vector<int> nums;nums = {2,7,11,15};int target = 9;// nums = [2,7,11,15]Solution sol;vector<int> res;res = sol.twoSum(nums,target);for(int k=0;k<res.size();k++){cout<<"==res[k]:"<<res[k]<<endl;} return 0;
}1-2,两数之和 II - 输入有序数组

方法1:利用字典
class Solution:def twoSum(self, numbers: List[int], target: int) -> List[int]:res_dict = {}for i in range(len(numbers)):value = target - numbers[i]if value in res_dict:return [res_dict[value]+1, i+1]res_dict[numbers[i]] = i方法2:双指针
class Solution:def twoSum(self, numbers, target):left=0right = len(numbers)-1while left<right:sum_= numbers[left]+numbers[right]if sum_==target:return [left+1, right+1]elif sum_<target:left+=1else:right-=1return [-1, -1]sol = Solution()
numbers = [2, 7, 11, 15]
target = 9
res = sol.twoSum(numbers,target)
print('res:',res)
c++实现:
class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {int n = numbers.size();int l=0, r = n-1;while(l < r){if(numbers[l]+numbers[r] > target){r -= 1;}else if(numbers[l] + numbers[r] == target){return {l + 1, r + 1};}else{l += 1;}}return {-1, -1};}
};2.两数相加

思路:开出一个head头,利用一个指针进行遍历,需要注意的是进位
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:head = ListNode(0)new_node = headcarry = 0while l1 and l2:new_node.next =ListNode(l1.val+l2.val+carry)carry = new_node.next.val//10 new_node.next.val = new_node.next.val%10l1 = l1.nextl2= l2.nextnew_node = new_node.next# print(carry)while l1:new_node.next = ListNode(l1.val+carry)carry = new_node.next.val//10new_node.next.val = new_node.next.val%10l1 = l1.nextnew_node = new_node.nextwhile l2:new_node.next = ListNode(l2.val+carry)carry = new_node.next.val//10new_node.next.val = new_node.next.val%10l2 = l2.nextnew_node = new_node.nextif carry:new_node.next = ListNode(carry)return head.nextc++实现:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {ListNode* head = new ListNode(0);ListNode* new_head = head;int carry = 0;while(l1 && l2){new_head->next = new ListNode(l1->val + l2->val + carry);carry = new_head->next->val/10;new_head->next->val = new_head->next->val%10; new_head = new_head->next;l1 = l1->next;l2 = l2->next;}while(l1){new_head->next = new ListNode(l1->val + carry);carry = new_head->next->val/10;new_head->next->val = new_head->next->val%10; new_head = new_head->next;l1 = l1->next;}while(l2){new_head->next = new ListNode(l2->val + carry);carry = new_head->next->val/10;new_head->next->val = new_head->next->val%10; new_head = new_head->next;l2 = l2->next;}if(carry){new_head->next = new ListNode(carry);}return head->next;}
};3.无重复字符的最长子串

思路:滑动窗口,先往右拓展字典进行加1,发现大于1的在往左压缩 python代码
class Solution:def lengthOfLongestSubstring(self, s):n = len(s)left = 0right = 0dict_= {}res = 0while right<n:#往右拓展dict_[s[right]] = dict_.get(s[right], 0)+1#出现就加1while dict_[s[right]]>1:#解决这种两个连续ww的问题"pwwkew" 再次出现往左压缩dict_[s[left]]-=1left+=1res = max(res, right-left+1)right+=1return res# s = "abcabcbb"
# s = "dvdf"
s = "pwwkew"
sol = Solution()
sol.lengthOfLongestSubstring(s)c++代码:
#include <string>
#include <iostream>
#include <vector>
#include <list>
#include <map>
#include <typeinfo>using namespace std;class Solution {
public:int lengthOfLongestSubstring(string s) {int left = 0, right = 0, res = 0;unordered_map<char, int> dict_; //散列表实现 查找更高效int length = s.size();while(right < length){dict_[s[right]]++;while (dict_[s[right]] > 1){dict_[s[left]]--;left++;}right++;res = max(right - left, res);}return res; }
};int main()
{ string s = "abcabc";// Solution sol;// int res;// res= sol.lengthOfLongestSubstring(s);int res;Solution *sol = new Solution();res = sol->lengthOfLongestSubstring(s);delete sol;sol = NULL; cout<<"res:"<<res<<endl;return 0;
}4.寻找两个正序数组的中位数

思路:双指针,走完剩下的在进行合并 时间复杂度o(m+n) 空间复杂度0(m+n)
class Solution:def findMedianSortedArrays(self, nums1, nums2):res = []i, j = 0, 0m, n = len(nums1), len(nums2)while i < m and j < n:if nums1[i] < nums2[j]:res.append(nums1[i])i += 1else:res.append(nums2[j])j += 1print('==res:', res)print('==i:', i)print('==j:', j)if i < m:res.extend(nums1[i:])if j < n:res.extend(nums2[j:])print('==res:', res)if (m+n)%2==0:#偶数return (res[(m+n)//2]+res[(m+n)//2-1])/2else:#奇数return res[(m+n)//2]# nums1 = [1, 1, 3]
# nums2 = [2]
nums1 = [1,2]
nums2 = [3,4]
sol = Solution()
res = sol.findMedianSortedArrays(nums1, nums2)
print(res)c++实现:
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size();int n = nums2.size();int i=0, j=0;vector<double> res;while(i<m && j<n){if(nums1[i]<nums2[j]){res.push_back(nums1[i]);i++;}else{res.push_back(nums2[j]);j++;}}while(i<m){res.push_back(nums1[i]);i++;}while(j<n){res.push_back(nums2[j]);j++;}// for(int i=0;i<res.size(); i++){// cout<<"res:"<<res[i]<<endl;// }if((m+n)%2){return res[(m+n)/2];}else{return (res[(m+n)/2-1] + res[(m+n)/2])*1.0/2.;}return 0.;}
};优化:双指针识别,不用开辟数组空间, 时间复杂度o((m+n)/2) 空间复杂度0(1)
class Solution {
public:double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {//双指针吧int m = nums1.size();int n = nums2.size();int i=0, j=0;float preNum = 0, current = 0;while((i + j) <= (m + n)/2){preNum = current;if((j >= n) || (i < m && nums1[i] < nums2[j])){current = nums1[i];i++;}else{current = nums2[j];j++;}}if((m + n)%2 == 0){return (current + preNum) / 2;}else{return current;}}
};5.最长回文子串

思路:中心枚举
class Solution:def helper(self,left,right,s):while left>=0 and right<len(s) and s[left]==s[right]:left-=1right+=1if len(s[left+1:right])>len(self.res):self.res = s[left+1:right]def longestPalindrome(self, s: str) -> str:self.res = ''for i in range(len(s)):self.helper(i,i,s)self.helper(i,i+1,s)return self.res
c++实现:
class Solution {
public:string res;void help(int left, int right, string& s){while(left >= 0 && right < s.size() && s[left] == s[right]){left--;right++;}left++;right--;if(right - left + 1 > res.size()){res = s.substr(left, right - left + 1);}}string longestPalindrome(string s) {if(s.size() <= 1){return s;}for(int i=1; i<s.size(); i++){help(i-1, i+1, s);help(i-1, i, s);}return res;}
};6,盛最多水的容器
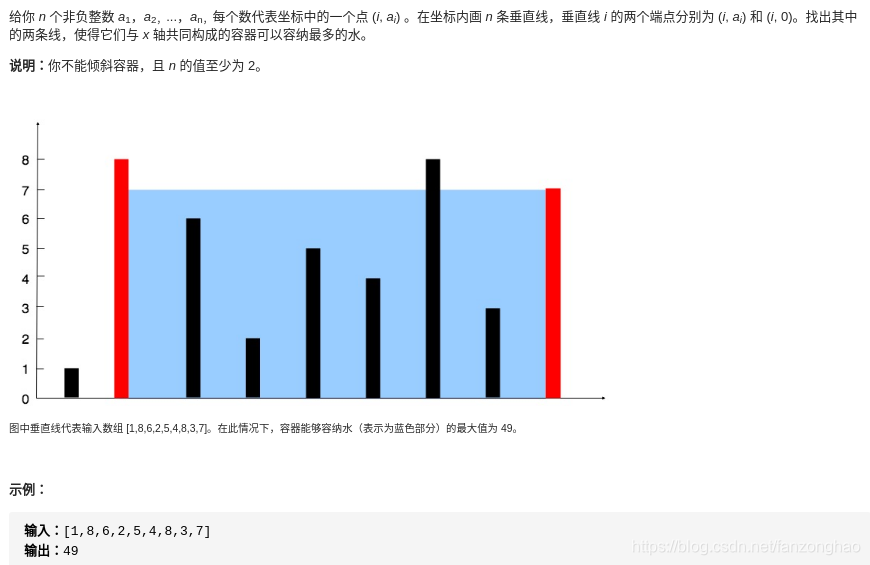
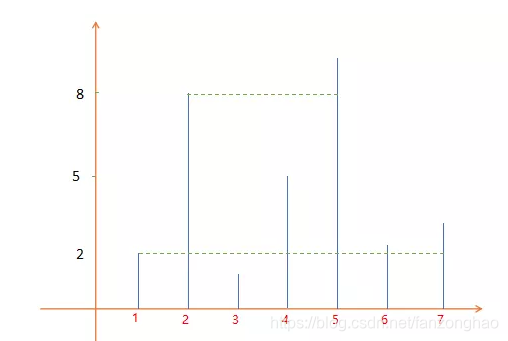
求Max{(j-i) * Min( h(i), h(j) )},
思路:双指针
时间复杂度为 O(n),空间复杂度为 O(1) 。
#解法2
class Solution:def maxarea(self,height):left=0right=len(height)-1max_area=0while left<right:max_area = max(max_area,(right - left) * min(height[left], height[right]))if height[left]<height[right]:left+=1else:right-=1# index_i = left# index_j=rightreturn max_areas=Solution()
height=[2,8,1,5,9,3,4]
max_area=s.maxarea(height)
print(max_area)c++实现:
class Solution {
public:int maxArea(vector<int>& height) {int left = 0;int right = height.size() - 1;int max_area = 0;while(left < right){max_area = max(max_area, min(height[left], height[right])*(right - left)); if(height[left]<height[right]){left++;} else{right--;}}return max_area;}
};7.三数之和

思路1: 固定两数,寻找第三个数,两层循环,最复杂解法,列表比较大时,时间会很长
class Solution:def threeSum(self, nums):""":type nums: List[int]:rtype: List[List[int]]"""result=[]nums.sort()length=len(nums)for i in range(length-1):for j in range(i+1,length):if -(nums[i]+nums[j]) in nums[j+1:]:tmp=[nums[i],nums[j],-(nums[i]+nums[j])]if tmp not in result:result.append(tmp)return result思路2: 双指针,固定一个数,让其余两个数从第一个数+1和尾 向中间靠近,只需要循环一遍
# 双指针:排好序以后,双指针去寻找两数之和等于第一个
class Solution:def threeSum(self, nums):nums = sorted(nums)res = []n = len(nums)print('==nums:', nums)for i in range(n):if i>0 and nums[i]==nums[i-1]:#去除相同的第一个数[-1, 0, 1, 2, -1, -4]continuestart = i + 1end = n - 1# print('==start:', start)# print('==end:', end)while start < end:if nums[i] + nums[start] + nums[end] == 0:res.append([nums[i], nums[start], nums[end]])start += 1end -= 1while start<end and nums[start]==nums[start-1]:# 首部出现连续两个数[-2, 0, 0, 2, 2]start+=1while start<end and nums[end]==nums[end+1]:# 尾部出现连续两个数[-2, 0, 0, 2, 2]end-=1elif (nums[i] + nums[start] + nums[end]) > 0:end -= 1else:start += 1print('==res:', res)return res# nums = [-1, 0, 1, 2, -1, -4]
nums = [-2, 0, 0, 2, 2]
sol = Solution()
sol.threeSum(nums)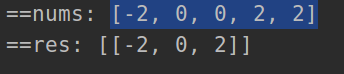
c++实现:
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {vector<vector<int>> res;sort(nums.begin(), nums.end());int n = nums.size();for(int i=0; i<n; i++){if(i>0 && nums[i]==nums[i-1]){continue;}int start = i + 1;int end = n - 1;while(start < end){if(nums[i] + nums[start] + nums[end] == 0){res.push_back({nums[i], nums[start], nums[end]});start++;end--;while(start < end && nums[start]==nums[start-1]){start++;}while(start < end && nums[end]==nums[end+1]){end--;}}else if((nums[i] + nums[start] + nums[end]) > 0){end--;}else{start++;}}}return res;}
};思路3.利用两数之和
class Solution:def twoSum(self, nums, target):res_dict = {}for i in range(len(nums)):value = -target - nums[i]if value in res_dict:self.res.add((target, nums[i], value))res_dict[nums[i]] = idef threeSum(self, nums: List[int]) -> List[List[int]]:self.res = set()nums = sorted(nums)for i in range(len(nums)):if i>0 and nums[i] == nums[i-1]:continueself.twoSum(nums[i+1:], nums[i])return list(self.res)8. 四数之和

思路:也是双指针
class Solution(object):def fourSum(self, nums, target):""":type nums: List[int]:type target: int:rtype: List[List[int]]"""nums = sorted(nums)ans = set()for i in range(len(nums) - 3):#第一层循环到达三个数之前for j in range(i + 1,len(nums) - 2):#最后两个数需要固定start = j+1 end = len(nums)-1while(start < end):temp = nums[i] + nums[j] + nums[start] + nums[end]if temp == target:ans.add((nums[i], nums[j], nums[start], nums[end]))start += 1end -= 1elif temp > target:end -= 1else:start += 1return list(ans)8.电话号码的字母组合

思路:组合问题 用回溯
class Solution:def backtrace(self, digits, track):if len(digits) == 0:#满足终止条件self.res.append(track)returnfor letter in self.phone[digits[0]]:# for循环去遍历选择条件store = track#保存中间结果用于回溯track += letterself.backtrace(digits[1:], track)track = store#恢复中间结果回溯def letterCombinations(self, digits):self.res = []if len(digits) == 0:return self.resself.phone = {'2': ['a', 'b', 'c'],'3': ['d', 'e', 'f'],'4': ['g', 'h', 'i'],'5': ['j', 'k', 'l'],'6': ['m', 'n', 'o'],'7': ['p', 'q', 'r', 's'],'8': ['t', 'u', 'v'],'9': ['w', 'x', 'y', 'z']}self.backtrace(digits, track='')print('==self.res:', self.res)return self.resdigits = "23"
sol = Solution()
sol.letterCombinations(digits)
![]()
9.删除链表的倒数第N个节点

思路:找到链表长度,通过在头结点补充一个节点找到要删除的节点的上一个节点,然后在进行删除
方法1:循环
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:length = 0 node = head#获取链表长度while node:length+=1node= node.next# print(length)curr_length = 0new_head = ListNode(0)new_head.next = headnode2=new_headstop_length = length - n#循环走到要删除节点的前一个节点while stop_length:stop_length-=1node2 = node2.next#跳过要删除的节点即可node2.next = node2.next.nextreturn new_head.next
方法2:递归
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def __init__(self):self.count = 0def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:if not head: return head head.next = self.removeNthFromEnd(head.next, n) # 递归调用self.count += 1 # 回溯时进行节点计数return head.next if self.count == n else head
方法3:双指针 推荐使用
fist 指针与second指针相隔n,这样first跑到尾部,second的下一个节点就是倒数第n个

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:# def __init__(self):# self.count = 0def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:new_head = ListNode(0)new_head.next = headfirst = headsecond = new_headfor i in range(n):first = first.nextwhile first:first = first.nextsecond = second.nextsecond.next = second.next.nextreturn new_head.nextc++实现:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* removeNthFromEnd(ListNode* head, int n) {ListNode* new_head = new ListNode(0);new_head ->next = head;ListNode* first = head;ListNode* second = new_head;for(int i=0;i<n;i++){first = first->next;}while(first){first = first->next;second = second->next;}second->next = second->next->next;return new_head->next;}
};10.有效的括号

思路: 栈
class Solution:def isValid(self, s: str) -> bool:stack= []dict_ = {')':'(','}':'{',']':'[',}for i in range(len(s)):if s[i] in dict_.keys():if len(stack) == 0 or stack[-1] != dict_[s[i]]:return Falseelse:stack.pop()else:stack.append(s[i])return len(stack) == 0c++实现:
class Solution {
public:bool isValid(string s) {map<char, char> dict_;dict_[']'] = '[';dict_['}'] = '{';dict_[')'] = '(';vector<int> stack_;for(int i = 0; i < s.size(); i++){if(dict_.count(s[i]) > 0){if(stack_.empty() || stack_.back() != dict_[s[i]]){return false;}else{stack_.pop_back();}}else{stack_.push_back(s[i]);} }return stack_.empty();}
};11.合并两个排序的链表
思路:引入一个指针头 python实现
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = Noneclass Solution:def mergeTwoLists(self, l1: ListNode, l2: ListNode) -> ListNode:head = ListNode(0)node = headwhile l1 and l2:if l1.val < l2.val:node.next = l1l1 = l1.nextelse:node.next = l2l2 = l2.nextnode = node.nextif l1 is not None:node.next= l1if l2 is not None:node.next= l2return head.nextc++实现:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {ListNode* new_head = new ListNode(0);ListNode* node = new_head;while(l1!=NULL && l2 !=NULL){if(l1->val<l2->val){node->next = l1;l1 = l1->next;}else{node->next = l2;l2 = l2->next; }node = node->next;}if (l1!=NULL){node->next = l1;}if(l2!=NULL){node->next = l2;}return new_head->next;}
};12.括号生成

思路:回溯剪枝

1.左右括号插入数量不能超过n
2.左括号数量大于右括号,就可以插入右括号
# 回溯法:插入数量不超过n
# 可以插入 ) 的前提是 ( 的数量大于 )
class Solution(object):def generateParenthesis(self, n):""":type n: int:rtype: List[str]"""self.res = []self.dfs(n, n, '')return self.resdef dfs(self, left, right, track):if left == 0 and right == 0: # 递归终止条件 左括号与右括号都用完self.res.append(track)returnif left > 0: # 左括号个数store = track #track += '('self.dfs(left - 1, right, track)track = storeif left < right: # 左括号个数大于右括号 此时可以添加右括号# store = tracktrack += ')'self.dfs(left, right - 1, track)# track = storen = 2
sol = Solution()
res = sol.generateParenthesis(n)
print(res)13.合并K个升序链表

思路1:上一题合并两个变成for循环顺序合并
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def mergeTwo(self, l1, l2):if l1 is None:return l2if l2 is None:return l1head = ListNode(0)node = headwhile l1 and l2:if l1.val <l2.val:node.next = l1l1 = l1.nextelse:node.next = l2l2 = l2.nextnode = node.nextif l1:node.next = l1if l2:node.next = l2return head.nextdef mergeKLists(self, lists: List[ListNode]) -> ListNode:ans = Nonefor i in range(len(lists)):ans = self.mergeTwo(ans,lists[i])return ansc++:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergtwo(ListNode* l1, ListNode* l2){if(l1==nullptr){return l2;}if(l2==nullptr){return l1;}ListNode* new_head= new ListNode(0);ListNode* node = new_head;while(l1 && l2){if(l1->val<l2->val){node->next = l1;l1= l1->next;}else{node->next = l2;l2= l2->next;}node = node->next;}if(l1){node->next = l1;}if(l2){node->next = l2;}return new_head->next;}ListNode* mergeKLists(vector<ListNode*>& lists) {ListNode* res = nullptr;for (int i=0;i<lists.size();i++){res = mergtwo(res,lists[i]);}return res;}
};思路2:分治归并1
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def mergeTwo(self, l1, l2):if l1 is None:return l2if l2 is None:return l1head = ListNode(0)node = headwhile l1 and l2:if l1.val <l2.val:node.next = l1l1 = l1.nextelse:node.next = l2l2 = l2.nextnode = node.nextif l1:node.next = l1if l2:node.next = l2return head.nextdef mergeSort(self, lists, left, right):if left==right:return lists[left]middle = left + (right-left)//2# print('== middle:', middle)l1 = self.mergeSort(lists,left,middle)# print('== l1:', l1)l2 = self.mergeSort(lists,middle+1,right)return self.mergeTwo(l1, l2)def mergeKLists(self, lists: List[ListNode]) -> ListNode:# print('==hahah')if len(lists)==0:return Nonereturn self.mergeSort(lists,0,len(lists) - 1)c++实现:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergetwo(ListNode* l1, ListNode* l2){if(l1==nullptr){return l2;}if(l2==nullptr){return l1;}ListNode* new_head= new ListNode(0);ListNode* node = new_head;while(l1 && l2){if(l1->val<l2->val){node->next = l1;l1= l1->next;}else{node->next = l2;l2= l2->next;}node = node->next;}if(l1){node->next = l1;}if(l2){node->next = l2;}return new_head->next;}ListNode* mergesort(vector<ListNode*>& lists,int left, int right){if(left==right){return lists[left];}int middle = left+(right -left)/2;ListNode* l1 = mergesort(lists,left,middle);ListNode* l2 = mergesort(lists,middle+1,right);return mergetwo(l1,l2);}ListNode* mergeKLists(vector<ListNode*>& lists) {// ListNode* res = nullptr;// for (int i=0;i<lists.size();i++){// res = mergtwo(res,lists[i]);// }// return res;if (lists.size()==0){return nullptr;}return mergesort(lists,0,lists.size()-1);}
};思路3:分支归并2 参考排序算法的归并排序 排序算法--(冒泡排序,插入排序,选择排序,归并排序,快速排序,桶排序,计数排序,基数排序)_智障变智能-CSDN博客
class Solution:def mergeTwo(self, l1, l2):if l1 is None:return l2if l2 is None:return l1head = ListNode(0)node = headwhile l1 and l2:if l1.val < l2.val:node.next = l1l1 = l1.nextelse:node.next = l2l2 = l2.nextnode = node.nextif l1:node.next = l1if l2:node.next = l2return head.nextdef mergeSort(self, L):if len(L) <= 1:return L[0]mid = len(L) // 2 l1 = self.mergeSort(L[:mid])l2 = self.mergeSort(L[mid:])return self.mergeTwo(l1, l2)def mergeKLists(self, lists: List[ListNode]) -> ListNode:if len(lists)==0:return Nonereturn self.mergeSort(lists)14-1.下一个排列

思路:
1.要逆序找,这个时候的数最小;
2. 希望下一个数比当前数(递增的拐点)大,
3. 尽量大的幅度是最小的.

# 1.要逆序找,这个时候的数最小;
# 2. 希望下一个数比当前数(递增的拐点)大,
# 3. 尽量大的幅度是最小的class Solution(object):# 交换def reverse(self, nums, left, right):while left < right:nums[left], nums[right] = nums[right], nums[left]left += 1right -= 1return numsdef nextPermutation(self, nums):""":type nums: List[int]:rtype: None Do not return anything, modify nums in-place instead."""# nums = [1, 2, 7, 4, 3, 1]first_index = -1second_index = -1# 先找到逆序的峰值前的第一个点的索引first_indexfor i in range(len(nums) - 2, -1, -1):if nums[i] < nums[i + 1]:first_index = ibreakprint('==first_index:', first_index)# 在找到稍微大于first_index的索引for i in range(first_index, len(nums)):if nums[i] > nums[first_index]:second_index = iprint('==second_index:', second_index)if first_index != -1: # 交换以后 对剩下的进行逆序nums[first_index], nums[second_index] = nums[second_index], nums[first_index]nums = self.reverse(nums, first_index + 1, len(nums) - 1)else: # 说明全逆序nums = self.reverse(nums, 0, len(nums) - 1)return nums# nums = [5, 4, 7, 5, 3, 2]
# nums = [1, 2, 7, 4, 3, 1]
# nums = [1, 2, 3, 8, 5, 7, 6]
nums = [1, 2, 3]
# nums = [3, 2, 1]
# nums=[-2,-1]
# nums=[0]
# nums=[2,2]
# nums=[4,10,4,3,8,9]
sol = Solution()
res = sol.nextPermutation(nums)
print('res:', res)
c++实现:
class Solution {
public:void help(vector<int>& nums, int left, int right ){while(left < right){int temp = nums[left];nums[left] = nums[right];nums[right] = temp;left++;right--;}}void nextPermutation(vector<int>& nums) {int first_index = -1, second_index = -1;int length = nums.size();for (int i = length-2; i>=0; i--){if(nums[i] < nums[i+1]){first_index = i;break;}}if(first_index != -1){for (int i = first_index + 1; i<length; i++){if(nums[i] > nums[first_index]){second_index = i;} }}if (first_index != -1){int temp = nums[first_index];nums[first_index] = nums[second_index];nums[second_index] = temp;help(nums, first_index + 1, length - 1);}else{help(nums, 0, length - 1);}}
};14-2.下一个更大元素 III

思路:和上一题一样,只不过是将int转成string
class Solution:def swap(self, list_str, left, right):while left < right:list_str[left], list_str[right] = list_str[right], list_str[left]left += 1right -= 1return list_strdef nextGreaterElement(self, n: int) -> int:list_n = list(str(n))first_index = -1for i in range(len(list_n) - 2, -1, -1):if list_n[i] < list_n[i + 1]:first_index = ibreakif first_index == -1:return -1second_index = -1for i in range(first_index, len(list_n)):if list_n[i] > list_n[first_index]:second_index = ilist_n[first_index], list_n[second_index] = list_n[second_index], list_n[first_index]list_n = self.swap(list_n, first_index + 1, len(list_n) - 1)value = int(''.join(list_n))if value < (1<<31):return valueelse:return -1c++实现:
class Solution {
public:void reverse(string& str_n, int left, int right){while(left < right){char temp = str_n[left];str_n[left] = str_n[right];str_n[right] = temp;left++;right--;}}int nextGreaterElement(int n) {string str_n = to_string(n);int first_index = -1;for(int i = str_n.size() - 2; i >= 0; i--){if(str_n[i] < str_n[i+1]){first_index = i;break;}}if(first_index == -1){return -1;}int second_index = -1;for(int i = first_index + 1; i < str_n.size(); i++){if (str_n[i] > str_n[first_index]){second_index = i;}}char temp = str_n[first_index];str_n[first_index] = str_n[second_index];str_n[second_index] = temp;reverse(str_n, first_index + 1, str_n.size() - 1);long value = atol(str_n.c_str());if(value > INT_MAX){return -1;}else{return value;}}
};15-1.给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。

思路:利用栈将括号左半部分先入栈,后半部分进行判断并匹配
class Solution:def isValid(self, s):stack= []for i in range(len(s)):if s[i] == '(' or s[i] == '[' or s[i] == '{':stack.append(s[i])elif len(stack) and s[i] == ']' and stack[-1] == '[':stack.pop()elif len(stack) and s[i] == ')' and stack[-1] == '(':stack.pop()elif len(stack) and s[i] == '}' and stack[-1] == '{':stack.pop()else:return Falsereturn len(stack)==0sol = Solution()
s = '()'
# s = '()[]{}'
res = sol.isValid(s)
print('res:', res)
class Solution:def isValid(self, s):stack= []dict_={')':'(',']':'[','}':'{'}for i in range(len(s)):if s[i] in dict_.keys():if len(stack)==0 or stack[-1] != dict_[s[i]]:return Falseelse:stack.pop()else:stack.append(s[i])return len(stack)==0sol = Solution()
s = '()'
# s = '()[]{}'
res = sol.isValid(s)
print('res:', res)15-2:最长有效括号

思路:先利用栈存储相邻括号的索引,在用双指针做聚类class Solution:def longestValidParentheses(self, s: str) -> int:stack = []res = []for i in range(len(s)):if s[i] == '(':stack.append(i)if stack and s[i] == ')':res.append(stack.pop())res.append(i)print(res)res = sorted(res)left, right = 0, 0# fin_res = []ans = 0while right < len(res):right = left + 1while right < len(res) and res[right] - res[right - 1] == 1:right += 1# fin_res.append([left, right-1])ans = max(right - left, ans)left = rightprint(ans)return ans# s = "(()"
# s = "()(()"
# s = ")()())"
s = "()(())"
sol = Solution()
sol.longestValidParentheses(s)

16-1.搜索插入位置
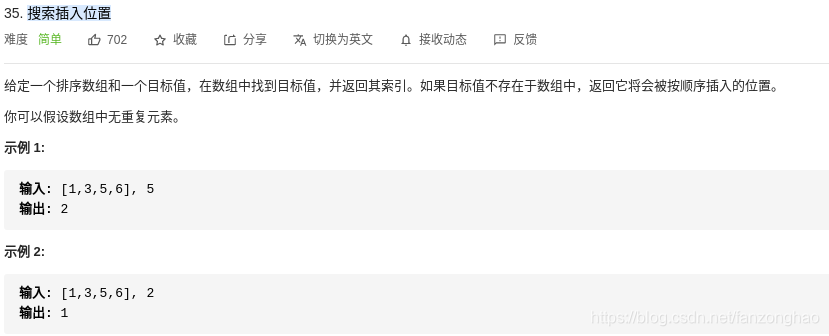
思路:二分查找 利用二分法不断逼近目标数的索引
class Solution:def searchInsert(self, nums: List[int], target: int) -> int:#二分查找left = 0right = len(nums)-1while left<=right:middle = left + (right - left )//2# print(middle)if nums[middle]==target:return middleelif nums[middle]>target:right = middle - 1else:left=middle+1return left16-2.在排序数组中查找元素的第一个和最后一个位置

思路1:双指针,时间复杂度O(n)
#O(n)
class Solution:def searchRange(self, nums, target):left,right = 0,len(nums)-1while left < right:if nums[left]==target and nums[right]==target:return [left,right]elif nums[left]<target:left+=1else:right -= 1return [-1,-1]nums = [5,7,7,8,8,10]
target = 8
sol = Solution()
res = sol.searchRange(nums,target)
print(res)思路2:二分查找法,时间复杂度O(logn)
重点是找到左边界和右边界
class Solution:def serachLeft(self, nums, target):left, right = 0, len(nums) - 1while left <= right:middle = left + (right - left) // 2if nums[middle] < target:left = middle+1else:right = middle-1return leftdef serachRight(self, nums, target):left, right = 0, len(nums) - 1while left <= right:middle = left + (right - left) // 2if nums[middle] <= target:#加个等于符号 这样left就可以找到最后一个left = middle + 1else:right = middle - 1return left-1def searchRange(self, nums, target):left = self.serachLeft(nums, target)# print('==left:', left)right = self.serachRight(nums, target)# print('==right:', right)if left<=right:return [left,right]else:return [-1, -1]# nums = [5, 7, 7, 8, 8, 8]
nums = [5, 7, 7, 9, 9, 9]
target = 8
sol = Solution()
sol.searchRange(nums, target)
16-3.搜索旋转排序数组

思路:判断中值和右值的关系来决定是否是有序的,通过缩短为有序数组 在进行二分法查找
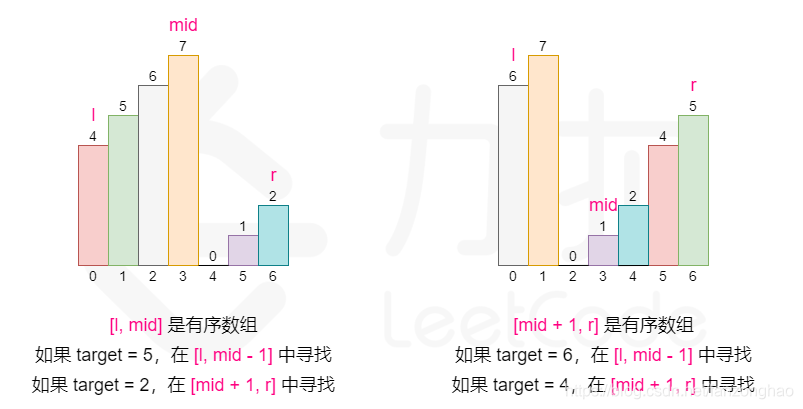
class Solution:def search(self, nums: List[int], target: int) -> int:left,right=0,len(nums)-1while left<=right:middle = left + (right-left)//2if nums[middle]==target:return middleif nums[middle]<nums[right]:#从middle到right是有序的if nums[middle]<target<=nums[right]:left =middle+1else:right = middle-1else:#从left到middle是有序的if nums[left]<=target<nums[middle]:right=middle-1else:left = middle+1return -1
16-4.搜索旋转排序数组 II

思路:判断左右两个子序 注意需要去重 避免对顺序造成的干扰
class Solution:def search(self, nums: List[int], target: int) -> bool:left,right = 0,len(nums)-1while left<=right:middle = left+(right-left)//2if nums[middle]==target:return Trueif (nums[middle] == nums[left] == nums[right]):#去除边界重复值left += 1right -= 1elif nums[middle]>=nums[left]:#left到middle有序if nums[left]<=target<nums[middle]:right = middle - 1else:left=middle+1else:#middle 到right有序# print('==hahhahha====')# print('==left:', left)# print('==middle:', middle)if nums[middle]<target<=nums[right]:left = middle + 1else:right = middle - 1return False16-5.寻找旋转排序数组中的最小值

思路:
class Solution:def findMin(self, nums: List[int]) -> int:# return min(numbers)left, right = 0, len(nums) - 1while left < right:middle = left + (right - left) // 2if nums[middle] < nums[right]:#说明middle是最小值右侧元素right = middleelif nums[middle] > nums[right]:#说明middle是最小值左侧元素left = middle + 1else:right -= 1 #相当就没法判断 采取保守right-1即可# print('==left:', left)# print('===numbers[left]', numbers[left])return nums[left]17-1:组合总和I

思路:组合排列问题 回溯法
由于可以选2,2,3 不可以再选,3,2,2所以用view限定重复是不行的,还要加上start索引
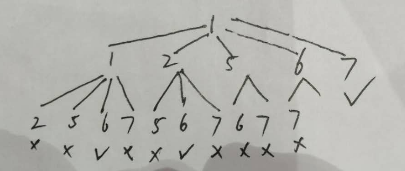
class Solution:def backtrace(self, candidates, target, start, track):# #终止条件if target == 0:self.res.append(track)returnfor i in range(start, len(candidates)):if candidates[i] > target:continue# if (i > 0 and candidates[i] == candidates[i - 1]):# continue # 去掉重复的store = track.copy()track.append(candidates[i])#其中值满足选择条件# print('==track.copy():', track.copy())self.backtrace(candidates, target - candidates[i], i, track) # 回溯track = store # 撤销选择def combinationSum(self, candidates, target):self.res = []candidates = sorted(candidates)self.backtrace(candidates, target, 0, track=[])return self.res# candidates = [2,3,6,7]
# target = 7
candidates = [2,3,5]
target = 8
sol = Solution()
res = sol.combinationSum(candidates, target)
print('res:', res)
c++实现:
class Solution {
public:vector <vector<int>> res;void backtrace(vector<int>& candidates, int target, int start, vector<int>& track){if(target == 0){res.push_back(track);return;}for(int i = start; i < candidates.size(); i++){if(candidates[i] > target){continue;}track.push_back(candidates[i]);backtrace(candidates, target - candidates[i], i, track);track.pop_back();}}vector<vector<int>> combinationSum(vector<int>& candidates, int target) {vector<int> track;backtrace(candidates, target, 0, track);return res;}
};17-2.组合总和 II

思路:注意与17-1的差别,不能重复选数字,故通过排序方便进行剪枝.
class Solution:def backtrace(self, candidates, target, start, track):# #终止条件if target == 0:self.res.append(track)returnfor i in range(start, len(candidates)):if candidates[i] > target:continueif (i > start and candidates[i] == candidates[i - 1]):continue # 去掉重复的store = track.copy()track.append(candidates[i])# print('==track.copy():', track.copy())self.backtrace(candidates, target - candidates[i], i + 1, track) # 回溯track = store # 撤销选择def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:self.res = []candidates = sorted(candidates)self.backtrace(candidates, target, 0, track=[])return self.rescandidates = [10, 1, 2, 7, 6, 1, 5]
# candidates = [1, 7, 1]
target = 8
sol = Solution()
res = sol.combinationSum2(candidates, target)
print('res:', res)
c++实现:
class Solution {
public:vector<vector<int>> res;void backtrace(vector<int>& candidates, int target, int start, vector<int>& track){if(target == 0){res.push_back(track);}for(int i = start; i < candidates.size(); i++){if(target < candidates[i]){continue;}if(i > start && candidates[i] == candidates[i-1]){continue;}track.push_back(candidates[i]);backtrace(candidates, target - candidates[i], i + 1, track);track.pop_back();}}vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {sort(candidates.begin(), candidates.end());vector<int> track;backtrace(candidates, target, 0, track);return res;}
};18-1,盛最多水的容器


求Max{(j-i) * Min( h(i), h(j) )},
height=[2,8,1,5,9,3,4]
暴力法: 超出时间限制
#解法1
class Solution:def maxarea(self,height):max_area=0for i in range(len(height)-1):for j in range(i+1,len(height)):if (j-i)*min(height[i],height[j])>max_area:max_area=(j-i)*min(height[i],height[j])index_i=iindex_j=jreturn index_i,index_j,max_areas=Solution()
height=[2,8,1,5,9,3,4]
i,j,max_area=s.maxarea(height)
print(i,j,max_area)分析:暴力法时间复杂度为O(n2),想想看,
-
如果 h(7) >= h(1),我们还有必要再遍历h(6),h(5),...,h(2)吗,其实不用,这便是暴力算法的冗余之处,多做了很多次无用的遍历,i = 1这趟遍历中,最大面积一定为 (7-1) * h(1) ;
-
如果 h(7) < h(1),我们再尝试h(6),如果h(6)>=h(1),那么在i = 1这趟遍历中的面积最大为(6-1) * h(1),没必要再试h(5)了,依次这样下去。
动态规划:
-
面积最大值初始值设定 maxarea;
-
i, j 分别指向索引两头,动态交替地调整 i, j ,进而尝试取得较大的相对高度,这个调整的策略是关键,同时,更新目标函数即面积的最大值,如果大于maxarea,则更新;
-
直到 i > j 为止;
-
返回最大值法
时间复杂度为 O(n),空间复杂度为 O(1) 。
#解法2
class Solution:def maxarea(self,height):left=0right=len(height)-1max_area=0while left<right:max_area = max(max_area,(right - left) * min(height[left], height[right]))if height[left]<height[right]:left+=1else:right-=1# index_i = left# index_j=rightreturn max_areas=Solution()
height=[2,8,1,5,9,3,4]
max_area=s.maxarea(height)
print(max_area)18-2:接雨水

思路1.暴力法 对于i处能存的水,向右向左分别找到最大的值,在取这两值中的最小值减去此刻的值就是能存的水,超时O(n^2)
class Solution:def trap(self, height):res = 0n = len(height)for i in range(1, n):print('==i:', i)left_max, right_max = 0, 0for j in range(i, -1, -1):#往左搜索left_max = max(left_max, height[j])for j in range(i, n):#往右搜索right_max = max(right_max, height[j])print('==left_max:', left_max)print('==right_max:', right_max)res +=min(right_max, left_max) - height[i]print('res:', res)return resheight = [0,1,0,2,1,0,1,3,2,1,2,1]
sol = Solution()
sol.trap(height)思路2.优化,双指针
#某个位置i处,它能存的水,取决于它左右两边(left_max,right_max)的最大值中较小的一个。
#对于位置left而言,它左边最大值一定是left_max,右边最大值“大于等于”right_max,
# 这时候,如果left_max<right_max成立,那么它就知道自己能存多少水了。
# 无论右边将来会不会出现更大的right_max,都不影响这个结果。
# 所以当left_max<right_max时,我们就希望去处理left下标,反之,我们希望去处理right下标。O(n)class Solution:def trap(self, height):left,right =0,len(height)-1left_max,right_max =0,0res = 0while left<=right:if left_max <right_max:res+=max(0, left_max - height[left])left_max = max(left_max, height[left])left+=1else:res += max(0, right_max - height[right])right_max = max(right_max, height[right])right -= 1print('==res:', res)return resheight = [0,1,0,2,1,0,1,3,2,1,2,1]
sol = Solution()
sol.trap(height)c++实现:
class Solution {
public:int trap(vector<int>& height) {int left = 0, right = height.size() - 1;int left_max = 0, right_max = 0;int res = 0;while(left <= right){if(left_max < right_max){res += max(0, left_max - height[left]);left_max = max(height[left], left_max);left++;}else{res += max(0, right_max - height[right]);right_max = max(height[right], right_max);right--;}}return res;}
};思路3:动态规划
开出两个数组,一个用于统计坐边最大值,一个用于统计右边最大值,这样最终该点的雨水就是当前点的短板减去当前值。
class Solution:def trap(self, height: List[int]) -> int:length = len(height)if length == 0:return 0left_max = [0 for i in range(length)]left_max[0] = height[0]right_max = [0 for i in range(length)]right_max[-1] = height[-1]for i in range(1, length):left_max[i] = max(left_max[i-1], height[i])for i in range(length-2, -1, -1):right_max[i] = max(right_max[i + 1], height[i])res = 0for i in range(length):res += min(left_max[i], right_max[i]) - height[i]return resc++实现 :
class Solution {
public:int trap(vector<int>& height) {int res = 0;int length = height.size();if (length == 0){return res;}vector<int> left_max(length, 0);vector<int> right_max(length, 0);left_max[0] = height[0];right_max[length-1] = height[length-1];for (int i=1; i<length; i++){left_max[i] = max(left_max[i-1], height[i]);}for (int i=length-2; i>=0; i--){right_max[i] = max(right_max[i+1], height[i]);}for (int i=0; i<length; i++){res += min(right_max[i], left_max[i]) - height[i];}return res;}
};19-1.不重复元素全排列 全排列

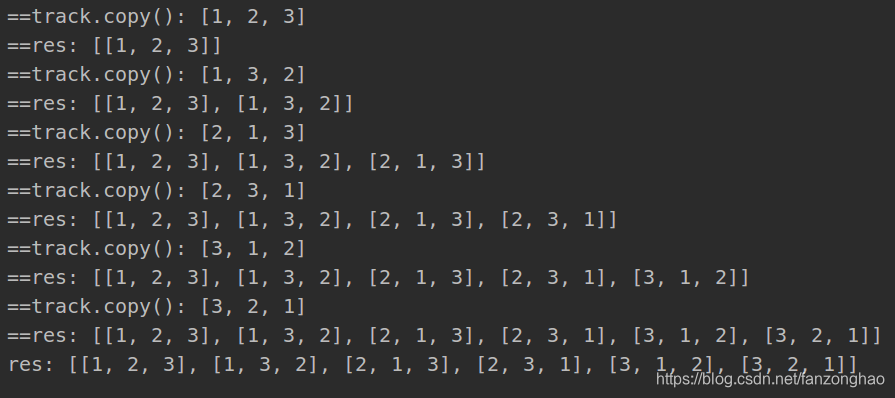
class Solution:def backtrace(self, nums, view, track):#终止条件if len(track)==len(nums):self.res.append(track)returnfor i in range(len(nums)):#满足选择条件if view[i]:#出现元素跳过continue# if i>0 and nums[i] == nums[i-1] and view[i-1]==0:#重复元素跳过# continuestore = track.copy()track.append(nums[i])print('track:', track)view[i] = 1self.backtrace(nums, view, track)track = store# 撤销选择view[i] = 0# 撤销选择def permuteUnique(self, nums):nums = sorted(nums)#排序方便剪枝self.res = []self.backtrace(nums, view=[0]*len(nums), track=[])return self.resnums = [1,2,3]
# nums = [1, 2, 3]
sol = Solution()
res=sol.permuteUnique(nums)
print('res:', res)

c++实现:
class Solution {
public:vector<vector<int>> res;void backtrace(vector<int>& view, vector<int>& track, vector<int>& nums){if(track.size() == nums.size()){res.push_back(track);return ;}for(int i=0; i<nums.size(); i++){if(view[i]){continue;}track.push_back(nums[i]);view[i] = 1;backtrace(view, track, nums);track.pop_back();view[i] = 0;}}vector<vector<int>> permute(vector<int>& nums) {int size = nums.size();vector<int> view(size, 0);vector<int> track;backtrace(view, track, nums);return res;}
};
19-2.重复元素全排列 全排列 II

思路:与上题相比要注意的是剪枝
class Solution:def backtrace(self, nums, view, track):#终止条件if len(track)==len(nums):self.res.append(track)returnfor i in range(len(nums)):#满足选择条件if view[i]:#出现元素跳过continueif i>0 and nums[i] == nums[i-1] and view[i-1]==0:#重复元素跳过continuestore = track.copy()track.append(nums[i])print('track:', track)view[i] = 1self.backtrace(nums, view, track)track = store# 撤销选择view[i] = 0# 撤销选择def permuteUnique(self, nums):nums = sorted(nums)#排序方便剪枝self.res = []self.backtrace(nums, view=[0]*len(nums), track=[])return self.resnums = [1, 1, 2]
# nums = [1, 2, 3]
sol = Solution()
res=sol.permuteUnique(nums)
print('res:', res)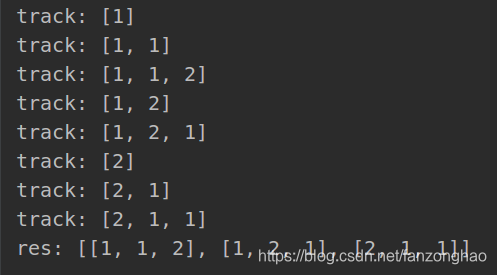
c++实现:
class Solution {
public:vector<vector<int>> res;void backtrace(vector<int>& nums, vector<int>& view, vector<int>& track){if(track.size() == nums.size()){res.push_back(track);return;}for(int i = 0; i < nums.size(); i++){if(view[i]){continue;}if(i > 0 && nums[i] == nums[i-1] && view[i-1] == 0){continue;}view[i] = 1;track.push_back(nums[i]);backtrace(nums, view, track);view[i] = 0;track.pop_back();}}vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end());vector<int> view(nums.size(), 0);vector<int> track;backtrace(nums, view, track);return res;}
};19-3.有重复字符串的排列组合

解法二示意:
class Solution:def help(self, S, view, track):if len(S) == len(track):self.res.append(track)returnfor i in range(len(S)):if view[i]:#出现元素跳过continueif i>0 and S[i] == S[i-1] and view[i-1]==0:#重复字符剪枝continuestore = tracktrack += S[i]view[i] = 1self.help(S, view, track)track = storeview[i] = 0def permutation(self, S: str) -> List[str]:S = sorted(S)self.res = []self.help(S, [0]*len(S), '')return self.res
19-4.二进制手表
可看成全排列找灯问题
class Solution:def readBinaryWatch(self, num):hash_code = {0:1, 1:2, 2:4, 3:8, 4:1, 5:2, 6:4, 7:8, 8:16, 9:32}time_ = {'first':0, 'second':0}res = []def backtrace(num, start, time_):if num == 0:#终止条件剩下0盏灯 此时保存结果if (time_['first'] > 11 or time_['second'] > 59): #判断合法性returnhour = str(time_['first'])minute = str(time_['second'])# print('==hour,minute:', hour, minute)# if hour=='0' and minute=='8':# assert 1==0if len(minute) == 1:minute = '0'+minuteres.append(hour+':'+minute)returnfor i in range(start, 10):#找出符合的if (time_['first'] > 11 or time_['second'] > 59): # 判断合法性continue#保存状态 用于恢复store = time_.copy()if i<4:time_['first'] += hash_code[i]#对小时数进行操作else:time_['second'] += hash_code[i]#对分钟数进行操作#进入下一层,注意下一层的start是i+1,即从当前灯的下一盏开始backtrace(num-1, i+1, time_)time_ = store#恢复状态backtrace(num, 0, time_)return res
n = 1
sol = Solution()
res = sol.readBinaryWatch(n)
print('res:', res)![]()
19-5.找子集(不含重复元素)

思路:回溯,注意的是选择过的数要跳过
#子集问题class Solution:def backtrace(self, nums, start, track):print('==track:', track)self.res.append(track.copy())#满足选择条件print('==self.res:', self.res)for i in range(start, len(nums)):store = track.copy()track.append(nums[i])#做选择self.backtrace(nums, i+1, track)#回溯track = store#撤销def subsets(self, nums):nums = sorted(nums)#排序 方便进行剪枝self.res = []self.backtrace(nums, start=0, track = [])return self.resnums = [1, 2, 3]
sol = Solution()
res = sol.subsets(nums)
print('res:', res)
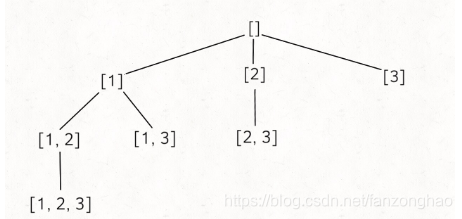
可看出先找到最左边[]->[1]->[1,2]->[1,2,3]然后撤销选择回到上一层变成[]->[1]->[1,2]->[1,2,3]->[1,3],然后在上一层........
19-6.找子集(含重复元素)

思路:回溯注意与上一题的区别在于含有重复元素,需要过滤掉
class Solution:def backtrace(self, nums, view, start, track):self.res.append(track.copy())#满足选择条件for i in range(start, len(nums)):if view[i]:#出现元素跳过continueif i>0 and nums[i] == nums[i-1] and view[i-1]==0:#重复元素跳过continuestore = track.copy()track.append(nums[i])view[i] = 1self.backtrace(nums, view, i + 1, track)#回溯track = store#撤销view[i] = 0#撤销def subsetsWithDup(self, nums):nums = sorted(nums)#排序 方便进行剪枝self.res = []self.backtrace(nums, view=len(nums)*[0], start=0, track=[])return self.resnums = [1, 2, 2]
# nums = [1, 2, 3]
sol = Solution()
res = sol.subsetsWithDup(nums)
print('res:', res)c++实现:
class Solution {
public:vector<vector<int>> res;void backtrace(vector<int>& nums, vector<int>& view, int start, vector<int>& track){res.push_back(track);for(int i = start; i < nums.size(); i++){if(view[i]){continue;}if(i > 0 && nums[i] == nums[i - 1] && view[i-1] == 0){continue;}track.push_back(nums[i]);view[i] = 1;backtrace(nums, view, i + 1, track);view[i] = 0;track.pop_back();}}vector<vector<int>> subsetsWithDup(vector<int>& nums) {sort(nums.begin(), nums.end());int n = nums.size();vector<int> view(n, 0);vector<int> track;backtrace(nums, view, 0, track);return res;}
};19-7.组合问题
例如输入n=4,k=2,输出[[1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4]]
#组合问题
class Solution:def readBinaryWatch(self, n, k):res = []track= []if k<=0 or n<=0:return resdef backtrace(n, k, start, track):if len(track) == k:#终止条件 长度等于kprint('==track.copy():', track.copy())res.append(track.copy())print('==res:', res)returnfor i in range(start, n+1):#找出符合的 选择条件#保存状态 用于恢复store = track.copy()track.append(i)#进入下一层,注意下一层的start是i+1backtrace(n, k, i+1, track)track = store#恢复状态backtrace(n, k, 1, track)return res
n = 4
k = 2
sol = Solution()
res = sol.readBinaryWatch(n, k)
print('res:', res)

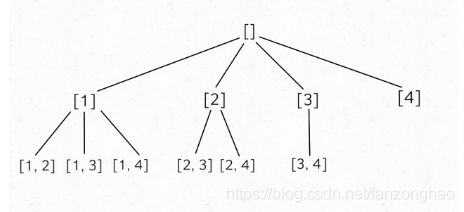
可看出k 限制了树的高度,n 限制了树的宽度,:先找到最左边[1,2]->[1,3]->[1,4]然后撤销选择回到上一层变成[1,2]->[1,3]->[1,4]->[2,3]->[2,4],然后在上一层........
20.旋转图像

思路1:
旋转后的倒数第几列是旋转前的正数第几行
m=[['a','b','c','d'],['e','f','g','h'],['i','j','k','l'],['m','n','o','p']]
n=len(m)
res=[[0]*n for _ in range(n)]
print(res)
for i in range(n):row=m[i]#第i行print(row)ncol=n-i-1#第n-i-1列for j in range(len(row)):res[j][ncol]=row[j]
print(res)
思路2:顺时针旋转90度==转置矩阵+每一行逆序
class Solution:def rotate(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""h = len(matrix)w= len(matrix[0])for i in range(h):for j in range(i+1,w):matrix[i][j],matrix[j][i] = matrix[j][i], matrix[i][j]for i in range(h):matrix[i]=matrix[i][::-1]# print(matrix)return matrix
c++实现:
class Solution {
public:void rotate(vector<vector<int>>& matrix) {int h = matrix.size();int w = matrix[0].size();for(int i = 0; i < h; i++){for(int j = i + 1; j < w; j++){int temp = matrix[i][j];matrix[i][j] = matrix[j][i];matrix[j][i] = temp;}}for(int i = 0; i < h; i++){int j = 0;while(j < w/2){int temp = matrix[i][j];matrix[i][j] = matrix[i][w-j-1];matrix[i][w-j-1] = temp;j++;}}return;}
};21.字母异位词分组

思路1:对排序的字符进行hash表示,自然key值相同的就是异构词,用python字典
#hash
class Solution:def groupAnagrams(self, strs):dict_ = {}for st in strs:key = ''.join(sorted(st))if key not in dict_:dict_[key] = [st]else:dict_[key].append(st)# print('==dict_:', dict_)# print(list(dict_.values()))return list(dict_.values())strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
sol = Solution()
sol.groupAnagrams(strs)思路2:hash,用collections.defaultdict
import collections
class Solution:def groupAnagrams(self, strs):mp = collections.defaultdict(list)print('init mp:', mp)for st in strs:key = "".join(sorted(st))mp[key]. append(st)print('===mp',mp)return mp
strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
sol = Solution()
sol.groupAnagrams(strs)
22.最大子序和

1.修改nums
class Solution(object):def maxSubArray(self, nums):""":type nums: List[int]:rtype: int"""for i in range(1,len(nums)):nums[i]+=max(nums[i-1],0)return max(nums)a=[ 0, -2, 3, 5, -1, 2]
sol=Solution()
res=sol.maxSubArray(a)
print('res:',res)![]()
2.借助一个变量
class Solution:def maxSubArray(self, nums: List[int]) -> int:value = nums[0]res = nums[0]for i in range(1, len(nums)):value = max(nums[i], nums[i]+value)res = max(res, value)return resc++实现:
class Solution {
public:int maxSubArray(vector<int>& nums) {int length = nums.size();if(length < 1){return 0;}int value = nums[0];int res = nums[0];for(int i = 1; i < length; i++){value = max(nums[i], nums[i] + value);res = max(value, res);}return res;}
};23.跳跃游戏

方法1:贪心算法
思路:需要更新最长距离
class Solution:def canJump(self, nums: List[int]) -> bool:贪心算法most_dis = 0for i in range(len(nums)):if i <= most_dis:most_dis = max(most_dis, nums[i] + i)if most_dis >= len(nums) - 1:return Truereturn Falsec++实现:
class Solution {
public:bool canJump(vector<int>& nums) {int most_length = 0;for(int i = 0; i < nums.size(); i++){if(i <= most_length){most_length = max(nums[i] + i, most_length);}if(most_length >= nums.size() - 1){return true;}}return false;方法2:动态规划 需要注意的是 需要实时更新距离
class Solution(object):def canJump(self, nums):""":type nums: List[int]:rtype: bool"""opt = [False]*len(nums)opt[0] = Truefor i in range(1,len(nums)):opt[i] = opt[i-1] and nums[i-1] > 0nums[i] = max(nums[i], nums[i-1]-1)#更新nums 最大距离return opt[-1]c++实现:
class Solution {
public:bool canJump(vector<int>& nums) {int n = nums.size();vector<bool> opt(n, false);opt[0] = true;for(int i = 1; i < n; i++){opt[i] = opt[i - 1] && nums[i-1] >= 1;nums[i] = max(nums[i - 1] - 1, nums[i]);}return opt[n-1];}
};24.合并区间

思路1:不断合并更新
class Solution:def merge(self, intervals):intervals = sorted(intervals, key=lambda x:(x[0], x[-1]))index = 0while index < len(intervals) - 1:if intervals[index][-1] >= intervals[index + 1][0]:intervals[index][-1] = max(intervals[index + 1][-1], intervals[index][-1])intervals.pop(index + 1)else:index += 1print('=intervals:', intervals)return intervalsintervals = [[1, 3], [2, 6], [8, 10], [15, 18]]
# intervals = [[1,4],[0,4]]
sol = Solution()
sol.merge(intervals)思路2:开出新列表用于存储满足条件的数
class Solution:def merge(self, intervals):intervals= sorted(intervals,key= lambda x:(x[0],x[-1]))print('==intervals:', intervals)res = [intervals[0]]for i in range(1, len(intervals)):if intervals[i][0]<=res[-1][-1]:res[-1][-1] = max(intervals[i][-1],res[-1][-1])else:res.append(intervals[i])print('==res:', res)return res# intervals = [[1,3],[2,6],[8,10],[15,18]]
intervals = [[1,4],[2,3]]
sol = Solution()
sol.merge(intervals)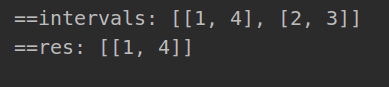
c++实现:
class Solution {
public:vector<vector<int>> merge(vector<vector<int>>& intervals) {if(intervals.size() == 0){return {};}sort(intervals.begin(), intervals.end());vector<vector<int>> merges={intervals[0]};for(int i=1; i<intervals.size(); i++){if(merges.back()[1] >= intervals[i][0]){merges.back()[1] = max(intervals[i][1], merges.back()[1]);}else{merges.push_back(intervals[i]);}}return merges;}
};25.不同路径

思路:动态规划 dp[i][j] = dp[i-1][j]+dp[i][j-1]
import numpy as np
#思路:dp[i][j] = dp[i-1][j]+dp[i][j-1]
class Solution:def uniquePaths(self, m, n):dp = [[0 for i in range(n)] for j in range(m)]for i in range(m):dp[i][0] = 1for i in range(n):dp[0][i] = 1print('==np.array(dp):', np.array(dp))for i in range(1,m):for j in range(1,n):dp[i][j] = dp[i-1][j]+dp[i][j-1]print(np.array(dp))return dp[-1][-1]m = 3
n = 2
sol = Solution()
sol.uniquePaths(m, n)
c++实现:
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for(int i = 0; i < n; i++){dp[0][i] = 1;}for(int i = 0; i < m; i++){dp[i][0] = 1;}for(int i = 1; i < m; i++){for(int j = 1; j < n; j++){dp[i][j] = dp[i-1][j] + dp[i][j-1];} }return dp[m - 1][n - 1];}
};26.最小路径和

思路:动态规划 dp[i][j] = min(dp[i-1][j],dp[i][j-1])+v[i][j]
import numpy as np
#dp[i][j] = min(dp[i-1][j],dp[i][j-1])+v[i][j]
class Solution:def minPathSum(self, grid):h = len(grid)w = len(grid[0])dp = [[0 for i in range(w)] for j in range(h)]dp[0][0] = grid[0][0]for i in range(1, h):dp[i][0] = dp[i-1][0]+grid[i][0]for i in range(1, w):dp[0][i] = dp[0][i-1]+grid[0][i]print('==np.array(dp):\n', np.array(dp))for i in range(1, h):for j in range(1, w):dp[i][j] = min(dp[i-1][j],dp[i][j-1])+grid[i][j]print('==np.array(dp):\n', np.array(dp))return dp[-1][-1]
grid = [[1,3,1],[1,5,1],[4,2,1]]
sol = Solution()
sol.minPathSum(grid)

27.爬楼梯

思路1:dp
class Solution:def climbStairs(self, n: int) -> int:if n<3:return ndp = [0]*(n+1)dp[1] = 1dp[2] = 2for i in range(3, n+1):dp[i] = dp[i-1]+dp[i-2]return dp[-1]思路2:变量
class Solution:def climbStairs(self, n: int) -> int:if n<3:return na = 1b = 2for i in range(3, n+1):a, b = b, a + breturn bc++实现:
class Solution {
public:int climbStairs(int n) {if(n < 3){return n;}int a = 1, b = 2;for(int i = 3; i < n+1; i++){int temp = a;a = b;b += temp;}return b;}
};28.编辑距离
编辑距离,又称Levenshtein距离(莱文斯坦距离也叫做Edit Distance),是指两个字串之间,由一个转成另一个所需的最少编辑操作次数,如果它们的距离越大,说明它们越是不同。许可的编辑操作包括将一个字符替换成另一个字符,插入一个字符,删除一个字符。
mat[i+1,j]+1表示增加操作
d[i,j+1]+1 表示删除操作
d[i,j]+temp表示替换操作,其中temp取0或1

import numpy as np# 相等的情况dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]+1, dp[i][j-1]+1)
# 不相等的情况dp[i][j] = min(dp[i-1][j-1]+1, dp[i-1][j]+1, dp[i][j-1]+1)
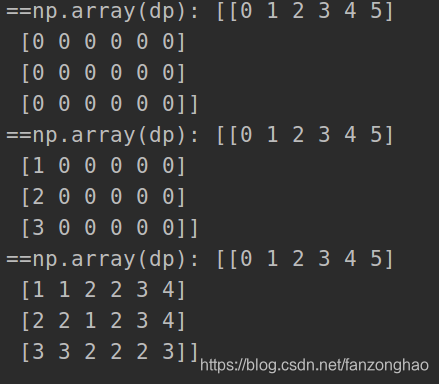
class Solution:def minDistance(self, word1, word2):dp = [[0 for i in range(len(word1) + 1)] for i in range(len(word2) + 1)]for i in range(len(word1) + 1):dp[0][i] = iprint('==np.array(dp):', np.array(dp))for i in range(len(word2) + 1):dp[i][0] = iprint('==np.array(dp):', np.array(dp))for i in range(len(word2)):for j in range(len(word1)):if word2[i] == word1[j]:dp[i+1][j+1] = dp[i][j]else:dp[i+1][j+1] = min(dp[i][j]+1, dp[i][j+1]+1, dp[i+1][j]+1)print('==np.array(dp):', np.array(dp))return dp[-1][-1]word1 = "horse"
word2 = "ros"
sol = Solution()
sol.minDistance(word1, word2)
c++实现:
class Solution {
public:int minDistance(string word1, string word2) {int h = word1.size();int w = word2.size();vector<vector<int>> opt(h + 1, vector<int>(w + 1, 0));for(int i = 0; i < h; i++){opt[i + 1][0] = i + 1;}for(int j = 0; j < w; j++){opt[0][j + 1] = j + 1;}for(int i = 0; i < h; i++){for (int j = 0; j < w; j++){if(word1[i] == word2[j]){opt[i + 1][j + 1] = opt[i][j];}else{opt[i + 1][j + 1] = min(opt[i][j] + 1, min(opt[i + 1][j] + 1, opt[i][j + 1] + 1));}}}return opt[h][w];}
};29.颜色分类

思路1:单指针法:先将0进行交换放在第一位,再将1进行交换放在0后面
# 单指针法:先将0进行交换放在第一位,再将1进行交换放在0后面
class Solution:def sortColors(self, nums):"""Do not return anything, modify nums in-place instead."""# 先将0进行交换放在第一位start = 0for i in range(len(nums)):if nums[i] == 0:nums[i], nums[start] = nums[start], nums[i]start += 1# 再将1进行交换放在0后面for i in range(len(nums)):if nums[i] == 1:nums[i], nums[start] = nums[start], nums[i]start += 1print('==nums:', nums)return numsnums = [2, 0, 2, 1, 1, 0]
sol = Solution()
sol.sortColors(nums)

思路2:计数排序:对每种颜色进行计数,然后根据个数去修改nums数组
class Solution:def sortColors(self, nums):print('==nums:', nums)count = [0] * 3for i in range(len(nums)):if nums[i] == 0:count[0] += 1elif nums[i] == 1:count[1] += 1else:count[-1] += 1print('==count:', count)p = 0for i in range(len(count)):num = count[i]while num>0:nums[p] = inum-=1p += 1print('==nums:', nums)return nums
nums = [2, 0, 2, 1, 1, 0]
sol = Solution()
sol.sortColors(nums)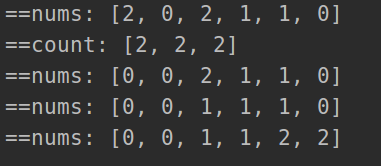
30-1.最小覆盖子串

思路:滑动窗口 左指针先不动,右指针遍历找到所有t中出现的字符,左指针在移动缩小范围即可
class Solution:def minWindow(self, s, t):dict_ = {}for i in t:dict_[i] = dict_.get(i, 0)+1print('dict_:', dict_)n = len(s)left, right = 0,0remain=0res = ''minlen = float('inf')while right<n:#向右边拓展if s[right] in dict_:if dict_[s[right]]>0:#大于0这个时候加才有效否则是重复字符remain+=1dict_[s[right]]-=1while remain==len(t):#left 要拓展了 也就是左边要压缩if (right - left)<minlen:minlen = right-leftres = s[left:right+1]print('==res:', res)left+=1if s[left-1] in dict_:#注意这里left已经加1了 要用前一个字符也就是s[left-1]dict_[s[left - 1]] += 1if dict_[s[left-1]]>0:#大于0这个时候减去才有效否则是重复字符remain -= 1right += 1#放后面进行向右拓展print('==res:', res)return ress = "ADOBECODEBANC"
t = "ABC"
# s = "bba"
# t = "ab"
sol = Solution()
sol.minWindow(s, t)
30-2.字符串的排列

思路:滑动窗口,先向右扩张,在左边收缩 python代码
class Solution:def checkInclusion(self, s1, s2):dict_={}for i in s1:dict_[i] = dict_.get(i,0)+1print('==dict_:',dict_)left,right =0,0length = 0minlen = float('inf')res = ''while right<len(s2):# 向右拓展if s2[right] in dict_:if dict_[s2[right]]>0:#注意要进行判断避免重复字符length+=1dict_[s2[right]]-=1while length==len(s1):#包含了子串啦 这个时候左边要压缩if right-left+1==len(s1):#找最短的return Trueleft+=1if s2[left-1] in dict_:#注意left+1啦 所以要用left-1的字符判断是否出现在dict_中dict_[s2[left - 1]] += 1if dict_[s2[left-1]]>0:#避免重复字符造成的减法length-=1right+=1return Falses1 = "ab"
s2 = "eidbaooo"
sol = Solution()
res= sol.checkInclusion(s1, s2)
print(res)
c++代码:
#include <string>
#include <iostream>
#include <vector>
#include <list>
#include <map>using namespace std;class Solution {
public:bool checkInclusion(string s1, string s2) {map<char,int> dict_;for (int k=0;k<s1.size();k++){dict_[s1[k]]++;}// map <char,int>::iterator itor = dict_.begin(); // //debug// for(;itor!=dict_.end();itor++)// {// cout<<itor->first<<" "<<itor->second<<endl;// } int right=0;int left=0;int remain_legth =0;while (right<s2.size()){ if(dict_[s2[right]]>0){remain_legth+=1;}dict_[s2[right]]-=1; cout<<"remain_legth:"<<remain_legth<<endl;while(remain_legth==s1.size()){ cout<<"==right:"<<right<<endl;cout<<"==left:"<<left<<endl;if(right-left+1==s1.size()){return true;} left+=1;dict_[s2[left-1]]+=1; if (dict_[s2[left-1]]>0){remain_legth-=1;}}right+=1;}return false;
}
};int main()
{ // string s1 = "ab";// string s2 = "eidbaooo";string s1 = "ab";string s2 = "eidboaoo";Solution sol;bool res = sol.checkInclusion(s1, s2);cout<<"res:"<<res<<endl;return 0;
}30-3.找到字符串中所有字母异位词

思路1.hash 超时了
#超时间复杂度
class Solution:def findAnagrams(self, s, p):dict_ = {}for str_ in p:dict_[str_] = dict_.get(str_, 0)+1print('==dict_:', dict_)m = len(s)n = len(p)res = []for i in range(m-n+1):print('==s[i:n]:', s[i:i+n])new_str = s[i:i + n]new_dict = {}for str_ in new_str:if str_ not in dict_:breaknew_dict[str_] = new_dict.get(str_, 0)+1if dict_ == new_dict:res.append(i)return ress = "cbaebabacd"
p = "abc"
sol = Solution()
res = sol.findAnagrams(s, p)
print('==res:', res)
思路2.滑动窗口
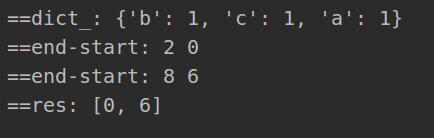
class Solution:def findAnagrams(self, s, p):dict_ = {}for i in p:dict_[i] =dict_.get(i,0)+1print(dict_)length = 0left,right = 0,0res = []while right<len(s):#往右拓展if s[right] in dict_:if dict_[s[right]]>0:#注意判断避免重复字符进行多次计数length+=1dict_[s[right]]-=1while length==len(p):#往左压缩if length==right-left+1:res.append(left)left+=1#往左压缩#注意left进行了加1 要用left-1去修正dictif s[left-1] in dict_:dict_[s[left-1]]+=1if dict_[s[left-1]]>0:#注意判断避免重复字符进行多次计数length-=1right+=1print(res)return ress= "cbaebabacd"
p = "abc"
sol = Solution()
sol.findAnagrams(s, p)
30-4.无重复字符的最长子串

思路:滑动窗口,先往右拓展字典进行加1,发现大于1的在往左压缩 python代码
class Solution:def lengthOfLongestSubstring(self, s):n = len(s)left = 0right = 0dict_= {}res = 0while right<n:#往右拓展dict_[s[right]] = dict_.get(s[right], 0)+1#出现就加1while dict_[s[right]]>1:#解决这种两个连续ww的问题"pwwkew" 再次出现往左压缩dict_[s[left]]-=1left+=1res = max(res, right-left+1)right+=1return res# s = "abcabcbb"
# s = "dvdf"
s = "pwwkew"
sol = Solution()
sol.lengthOfLongestSubstring(s)c++代码:
#include <string>
#include <iostream>
#include <vector>
#include <list>
#include <map>
#include <typeinfo>using namespace std;class Solution {
public:int lengthOfLongestSubstring(string s) {int left = 0;int right = 0;int res=0;map <char, int> dict_;while (right<s.size()){ dict_[s[right]]+=1;while (dict_[s[right]]>1){ dict_[s[left]]-=1;left+=1;} // cout<<"dict_[s[right]]:"<<dict_[s[right]]<<endl; // cout<<"right:"<<right<<endl;// cout<<"left:"<<left<<endl;res = max(res, right-left+1);right+=1;}return res; }
};int main()
{ string s = "abcabc";// Solution sol;// int res;// res= sol.lengthOfLongestSubstring(s);int res;Solution *sol = new Solution();res = sol->lengthOfLongestSubstring(s);delete sol;sol = NULL; cout<<"res:"<<res<<endl;return 0;
}31.单词搜索

思路:与岛屿,水塘类似,只不过添加一个回溯的过程,直接修改board即可,回溯出来还原即可
class Solution:def help(self, i, j, h, w, index):if i<0 or j<0 or i>=h or j>=w or self.word[index] != self.board[i][j]:return Falseif index == len(self.word) - 1:return Trueself.board[i][j] = ''#说明board和word找到相同的 因为不能重复 修改一下boradfor direction in self.directions:new_i, new_j = direction[0] + i, direction[1] + jif self.help(new_i, new_j, h, w, index + 1):return Trueself.board[i][j] = self.word[index]#回溯出去需要还原return Falsedef exist(self, board: List[List[str]], word: str) -> bool:self.board = boardself.word = wordself.directions = [(-1, 0), (0, -1), (1, 0), (0, 1)]h = len(board)w = len(board[0])for i in range(h):for j in range(w):if self.help(i, j, h, w, 0):return Truereturn Falsec++实现:
class Solution {
public:int h, w;vector<vector<char>> board;string word;int directions[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};bool help(int i, int j, int index){if(i < 0 || j < 0 || i > h - 1 || j > w - 1 || this->word[index] != this->board[i][j]){return false;}if(index == this->word.size() - 1){return true;}this->board[i][j] = '#';for(int k = 0; k < sizeof(directions) / sizeof(directions[0]); k++){if(help(directions[k][0] + i, directions[k][1] + j, index + 1)){return true;}}this->board[i][j] = this->word[index];return false;}bool exist(vector<vector<char>>& board, string word) {this->h = board.size();this->w = board[0].size();this->board = board;this->word = word;for(int i = 0; i < this->h; i++){for(int j = 0; j < this->w; j++){if(help(i, j, 0)){return true;}}}return false;}
};
32.柱状图中最大的矩形

思路1:暴力枚举,直接向左右扩撒直到找到小于heights[i]的点
超时:

class Solution:def largestRectangleArea(self, heights):res = 0for i in range(len(heights)):# print('==i:', i)left_i = iright_i = i# print(stack)while left_i >= 0 and heights[left_i] >= heights[i]:left_i-=1while right_i<len(heights) and heights[right_i] >= heights[i]:right_i+=1# print('==left_i,right_i:', left_i,right_i)res = max(res, (right_i - left_i - 1)*heights[i])return res
heights = [2,1,5,6,2,3]
# heights = [0,9]
# heights = [2,0,2]
# heights = [4,2,0,3,2,4,3,4]
sol = Solution()
sol.largestRectangleArea(heights)思路2:单调递增栈

#单调递增栈 将依次增加的值放入栈中,出现小于栈的值则进行出栈计算面积
class Solution:def largestRectangleArea(self, heights):stack = []heights = [0] + heights + [0]res = 0for i in range(len(heights)):while stack and heights[stack[-1]] > heights[i]:# print('heights', heights)print('===i:', i)print('==stack:', stack)tmp = stack.pop()print('==tmp:', tmp)width = (i - stack[-1] - 1)res = max(res, width * heights[tmp])print('==res:', res)stack.append(i)return res
heights = [2,1,5,6,2,3]
# heights = [0,9]
# heights = [2,0,2]
# heights = [4,2,0,3,2,4,3,4]
sol = Solution()
sol.largestRectangleArea(heights)
c++实现:
class Solution {
public:int largestRectangleArea(vector<int>& heights) {heights.push_back(0);heights.insert(heights.begin(), 0);vector<int> stack;int max_area = 0;for(int i = 0; i < heights.size(); i++){while(!stack.empty() && heights[i] < heights[stack.back()]){int index = stack.back();stack.pop_back();int width = i - 1 - stack.back();int height = heights[index];max_area = max(max_area, width * height);}stack.push_back(i);}return max_area;}
};33.最大矩形
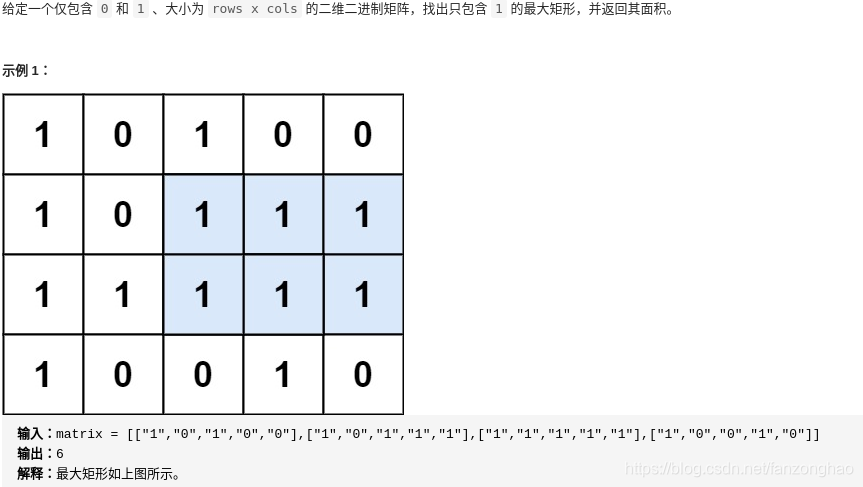
思路1:动态规划 获取最长宽度
if 0, dp[i][j]=1
if 1, dp[i][j]=dp[i][j-1]+1
找到右下角在往上去找到高度和最小宽度即可求矩形面积
import numpy as np
class Solution:def maximalRectangle(self, matrix):print('==np.array(matrix):\n', np.array(matrix))h = len(matrix)if h==0:return 0w= len(matrix[0])dp = [[0 for i in range(w)] for i in range(h)]# print('==np.array(dp):', np.array(dp))max_area = 0for i in range(h):for j in range(w):if j>0 and matrix[i][j]=='1':dp[i][j] = dp[i][j-1]+1elif j == 0:dp[i][j] = int(matrix[i][j])else:passwidth = dp[i][j]for k in range(i,-1,-1):height = i-k+1width = min(width, dp[k][j])max_area = max(max_area, height*width)print('==np.array(dp):\n', np.array(dp))print('===max_area:', max_area)return max_area# matrix = [["1","0","1","0","0"],
# ["1","0","1","1","1"],
# ["1","1","1","1","1"],
# ["1","0","0","1","0"]]matrix = [["0", "0", "0"],["1", "1", "1"]]
sol = Solution()
sol.maximalRectangle(matrix)
思路2,采用单调递增栈,也就是139.柱状图中最大的矩形,那么构造出高度列表即可以求出最大面积,如下图所示,橙色就是每一行需要抓换的高度列表
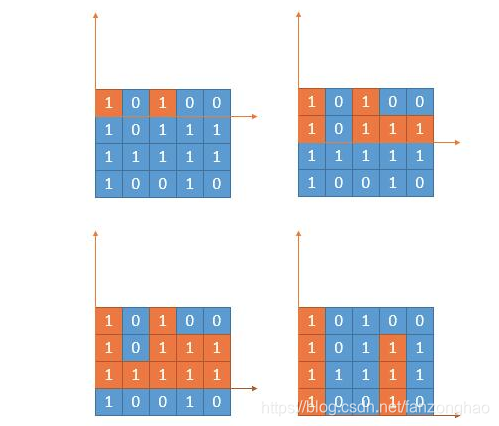
import numpy as np#
class Solution:def largestRectangleArea(self, heights):stack = []heights = [0] + heights + [0]res = 0for i in range(len(heights)):while stack and heights[stack[-1]] > heights[i]:index = stack.pop()width = i - stack[-1] - 1res = max(res, width * heights[index])stack.append(i)return resdef maximalRectangle(self, matrix):if not matrix: return 0print('==np.array(matrix):\n', np.array(matrix))h = len(matrix)w = len(matrix[0])heights = [0] * wmax_area = 0for i in range(h):for j in range(w):if matrix[i][j] == '1':heights[j] += 1else:heights[j] = 0print('==heights:', heights)max_area = max(max_area, self.largestRectangleArea(heights))print('==max_area:', max_area)return max_area# matrix = [["1", "0", "1", "0", "0"],
# ["1", "0", "1", "1", "1"],
# ["1", "1", "1", "1", "1"], ["1", "0", "0", "1", "0"]]
# matrix = [["1"]]
# matrix = [["1", "1"]]
# matrix = [["0", "0", "0"],
# ["1", "1", "1"]]
matrix = [["0","1"],["1","0"]]
sol = Solution()
sol.maximalRectangle(matrix)34.中序遍历

思路1:递归法
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def helper(self, node):if node is not None:self.helper(node.left)self.res.append(node.val)self.helper(node.right)def inorderTraversal(self, root: TreeNode) -> List[int]:self.res = []self.helper(root)return self.res

c++实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int>res;void help(TreeNode* node){if(node){help(node->left);res.push_back(node->val);help(node->right);}}vector<int> inorderTraversal(TreeNode* root) {help(root);return res;}
};思路2.栈(迭代法)
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def inorderTraversal(self, root):""":type root: TreeNode:rtype: List[int]"""stack = []node = rootoutput = []if root == None: return outputwhile node or stack: # 如果node和aStack都是空的,说明全查完了。while node: # 如果node是空的,说明左边没子节点了。stack.append(node)node = node.leftnode = stack.pop() # 左边没子节点了就输出栈顶的节点值,然后从它右边的子节点继续。output.append(node.val)node = node.rightreturn output35-1.不同的二叉搜索树

思路:卡塔兰数
将 1⋯(i−1) 序列作为左子树,将 (i+1)⋯n 序列作为右子树。接着我们可以按照同样的方式递归构建左子树和右子树。
在上述构建的过程中,由于根的值不同,因此我们能保证每棵二叉搜索树是唯一的.也就得到卡塔兰数

class Solution(object):def numTrees(self, n):""":type n: int:rtype: int"""#状态方程 和G(j-1) * G(n-j)dp = [0]*(n+1)#0 1树都为1dp[0], dp[1] = 1, 1for i in range(2,n+1):for j in range(1,i+1):dp[i] += dp[j-1]*dp[i-j]# print('==dp:', dp)return dp[-1]c++实现:
class Solution {
public:int numTrees(int n) {vector<int> res(n+1,0); res[0] = 1;res[1] = 1;for (int i=2;i<n+1;i++){for (int j=1;j<i+1;j++){res[i] += res[j-1] * res[i-j];}}return res[n];}
};35-2.不同的二叉搜索树 II

思路:

# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution(object):def generateTrees(self, n):""":type n: int:rtype: List[TreeNode]"""if n==0:return []def build_tree(left,right):if left > right:#递归终止条件 如果左边计数大于右边 说明要返回空值return [None]all_trees = []for i in range(left, right+1):left_trees = build_tree(left, i-1)right_trees = build_tree(i+1, right)for l in left_trees:#遍历可能的左子树for r in right_trees:#遍历可能的右子树cur_tree = TreeNode(i)#根节点cur_tree.left= lcur_tree.right = rall_trees.append(cur_tree)return all_treesres = build_tree(1,n)return res36.验证二叉搜索树

思路1:递归处理右子树节点和 左子树节点的值和上下界限的大小
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution(object):def isValidBST(self, root):""":type root: TreeNode:rtype: bool"""def helper(node, lower=float('-inf'), upper=float('inf')):if node is None:#递归终止条件 节点为Nonereturn Trueval = node.val#获取节点值#如果节点值大于上界或者小于下界 ,返回falseif val >= upper or val <= lower :return False#递归右子树 对于右子树 具备下界if not helper(node.right, val, upper):return False#递归左子树 对于左子树 具备上界if not helper(node.left, lower, val):return Falsereturn Truereturn helper(root)c++实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool help(TreeNode* node, long long lower,long long upper){if(node == nullptr){return true;}if(node->val <= lower || node->val >= upper){return false;}if(!help(node->right, node->val, upper)){return false;}if(!help(node->left, lower, node->val)){return false;}return true;}bool isValidBST(TreeNode* root) {if(root == nullptr){return true;}return help(root, LONG_MIN, LONG_MAX);}
};
思路2 :利用中序遍历的特点,遍历左子树和根节点,如果值不满足二叉搜索数特点就返回false.
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution(object):def isValidBST(self, root):stack = []node = rootinorder_value = float('-inf')while stack or node:#出栈终止条件while node:#进栈stack.append(node)node = node.leftnode = stack.pop()#左节点# 如果中序遍历得到的节点的值小于等于前一个 inorder_value,说明不是二叉搜索树if node.val <=inorder_value:return Falseinorder_value = node.val node=node.rightreturn True
思路3:递归实现中序遍历 左 跟 右 也就是遍历的后一个节点值要大于上一个 否则不满足二叉搜索树特点
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
#中序遍历 左跟右
class Solution:def __init__(self):self.pre = float('-inf')def isValidBST(self, root: TreeNode) -> bool:if root is None:return Trueif not self.isValidBST(root.left):#先访问左子树return Falseif root.val<=self.pre:#在访问当前节点return False;print('==before self.pre:',self.pre)self.pre = root.valprint('==after self.pre:',self.pre)return self.isValidBST(root.right)#在访问右子树
37.对称二叉树

1.解法1 bfs 对每个节点的左子树和右子树进行判断相等
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def isSymmetric(self, root: TreeNode) -> bool:def check(t1,t2):if t1==None and t2==None:return Trueif t1==None or t2==None:return Falseif (t1.val != t2.val):return Falsereturn check(t1.left,t2.right) and check(t1.right,t2.left)return check(root,root)
c++实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:bool dfs(TreeNode* t1, TreeNode* t2){if(t1==nullptr && t2==nullptr){return true;}if(t1==nullptr || t2==nullptr){return false;}return dfs(t1->left,t2->right) && dfs(t1->right,t2->left);}bool isSymmetric(TreeNode* root) {return dfs(root, root);}
};2.解法2 dfs ,首先对根节点左子树进行前序遍历并存储值,对根节点右子树的右分支进行遍历在对左分支进行遍历并存储值,最后比较两个列表的值。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def isSymmetric(self, root: TreeNode) -> bool:if root==None:return Truedef leftsearch(t1, left):if t1==None:left.append(None)else:left.append(t1.val)leftsearch(t1.left,left)leftsearch(t1.right,left)def rightsearch(t2, right):if t2==None:right.append(None)else:right.append(t2.val)rightsearch(t2.right,right)rightsearch(t2.left,right)left = []right = []leftsearch(root.left, left)rightsearch(root.right, right)if left==right:return Trueelse:return False38. 二叉树的层序遍历

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def levelOrder(self, root: TreeNode) -> List[List[int]]:res = []if root is None:return res quene = [root]while quene:temp = []for i in range(len(quene)):node = quene.pop(0)temp.append(node.val)if node.left:quene.append(node.left)if node.right:quene.append(node.right)res.append(temp)return res39.二叉树的最大深度

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def maxDepth(self, root: TreeNode) -> int:if root is None:return 0return max(self.maxDepth(root.left),self.maxDepth(root.right))+140-1.从前序与中序遍历序列构造二叉树

思路:
终止条件:前序或中序数组为空.
根据前序数组第一个元素,拼出根节点,再将前序数组和中序数组分成两半,递归的处理前序数组左边和中序数组左边,递归的处理前序数组右边和中序数组右边。

# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode: # 递归终止条件 前序遍历节点数或中序遍历节点数为0if len(preorder)==0 or len(inorder)==0:return Noneroot = TreeNode(preorder[0])#根据前序遍历特点创建根节点#再根据中序遍历特点用根节点找出左右子树的分界点mid_index = inorder.index(preorder[0])#再利用中序遍历和前序遍历的左子树节点个数相等特点 构造根节点左子树root.left = self.buildTree(preorder[1:mid_index+1],inorder[:mid_index])#再利用中序遍历和前序遍历的右子树节点个数相等特点 构造根节点右子树root.right = self.buildTree(preorder[mid_index+1:],inorder[mid_index+1:])return rootc++实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.empty() || preorder.empty()) {return nullptr;}TreeNode* root = new TreeNode(preorder[0]);int root_value = preorder[0];int middle = 0;for (int i=0;i<inorder.size();i++){if(inorder[i]==root_value){middle = i;break;}}vector<int> leftInorder(inorder.begin(), inorder.begin() + middle);vector<int> rightInorder(inorder.begin() + middle + 1, inorder.end());vector<int> leftPreorder(preorder.begin()+1, preorder.begin() + middle+1);vector<int> rightPreorder(preorder.begin() + middle + 1, preorder.end());root->left = buildTree(leftPreorder,leftInorder);root->right = buildTree(rightPreorder,rightInorder);return root;}
};40-2.从中序与后序遍历序列构造二叉树

思路:和上一题类似
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = Noneclass Solution:def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:#递归终止条件if len(inorder)==0 or len(postorder)==0:return None#创建根节点root = TreeNode(postorder[-1])#根据中序遍历获取分离点mid_index = inorder.index(postorder[-1])# print('==mid_index:',mid_index)#获取左子树root.left = self.buildTree(inorder[:mid_index],postorder[:mid_index])#获取右子树root.right = self.buildTree(inorder[mid_index+1:],postorder[mid_index:-1])return rootc++实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {if(inorder.empty() || postorder.empty()){return nullptr;}TreeNode* root = new TreeNode(postorder[postorder.size()-1]);int root_value = postorder[postorder.size()-1];int middle = 0;for (int i=0; i<inorder.size(); i++){if(inorder[i] == root_value){middle = i;break;}}// cout<<"===middle:"<<middle<<endl;vector<int> left_inorder(inorder.begin(), inorder.begin() + middle);vector<int> right_inorder(inorder.begin() + middle + 1, inorder.end());vector<int> left_postorder(postorder.begin(), postorder.begin() + middle);vector<int> right_postorder(postorder.begin() + middle, postorder.end() - 1);root->left = buildTree(left_inorder, left_postorder);root->right = buildTree(right_inorder, right_postorder);return root;}
};由上面两题可知对于前序遍历:跟左右,中序遍历:左跟右,后序遍历左右跟;
采前序遍历和中序遍历,中序遍历和后序遍历都能通过根节点分离出左右,而前序遍历和后序遍历就不能,故而后者无法恢复出二叉树.
41.二叉树展开为链表

思路:可看出是根据前序遍历的节点统统放在右子树上
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def help(self, node):if node is not None:self.res.append(node)self.help(node.left)self.help(node.right)def flatten(self, root: TreeNode) -> None:"""Do not return anything, modify root in-place instead."""self.res = []self.help(root)# print(self.res)length = len(self.res)for i in range(1,length):pre,cur = self.res[i-1],self.res[i]pre.left = Nonepre.right = curreturn rootc++实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<TreeNode* >res;void help(TreeNode* node){if(node){res.push_back(node);help(node->left);help(node->right);}}void flatten(TreeNode* root) {help(root);for(int i=1;i<res.size();i++){TreeNode* pre = res[i-1];TreeNode* cur = res[i];pre->left = nullptr;pre->right = cur;}// return root;}
};42-1.买卖股票的最佳时机

思路1:动态规划用来存储最小和最大值之间差距
状态转移方程 不卖或者卖 opt[i] = max(opt[i-1], prices[i]-min_price)
class Solution:def maxProfit(self, prices: List[int]) -> int:if len(prices) <= 1:return 0opt = len(prices)*[0]min_price = prices[0]for i in range(1, len(prices)):if prices[i]<min_price:min_price = prices[i]opt[i] = max(opt[i-1], prices[i]-min_price)# print('opt:', opt)return opt[-1]思路2:就是存储最小最大值的差值即可
class Solution:def maxProfit(self, prices: List[int]) -> int:#dp[i] = max(dp[i-1],prices[i] - minprice)if len(prices)<=0:return 0# dp = len(prices)*[0]minprice = prices[0]res = 0for i in range(1,len(prices)):if prices[i]<minprice:minprice = prices[i]# dp[i] = max(dp[i-1], prices[i]-minprice)res = max(res, prices[i]-minprice)# print(dp)return res思路3:利用单调递增栈,找到元素小于栈顶的,则更新此时的最大利润, 对于一直递增的要特意在prices增加一个负数 作为递增拐点
class Solution:def maxProfit(self, prices):if len(prices)<=1:return 0stack = []res = 0prices.append(-1)# print('==prices:', prices)for i in range(len(prices)):while stack and prices[i] <= prices[stack[-1]]:print('==stack:', stack)res = max(res, prices[stack[-1]]-prices[stack[0]])print('==res:', res)stack.pop()stack.append(i)# print('==stack:', stack)return resprices = [7,1,5,3,6,4]
# prices = [1,2]
sol = Solution()
sol.maxProfit(prices)
class Solution {
public:int maxProfit(vector<int>& prices) {if(prices.size() <= 1){return 0;}vector<int> stack;int max_profit = 0;prices.push_back(-1);for(int i = 0; i < prices.size(); i++){while(!stack.empty() && prices[i] < prices[stack[stack.size() - 1]]){ max_profit = max(max_profit, prices[stack[stack.size() - 1]] - prices[stack[0]]);stack.pop_back();}stack.push_back(i);}return max_profit; }
};42-2.买卖股票的最佳时机 II

思路1:与上一题差异在于对次数没有限制,所以采用贪心算法,一直累加
class Solution:def maxProfit(self, prices):if len(prices)<=1:return 0# opt = len(prices)*[0]res = 0for i in range(1,len(prices)):if prices[i]>prices[i-1]:res+=prices[i]- prices[i-1]print('===res:', res)return resprices = [7,1,5,3,6,4]
sol = Solution()
sol.maxProfit(prices)class Solution:def maxProfit(self, prices: List[int]) -> int:if len(prices)<=1:return 0# opt = len(prices)*[0]res = 0for i in range(1,len(prices)):if prices[i]>prices[i-1]:res+=prices[i]- prices[i-1]# print('===res:', res)return res思路2:dp解法
dp存储有无的利润
今天无股票:1.昨天就没有,今天不操作; 2.昨天有,今天卖了
今天有股票:1.昨天有,今天不操作; 2.昨天无,今天买
1代表有 0代表无
dp[i][0] =max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] =max(dp[i-1][1],dp[i-1][0]-prices[i])
class Solution:def maxProfit(self, prices):# res = 0# for i in range(1, len(prices)):# if prices[i]>prices[i-1]:# res +=prices[i] - prices[i-1]# return resn = len(prices)dp = [[0 for i in range(2)] for i in range(n)]print('==dp:', dp)dp[0][1] = -prices[0]for i in range(1, n):dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i])print('==dp:', dp)return dp[-1][0]#返回没有的最大利润
prices = [7, 1, 5, 3, 6, 4]
sol = Solution()
sol.maxProfit(prices)
class Solution {
public:int maxProfit(vector<int>& prices) {int n = prices.size();if(n <= 1){return 0;}vector<vector<int>> dp(n, vector<int>(2, 0)); //dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]) //dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])//dp[0][1] = -prices[0]dp[0][1] = -prices[0];for(int i = 1; i < n; i++){dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]);}return max(dp[n-1][0], dp[n-1][1]);}
};42-3.买卖股票的最佳时机含手续费

dp解法: dp存储有无的利润
今天无股票:1.昨天就没有,今天不操作; 2.昨天有,今天卖了 在减去费用
今天有股票:1.昨天有,今天不操作; 2.昨天无,今天买
1代表有 0代表无
dp[i][0] =max(dp[i-1][0],dp[i-1][1]+prices[i]-fee)
dp[i][1] =max(dp[i-1][1],dp[i-1][0]-prices[i])
class Solution:def maxProfit(self, prices, fee):dp = [[0 for i in range(2)] for i in range(len(prices))]dp[0][1] = -prices[0]for i in range(1, len(prices)):dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i] - fee)dp[i][1] = max(dp[i-1][1], dp[i-1][0]-prices[i])print('==dp:', dp)return dp[-1][0]prices = [1, 3, 2, 8, 4, 9]
fee = 2
sol = Solution()
sol.maxProfit(prices, fee)
42-4.最佳买卖股票时机含冷冻期

思路:和上一题不用的是增加了冷冻期,故状态方程dp[i]不在由dp[i-1]来,而是dp[i-2]来的
今天无股票:1.昨天就没有,今天不操作; 2.昨天有,今天卖了
今天有股票:1.昨天有,今天不操作; 2.昨天是冷冻期,前天卖出,今天买
1代表有 0代表无
dp[i][0] =max(dp[i-1][0],dp[i-1][1]+prices[i])
dp[i][1] =max(dp[i-1][1],dp[i-2][0]-prices[i])
class Solution:def maxProfit(self, prices):if len(prices) <= 1:return 0dp = [[0 for i in range(2)] for i in range(len(prices))]print('==dp:', dp)dp[0][1] = -prices[0]dp[1][0] = max(dp[1 - 1][0], dp[1 - 1][1] + prices[1])dp[1][1] = max(dp[1-1][1], -prices[1])for i in range(2, len(prices)):dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i])dp[i][1] = max(dp[i - 1][1], dp[i - 2][0] - prices[i])print('==dp:', dp)return dp[-1][0]#返回没有的最大利润
prices = [1, 2, 3, 0, 2]
sol = Solution()
sol.maxProfit(prices)
42-5.买卖股票的最佳时机 III

#dp[i][j][0] 不持有利润
#dp[i][j][1] 持有的利润
# i代表天数,j代表买入次数
#昨天可能持有也可能没有持有,昨天持有今天卖了dp[i-1][j][1]+prices[i],昨天没有dp[i-1][j][0]
#dp[i][j][0] = max(dp[i-1][j][0],dp[i-1][j][1]+prices[i])
#昨天持有也可能没有持有,昨天持有dp[i-1][j][1],昨天没有持有dp[i-1][j-1][0]-prices[i]
#dp[i][j][1] = max(dp[i-1][j][1], dp[i-1][j-1][0]-prices[i])
class Solution:def maxProfit(self, prices):#k代表交易次数,本题为0,1,2n = len(prices)k = 2dp = [[[0, 0] for i in range(k+1)] for _ in range(n)]for i in range(n):#边界条件1:第i天不买入是否持有的利润dp[i][0][0] = 0dp[i][0][1] = float('-inf')#用负无穷代表不可能# print(dp)for j in range(1, k+1):#边界条件2:第0天买入是否持有的利润dp[0][j][0] = 0dp[0][j][1] = -prices[0]for i in range(1, n):for j in range(1,k+1):dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i])dp[i][j][1] = max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i])return dp[-1][-1][0]prices = [3,3,5,0,0,3,1,4]
sol = Solution()
sol.maxProfit(prices)
43.二叉树中的最大路径和
递归 主要是要找准递归终止条件和递归出口,终止条件就是节点为none自然返回值为0, 递归出口就是节点本身值+max(左节点增益值,右节点增益值)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def helper(self, node):if node is None:return 0left_gain = self.helper(node.left)right_gain = self.helper(node.right)self.max_gain = max(self.max_gain,left_gain+right_gain+node.val)return max(node.val+left_gain,node.val+right_gain,0)def maxPathSum(self, root: TreeNode) -> int:self.max_gain = float('-inf')self.helper(root)return self.max_gainc++实现:
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int max_value=INT_MIN;int helper(TreeNode *node){if(!node){return 0;}int left_gain = helper(node->left);int right_gain = helper(node->right);max_value = max(max_value, node->val+left_gain+right_gain);return max(max(node->val+left_gain,0),node->val+right_gain);}int maxPathSum(TreeNode* root) {helper(root);return max_value;}
};44.最长连续序列

class Solution:def longestConsecutive(self, nums):longest_length = 0num_set = set(nums)#set 比list 快几十倍print('==num_set:', num_set)temp = 1for num in num_set:if num - 1 in num_set:#如果有小于的就跳过continueelse:while num+1 in num_set:#如果有大于的就一直不停更新+1 寻找长度temp += 1num += 1longest_length = max(longest_length, temp)temp = 1#寻找完结束以后 在初始化为1print('==longest_length:', longest_length)return longest_lengthnums = [100,4,200,1,3,2,2]
sol = Solution()
sol.longestConsecutive(nums)
45-1.只出现一次的数字
1,给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。

思路:利用异或,相同为0,不同为1
#方法1
a=[4,1,2,2,1]
b=set(a)
print(b)
print(2*sum(b)-sum(a))#方法2:
a=[4,1,1]
res=0
for i in a:res^=i
print('res=',res)#方法3:
a=[4,1,2,1,2]
from functools import reduce
b=reduce(lambda x,y:x^y,a)
print('b=',b)45-2.只出现一次的数字 II
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
思路:0与任何数异或为该数,两个相同的数异或为0,需要两个位运算符来存储单次和三次出现的值
class Solution:def singleNumber(self, nums: List[int]) -> int:# return (3 * sum(set(nums)) - sum(nums)) // 2seen_once = seen_twice = 0for num in nums:seen_once = ~seen_twice & (seen_once ^ num)seen_twice = ~seen_once & (seen_twice ^ num)return seen_once46-1. 单词拆分

思路1:动态规划
#动态规划 dp[i]表示 s 的前 i 位是否可以用 wordDict 中的单词表示,
#
class Solution:def wordBreak(self, s, wordDict):n = len(s)dp = [False] * (n + 1)dp[0] = Truefor i in range(n):for j in range(i+1, n+1):if dp[i] and (s[i:j] in wordDict):dp[j] = Trueprint('==dp:', dp)return dp[-1]
s = "leetcode"
wordDict = ["leet", "code"]
sol = Solution()
res= sol.wordBreak(s, wordDict)
print('==res:', res)
c++实现:
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {int n = s.size();unordered_set<string> wordDictSet;for (auto word: wordDict) {wordDictSet.insert(word);} vector<bool> dp(n+1, false);dp[0] = true;for(int i = 0; i < n; i++){for(int j = i+1; j < n+1; j++){ if(dp[i] && wordDictSet.find(s.substr(i, j - i)) != wordDictSet.end()) {// cout<<"s.substr(i, j - i):"<<s.substr(i, j - i)<<endl;dp[j] = true;}}}return dp[n];}
};思路2:回溯加缓存
#递归 lru_cache用于缓存 将数据缓存下来 加快后续的数据获取 相同参数调用时直接返回上一次的结果
import functools
class Solution:@functools.lru_cache()def helper(self, s):if len(s) == 0:return Trueres = Falsefor i in range(1, len(s)+1):if s[:i] in self.wordDict:res = self.helper(s[i:]) or resreturn resdef wordBreak(self, s, wordDict):self.wordDict = wordDictreturn self.helper(s)
s = "leetcode"
wordDict = ["leet", "code"]
# s = "aaaaaaa"
# wordDict = ["aaaa", "aaa"]
# s= "aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaab"
# wordDict = ["a","aa","aaa","aaaa","aaaaa","aaaaaa","aaaaaaa","aaaaaaaa","aaaaaaaaa","aaaaaaaaaa"]
sol = Solution()
res= sol.wordBreak(s, wordDict)
print('==res:', res)
46-2.单词拆分 II

思路:递归
class Solution:def helper(self, s, wordDict, memo):if s in memo:#递归终止条件return memo[s]if s=='':#递归终止条件return []res = []for word in wordDict:if not s.startswith(word):continueif len(word)==len(s):#匹配上刚好相等res.append(word)else:#匹配上 但是字符还没到最后rest = self.helper(s[len(word):], wordDict, memo)for tmp in rest:tmp = word+ " "+ tmpres.append(tmp)print('==res:', res)print('==memo:', memo)memo[s] = resreturn resdef wordBreak(self, s, wordDict):if s=='':return []return self.helper(s, wordDict, memo={})
s = "catsanddog"
wordDict = ["and", "cat", "cats", "sand", "dog"]
# s = "cat"
# wordDict = ["cat"]
sol = Solution()
res = sol.wordBreak(s, wordDict)
print(res)
47-1.环形链表

# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = Noneclass Solution:def hasCycle(self, head: ListNode) -> bool:#快慢指针 人追人slow,fast = head,headwhile fast:if fast and fast.next:slow = slow.nextfast=fast.next.nextelse:return Falseif slow==fast:return Truereturn Falsec++实现:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:bool hasCycle(ListNode *head) {ListNode* slow = head;ListNode* fast = head;while(fast){if(fast && fast->next){slow = slow->next;fast = fast->next->next;}else{return false;}if(slow==fast){return true;}}return false;}
};47-2.给定一个有环链表,实现一个算法返回环路的开头节点。

假设有两个指针,分别为快慢指针fast和slow, 快指针每次走两步,慢指针每次前进一步,如果有环则两个指针必定相遇;
反证法:假设快指针真的 越过 了慢指针,且快指针处于位置 i+1,而慢指针处于位置 i,那么在前一步,快指针处于位置 i-1,慢指针也处于位置 i-1,它们相遇了。
A:链表起点
B:环起点
C:相遇点
X:环起点到相遇点距离
Y:链表起点到环起点距离
R:环的长度
S:第一次相遇时走过的路程
1.慢指针slow第一次相遇走过的路程 S1 = Y + X;(11)
快指针fast第一次相遇走过的路程 S2=2S1 = Y + X + NR;(2)
说明:快指针的速度是慢指针的两倍,相同时间内路程应该是慢指针的两倍,Y + X + NR是因为快指针可能经过N圈后两者才相遇;
把(1)式代入(2)式得:Y = NR -X;
2..在将慢指针回到A点,满指针和快指针同时走,在B点相遇,此处就是环节点.
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = Noneclass Solution:def detectCycle(self, head: ListNode) -> ListNode:slow = headfast = head;while fast:if fast and fast.next:slow = slow.nextfast = fast.next.nextelse:return Noneif slow==fast:breakif fast ==None or fast.next==None:return Noneslow= headwhile slow!=fast:slow = slow.nextfast = fast.nextreturn slowc++实现:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* slow = head;ListNode* fast = head;while(fast){if(fast && fast->next){slow = slow->next;fast = fast->next->next;}else{return NULL;}if(slow==fast){break;}}if(!fast || !fast->next){return NULL;}slow = head;while(slow!=fast){slow = slow->next;fast = fast->next;}return slow;}
};47-3.链表相交

如这题应该是比较明显的双指针题,要是能实现一种算法让两个指针分别从A和B点往C点走,两个指针分别走到C后,又各自从另外一个指针的起点,也就是A指针第二次走从B点开始走,B指针同理,这样,A指针走的路径长度 AO + OC + BO 必定等于B指针走的路径长度 BO + OC + AO,这也就意味着这两个指针第二轮走必定会在O点相遇,相遇后也即到达了退出循环的条件,代码如下:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = Noneclass Solution:def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:index_a = headAindex_b = headBwhile index_a !=index_b:if index_a !=None:index_a = index_a.nextelse:index_a = headBif index_b != None:index_b = index_b.nextelse:index_b = headAreturn index_ac++实现:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {ListNode* node_A = headA;ListNode* node_B = headB;while(node_A!=node_B){if(node_A!=NULL){node_A=node_A->next;}else{node_A = headB;}if(node_B!=NULL){node_B=node_B->next;}else{node_B = headA;}}return node_A;}
};48.LRU 缓存机制

class DLinkedNode:def __init__(self, key=0, value=0):self.key = keyself.value = valueself.prev = Noneself.next = Noneclass LRUCache:def __init__(self, capacity):self.cache = dict()# 使用伪头部和伪尾部节点self.head = DLinkedNode()self.tail = DLinkedNode()self.head.next = self.tailself.tail.prev = self.headself.capacity = capacityself.size = 0def get(self, key):if key not in self.cache:return -1# 如果 key 存在,先通过哈希表定位,再移到头部node = self.cache[key]self.moveToHead(node)return node.valuedef put(self, key, value):if key not in self.cache:# 如果 key 不存在,创建一个新的节点node = DLinkedNode(key, value)# 添加进哈希表self.cache[key] = node# 添加至双向链表的头部self.addToHead(node)self.size += 1if self.size > self.capacity:# 如果超出容量,删除双向链表的尾部节点removed = self.removeTail()# 删除哈希表中对应的项self.cache.pop(removed.key)self.size -= 1else:# 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部node = self.cache[key]node.value = valueself.moveToHead(node)def addToHead(self, node):node.prev = self.headnode.next = self.head.nextself.head.next.prev = nodeself.head.next = nodedef removeNode(self, node):node.prev.next = node.nextnode.next.prev = node.prevdef moveToHead(self, node):self.removeNode(node)self.addToHead(node)def removeTail(self):node = self.tail.prevself.removeNode(node)return nodesol = LRUCache(2)
sol.put(1, 1)
res = sol.get(1)
print('==res:', res)49.排序链表

思路1:归并排序 先通过快慢指针找到中心点 进行截断以后一直递归拆开 在进行合并即可
python代码:
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:def merge(self, left, right):res = ListNode(0)temp = reswhile left and right:if left.val < right.val:temp.next, left = left, left.nextelse:temp.next, right = right, right.nexttemp = temp.nexttemp.next = left if left else rightreturn res.nextdef sortList(self, head: ListNode) -> ListNode:if head is None or head.next is None:return head #快慢指针找到链表中心点slow, fast = head, head.nextwhile fast and fast.next:fast, slow = fast.next.next, slow.nextmid, slow.next = slow.next, None#将找到的中心点进行截断故 slow.next = Noneleft, right = self.sortList(head), self.sortList(mid)#递归一直进行拆分return self.merge(left, right)#合并操作c++代码:
/*** Definition for singly-linked list.* struct ListNode {* int val;* ListNode *next;* ListNode() : val(0), next(nullptr) {}* ListNode(int x) : val(x), next(nullptr) {}* ListNode(int x, ListNode *next) : val(x), next(next) {}* };*/
class Solution {
public:ListNode* mergetwo(ListNode* l1,ListNode* l2){ListNode* new_head = new ListNode(0);ListNode* node = new_head;while(l1 && l2){if(l1->val<l2->val){node->next = l1;l1 = l1->next;}else{node->next = l2;l2 = l2->next;}node = node->next;}if(l1){node->next = l1;}if(l2){node->next = l2;}return new_head->next;}ListNode* sortList(ListNode* head) {if(head==nullptr || head->next==nullptr){return head;}ListNode* slow = head;ListNode* fast = head->next;while(fast && fast->next){slow = slow->next;fast = fast->next->next;}ListNode* middle = slow->next;slow->next = nullptr;ListNode* l1 = sortList(head);ListNode* l2 = sortList(middle);return mergetwo(l1,l2);}
};思路2:合并也是递归
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:# def merge(self, left, right):# res = ListNode(0)# temp = res# while left and right:# if left.val < right.val:# temp.next, left = left, left.next# else:# temp.next, right = right, right.next# temp = temp.next# temp.next = left if left else right# return res.nextdef merge(self,left,right):if left is None:return rightif right is None:return leftif left.val < right.val:left.next = self.merge(left.next, right)return leftelse:right.next = self.merge(left, right.next)return rightdef sortList(self, head: ListNode) -> ListNode:if head is None or head.next is None:return head #快慢指针找到链表中心点slow, fast = head, head.nextwhile fast and fast.next:fast, slow = fast.next.next, slow.nextmid, slow.next = slow.next, None#将找到的中心点进行截断故 slow.next = Noneleft, right = self.sortList(head), self.sortList(mid)#递归一直进行拆分return self.merge(left, right)#合并操作







转c++ tensorrt)




 + python(c++))





