安装，参考：https://blog.csdn.net/augusdi/article/details/8808226
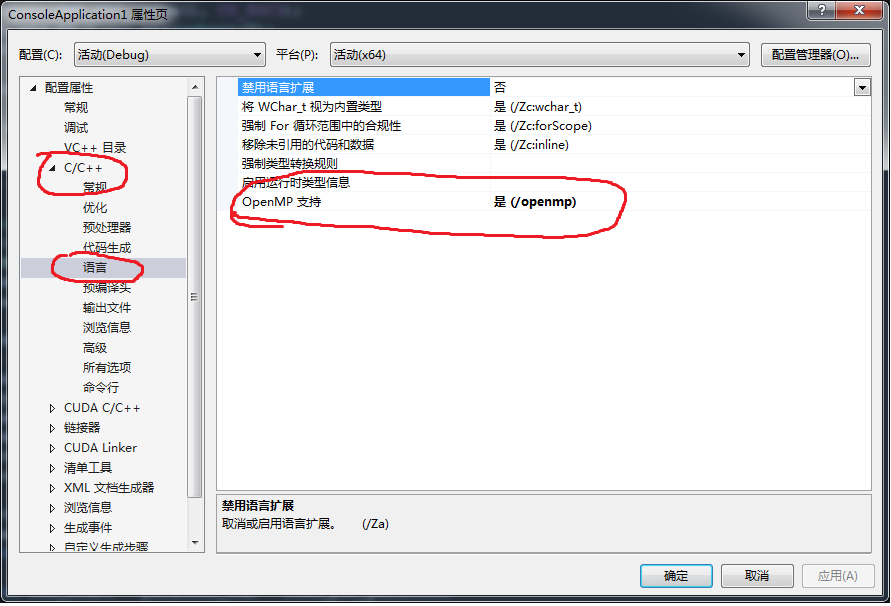
如图所示，右键工程名->属性->C/C+±>语言，找到OpenMP支持，更改设置即可。
代码编程，参考：https://blog.csdn.net/zhongkejingwang/article/details/40350027
在C/C++中使用OpenMP优化代码方便又简单，代码中需要并行处理的往往是一些比较耗时的for循环，所以下面介绍一下OpenMP中for循环的应用。
###1. 首先，如何使一段代码并行处理呢？
omp中使用parallel制导指令标识代码中的并行段，形式为：
#pragma omp parallel
{...//每个线程都会执行大括号里的代码
}
我们编写如下的代码：
#include <iostream>
#include "omp.h"
using namespace std;
int main(int argc, char **argv) {//设置线程数，一般设置的线程数不超过CPU核心数，这里开4个线程执行并行代码段omp_set_num_threads(4);#pragma omp parallel{cout << "Hello" << ", I am Thread " << omp_get_thread_num() << endl;}
}
上面的代码输出结果为：
Hello,Thread Hello,Thread 21
Hello,Thread 3
Hello,Thread 0
可以看到四个线程各自独立的输出了cout后面的内容。如果去掉omp_set_num_threads(4)语句，我们的电脑CPU的每个核都会独立执行，我的CPU有8个核，就会执行8次大括号内的语句。
###2.带有for的制导指令：
使用形式为：
#pragma omp parallel for
for()
或者
#pragma omp parallel
{ //注意：大括号必须要另起一行#pragma omp forfor()
}
第一种形式作用域只是紧跟着的那个for循环，而第二种形式在整个并行块中可以出现多个for制导指令。
...
#include "omp.h"
...
int main()
{omp_set_num_threads(4);#pragma omp parallel forfor (int i = 0; i < 6; i++){printf("i = %d,Hello,Thread:%d\n", i, omp_get_thread_num());}return 0;
}
输出结果如下：
i = 0,Hello,Thread:0
i = 1,Hello,Thread:0
i = 2,Hello,Thread:1
i = 3,Hello,Thread:1
i = 5,Hello,Thread:3
i = 4,Hello,Thread:2
我们可以看到输出6次printf的任务被分给了CPU的4个核。
###3.数据同步问题
int main()
{int n = 100000;int sum = 0;omp_set_num_threads(4);#pragma omp parallel forfor (int i = 0; i < n; i++){sum++;}cout << sum << endl;return 0;
}
期望的正确结果是100000，但是这样写是错误的。看代码，由于默认情况下sum变量是每个线程共享的，所以多个线程同时对sum操作时就会因为数据同步问题导致结果不对，显然，输出结果每次都不同，这是无法预知的，下面是输出结果，但是每个线程不会共享for循环中的变量，包括i值。所以如果线程要调用for循环外的变量，要加critical语句，下面有介绍。
//多次输出结果
58504
45203
35716
...
#####解决方法1：方法一：对操作共享变量的代码段做同步标识
int main()
{int n = 100000;int sum = 0;omp_set_num_threads(4);#pragma omp parallel forfor (int i = 0; i < n; i++){#pragma omp critical{sum++;}}cout << sum << endl;return 0;
}
critical制导语句标识的下一行代码，也可以是跟着一个大括号括起来的代码段做了同步处理。
输出结果100000。
