本系列博文是对研一课程《模式识别与机器学习》的随堂笔记,希望将老师所讲的与自己的见解记录下来,方便加深自己的理解以及以后复习查看,笔记完全按照老师所讲顺序,欢迎交流。
一、模式识别与机器学习的基本问题
机器学习主要解决以下四类问题:
1.监督学习:指的是训练的数据既包括特征(feature)又包括标签(label),通过训练,让机器可以自己找到特征和标签之间的联系,在面对只有特征没有标签的数据时,可以判断出标签。监督学习主要分为两类,分别为回归问题(Regression)与分类问题(Classification)。回归问题的目标是通过对已有数据的训练拟合出恰当的函数模型,分类问题的目标是通过分析数据的特征向量与对应类别标签的关系,对于一个新的特征向量得到其类别。两者的区别是回归针对连续数据,分类针对离散数据。
2.非监督学习:指的是在未加标签的数据中,找到隐藏的结构,由于提供给学习者的实例是未标记的,因此没有错误信号(损失)来评估潜在的解决方案。典型的非监督学习类型包括聚类(Cluster)、隐马尔可夫模型、使用特征提取的技术降维(主成分分析)。
3.半监督学习:所给的数据有的是有标签的,而有的是没有标签的,试图利用大量的未标记示例来辅助对少量有标记示例的学习,常见的两种半监督的学习方式是直推学习(Transductive learning)和归纳学习(Inductive learning)。
4.强化学习(Reinforcement learning):指的是机器以“试错”的方式进行学习,通过与环境交互获得奖赏指导行为,目标是使机器获得最大的奖赏。强化学习中由环境提供的强化信号对产生动作的好坏作评价,而不是告诉机器如何去产生正确的动作。
二、多项式曲线拟合(Polynomial Curve Fitting)实例
本课程讲述的机器学习算法多为监督学习算法和非监督学习算法,此处用多项式曲线拟合的例子来简述监督学习的过程,作为全文开篇的算法来讲解机器学习的共通性。
1.问题描述
输入变量:x ,目标变量:t , 生成过程:实际问题中是未知的 , 给定训练样本:x,t
前文讲述过监督学习是指训练的数据既包括特征,又包括标签。在本例中,输入变量x即为数据特征,目标变量t即为标签,我们给定训练样本:x,t。生成过程也就是我们将使用的带有参数的待拟合模型(实际问题中是未知的,需要根据人为的经验选取合适的模型),本例中采用的模型为多项式模型,公式如下,
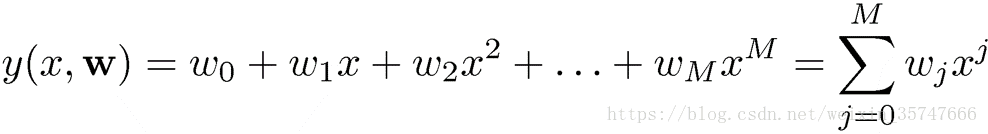
我们的目标是当给定新的x值时,能够通过此模型预测t的值,也就是说,我们需要利用给定的训练样本,估计模型中的参数w。如何计算出最佳的w值?采用误差平方和最小的原理,即
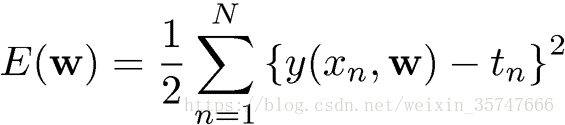
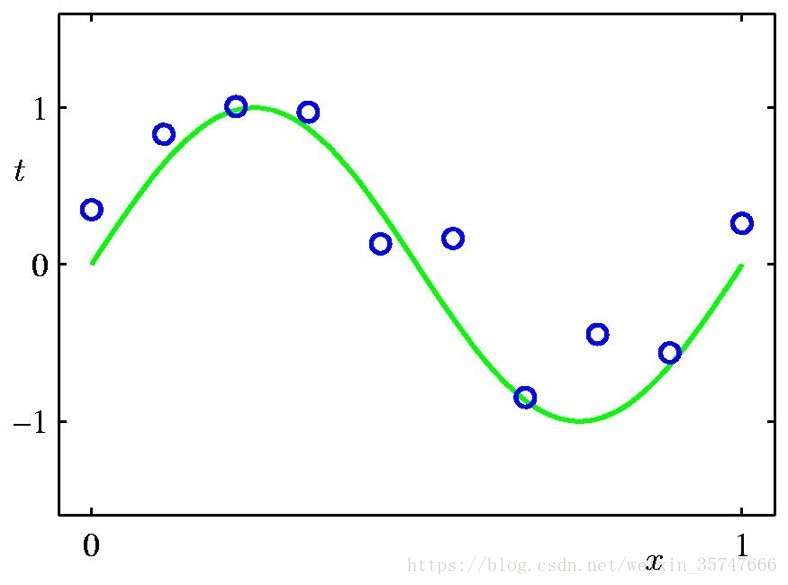

2.求解问题
问题中,参数w的个数M是模型的关键,我们假定有10个训练样本,分别取M=0,1,3,9来观察模型的拟合情况。
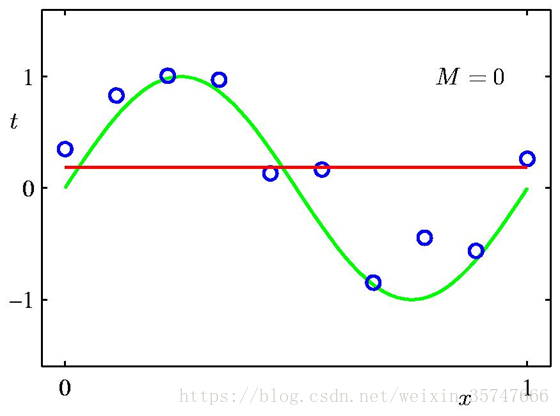

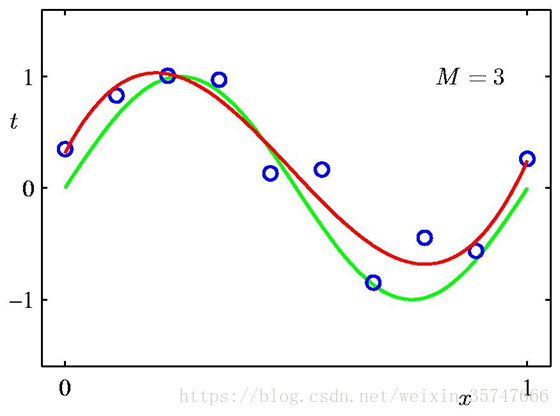
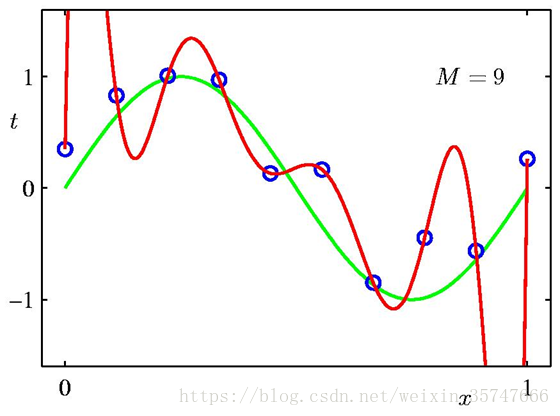
当M=0,1时,模型的效果很差,很多点不在曲线上;当M=3时,模型效果良好,红色线与绿色线基本一致;当M=9时,虽然所有训练数据均在曲线上,但模型效果极差,红色线与绿色线差别极大(10个方程,9个未知数,相当于模型有确定的解),这种情况称为过拟合(Over-fitting),与之相对应的是欠拟合(Under-fitting)。我们对M取值的不同情况进行考察,得到如下的结果,
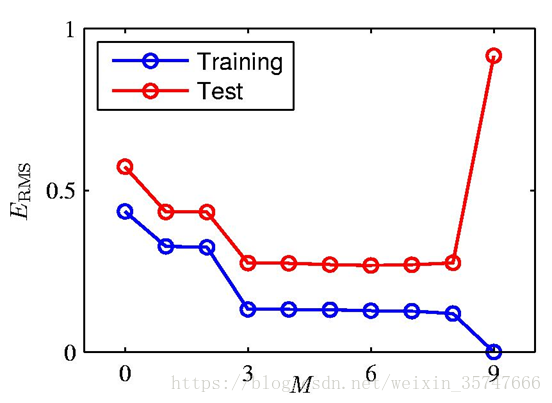
此处的ERMSE_{RMS}ERMS为均方误差(root-mean-square),
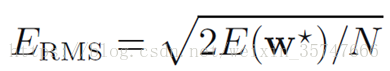
当M=9时,此时的训练误差很小(为零),而测试误差很大,这种情况我们称为过拟合;相对应的,欠拟合是由于训练量少导致的训练误差很大的情况。可见,当参数数量很多时,接近或超过训练数据的数量,会导致过拟合,也就是说,模型复杂度越高过拟合越容易发生。对于一个模型来说,如果它能够对没见过的数据做出预测,我们就说它能够从训练集泛化到测试集,我们的目标是构造出泛化精度尽可能高的模型。在欠拟合与过拟合间存在一个最佳泛化模型,
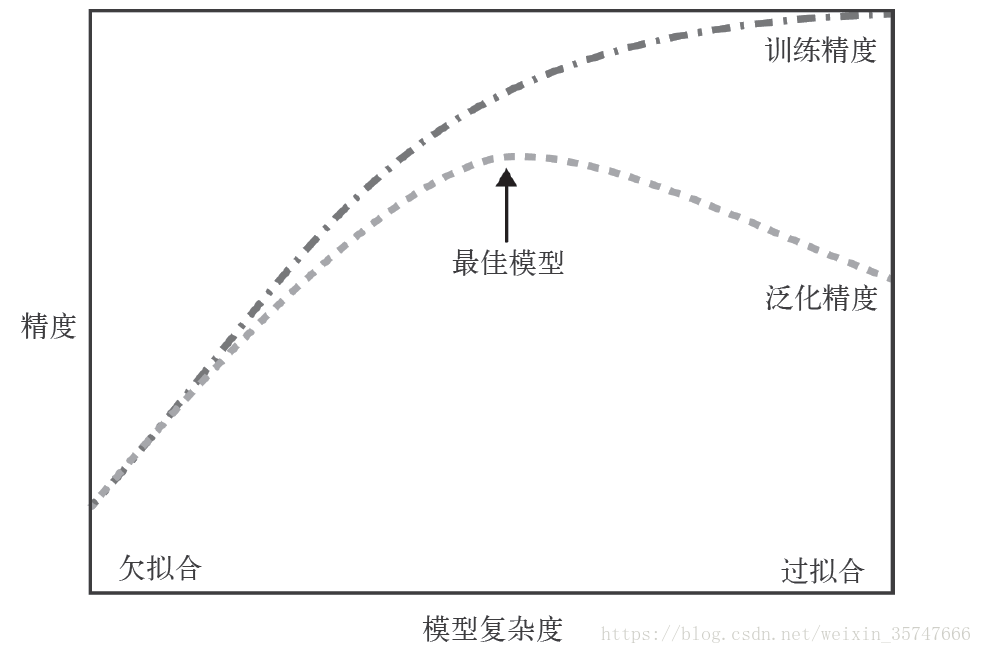
上述是采用10个训练样本和9个模型参数的情况,我们尝试增加训练样本的数量,观察训练结果,
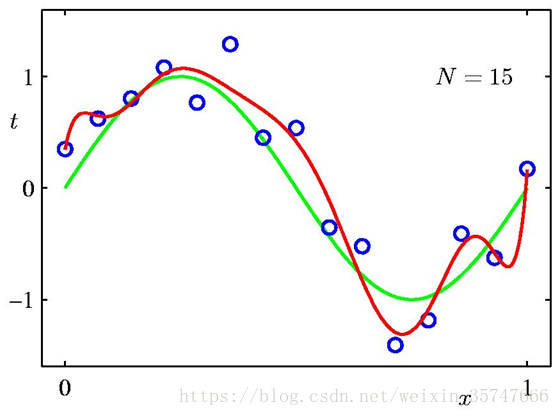
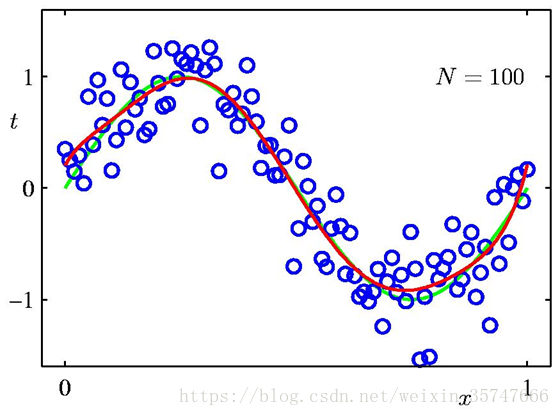
我们发现,训练样本数量越多,模型的拟合效果越好,同时解决了过拟合的问题,说明增加数据集有效地解决了模型复杂度过高导致的过拟合问题。由此可以看出,模型复杂度与训练集输入的变化密切相关,当我们选择模型时,数据集中包含的数据点的变化范围越大,在不发生过拟合的前提下可以使用的模型就越复杂。
观察训练后的模型参数,发生过拟合情况下的参数往往非常大,原因是拟合函数需要考虑每一个训练样本点,最终形成的拟合函数波动很大,在某些很小的区间里函数值的变化很剧烈,意味着在某些区间的函数导数值的绝对值会非常大,只有参数(系数)足够大,导数的绝对值才能更大。

为了约束参数的范围,采用正则化 的方法,可以在一定程度上减少过拟合的情况。
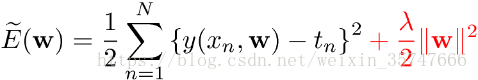
在损失函数尾部所加的计算式即为正则项,直观上来看正则项缓解了www的变化,可以假设当E(w)E(w)E(w)有同样的ΔE(w)ΔE(w)ΔE(w)时,由于正则项始终为正,分担了一部分的E(w)E(w)E(w)的变化,相对于不加上正则项,减缓了由于原损失函数项C0C_0C0导致的www的变化(个人理解)。严格的数学推导如下,
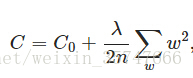
CCC为添加正则项后的损失函数,采用梯度下降法进行求解,
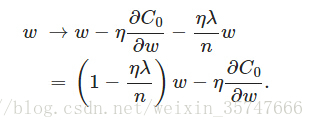
其中,η、λ、nη、λ、nη、λ、n都是正的,所以 1−ηλ/n1−ηλ/n1−ηλ/n小于1,它的效果是减小www(直接减小了www的值,防止过大或过小,限制www的范围)。
λλλ是超参数,需要人为设置,当λ=0λ=0λ=0时相当于不加入正则项,设置不同的λλλ有如下不同的结果,
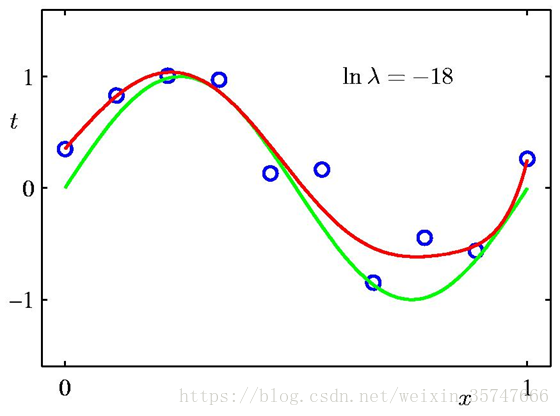
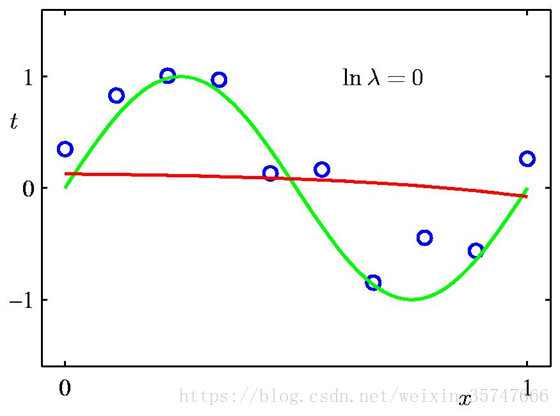
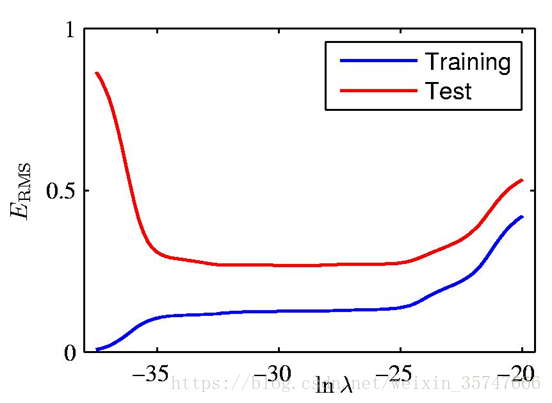
模型参数值如下,

正则化有效的缓解了模型的过拟合问题,解决途径:添加正则项→限制参数→解决过拟合。
未完待续

)
机器学习的基础理论)


)


概述)

图像变换)



图像增强1)
图像增强2)



图像增强3)