1 变换过程
照相机的成像变换过程可以分为3步:世界坐标系——>相机坐标系——>图像坐标系——>像素坐标系
2 世界坐标系——>相机坐标系
景物从世界坐标系转换到相机坐标系需要使用到刚体变换(物体不发生变形,对一个几何物体做旋转或平移)

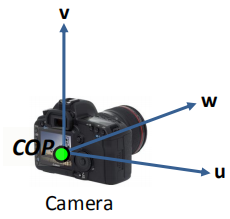
刚体变换如下图所示:
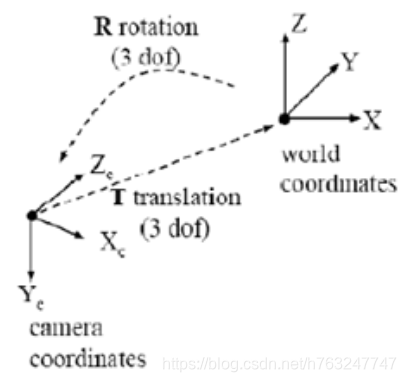
变换的数学表达式为:
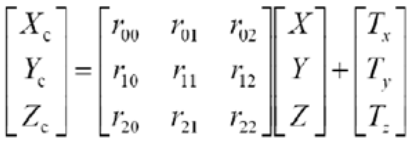
简化:
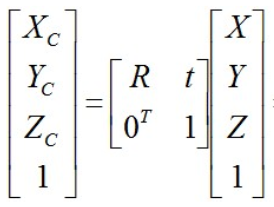
其中,代表相机坐标系,
代表世界坐标系,
矩阵代表旋转变换,向量
代表平移。
称为相机的外参数,与相机无关。
旋转变换由3种变换组成:绕 x 轴旋转,绕 y 轴旋转和绕 z 轴旋转,用公式表示为:
其中分别表示绕 x 轴旋转,绕 y 轴旋转和绕 z 轴旋转的旋转矩阵。
3 相机坐标系——>图像坐标
此变换通过小孔成像实现,其原理如下图所示:
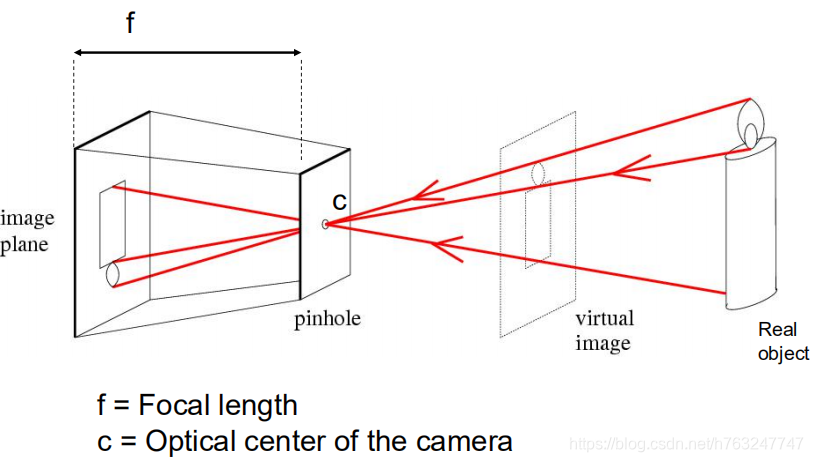
简化其投影过程,
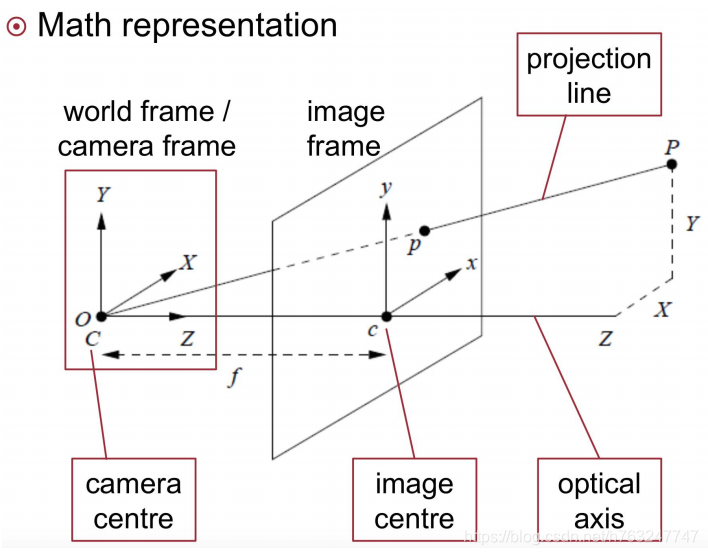
已知位于相机坐标系的一个点, 投影到图像的点
,由相似三角形:

可得:
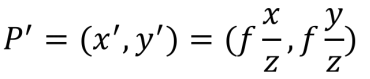
用矩阵表示:
4 图像坐标系——>像素坐标系
下方图像标注了两种坐标系:
表示图像坐标系,其坐标是连续的;
代表像素坐标系,其坐标只能是大于零的整数,中心像素点的坐标为
,
每一个像素点的长宽为:dx, dy, 即为感光芯片上像素的实际大小。
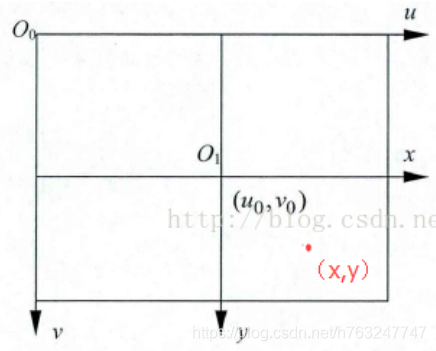
从图像坐标系到像素坐标系的变换公式为:
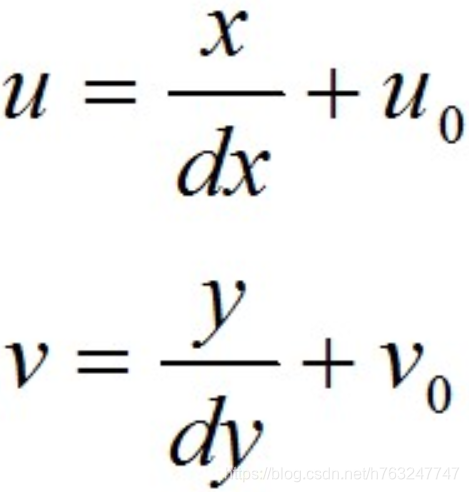
用矩阵表示:
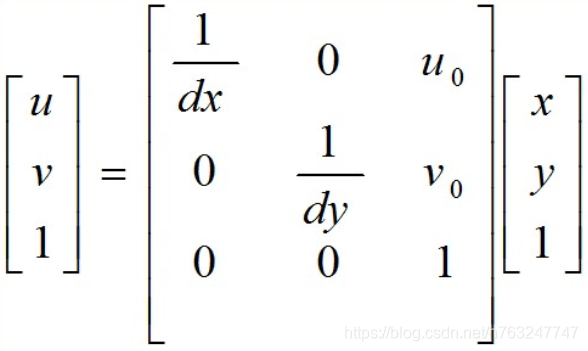
5 相机坐标系——>像素坐标系
综合3和4两部分,隐去图像坐标系,直接求取从相机坐标系到像素坐标系的变换矩阵
为了去掉z,转换为其次矩阵
简化:
其中
K 为相机的矫正矩阵(calibration matrix)
如果算入图像的倾斜度K为:
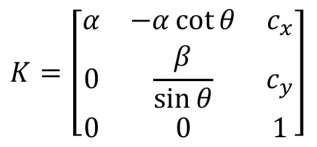
这里的cx,cy即为u0, v0
6 世界坐标系——>像素坐标系
由2和5部分的分析,可得:
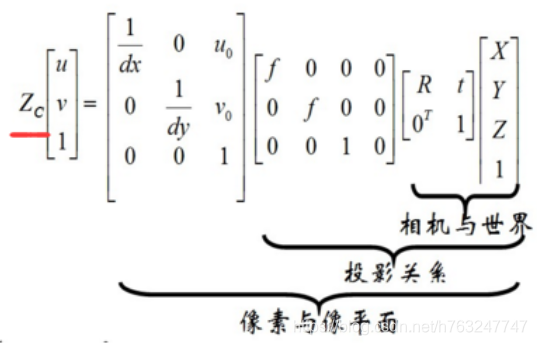
简化:

M 为一个3*4的矩阵,11个未知参数,其中
5个未知参数来自内参矩阵(intrinsic matrix)
3个来自外参旋转
3个来自外参平移
)




-本征矩阵(essential matrix)和基本矩阵(fundamental matrix))









)



)