1 何为 Imbalanced class problem

在分类问题中，有时候一种类别的数据会远远的多于另外一种类别，

但正是这些少量的类别的数据，往往又是极其重要的。

比如信用卡欺诈事件，该事件远远地小于信用卡未被欺诈的事件。

要从信用卡操作的数据中，识别出欺诈这一类别的事件，比例极其小，但确是及其重要的。

在大量的操作数据中找到欺诈事件，犹如大海捞针。

这个时候如果继续使用精度来评估分类器就不准确了。

因为即使把所有的信用卡操作数据，都判断为未欺诈类别，

其正确率也可以达到99.999......%，这种分类器明显是无用的。

针对Imbalanced class problem, 研究者提出了许多其它的参数来评估模型。

 

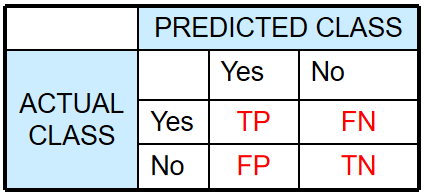
2 Confusion Matrix

2.1 相关概念

在Confusion Matrix中，

    

由Confusion Matrix 定义一些参数：

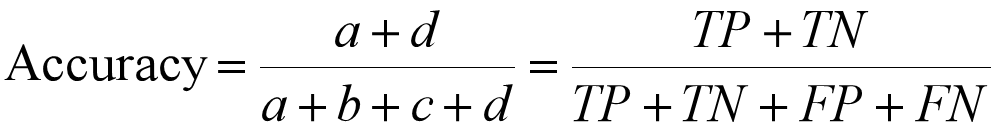
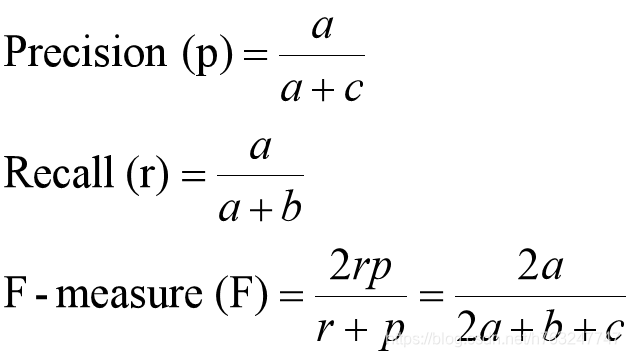
2.2 计算实例

实例中的分类器，虽然正确率达到了99.1%，但是Recall参数只有0.1， 对于class=Yes 类别的预测，

正确率只有10%，非常低。

2.3 分类问题的拓展参数

还是类似的的confusion matrix

 

3 ROC（Receiver Operating Characteristic）

ROC 发展于20世纪50年代的信号检测理论, 用于显示检测率和误报警率之间的权衡。

ROC曲线显示TPR与FPR的关系，用ROC曲线上的一个点表示模型的性能，

改变分类器的阈值参数会改变点的位置

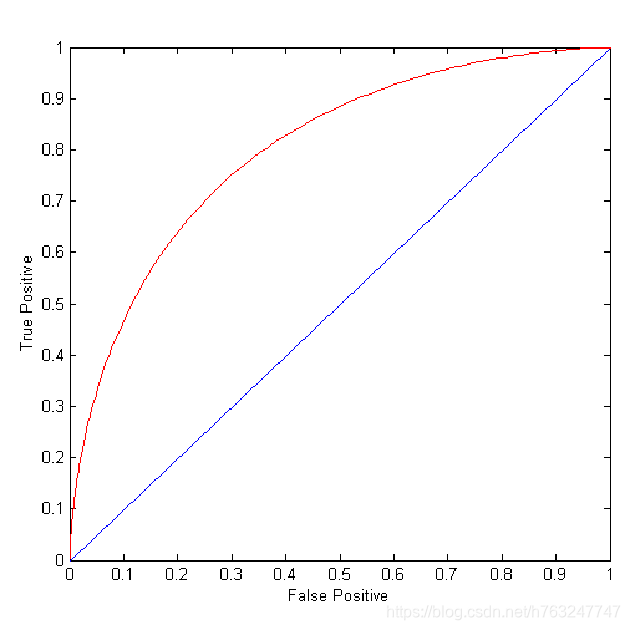
（TPR，FPR）

• （0，0）：把所有数据判别为负类；
• （1，1）：把所有数据判别为正类；
• （1，0）：理想情况

对角线是一条假想线，低于该线表示于正确的类别相反。

 

4 基于ROC的模型比较

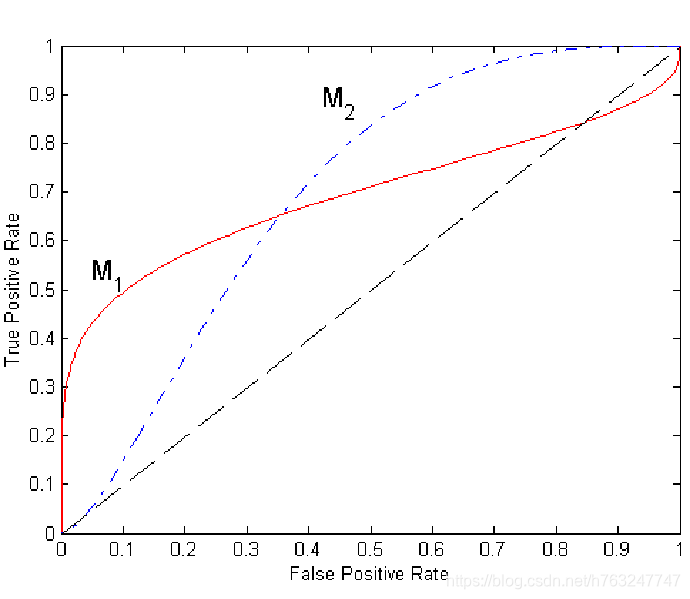
没有一种模型总是好于另一种

上图中，对于小的FPR值，M1 更好

对于大的FPR值，M12更好

 

5 如何构建一个ROC曲线

• 为每个实例，使用分类器产生一个连续值的分数，该实例在+ class 的可能性越高，得分越高
• 根据分数，按照降序排列实例
• 应用一个阈值在每个独特价分数值
• 在每个阈值计算TPFP, TN, FN的数量,

TPR = TP / (TP + FN)

FPR= FP / (FP + TN)