1 物体深度

问题描述：从不同的位置拍摄相同物体的两张图片，恢复其深度

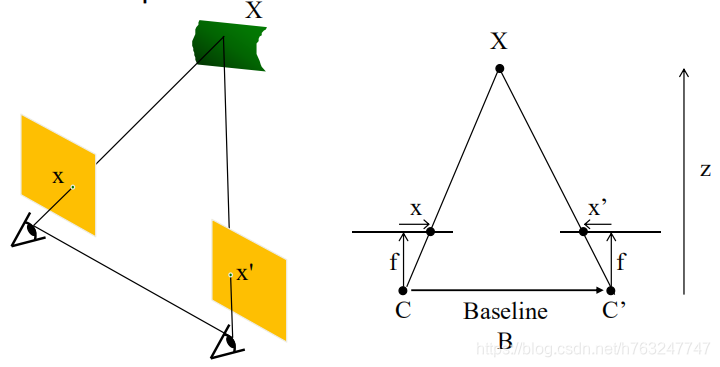
这里假设摄像机的镜头平行

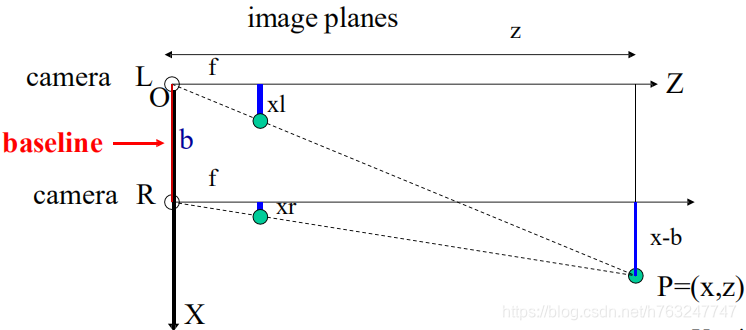
由相似三角形：

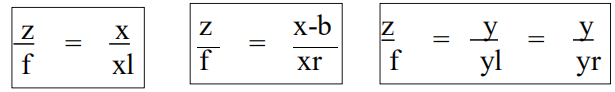
由上面第一、二等式可得：

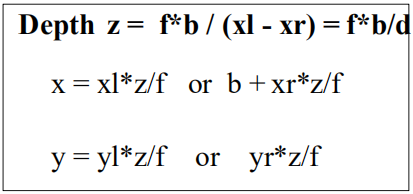
深度与视差成反比

 

2 如何配对左右图片的点

问题描述：已知两张图像，由不同的照相机拍下，在左图中选一点，

如何在右图中找到对应的点。

由上图可知，

左图中点 x 对应在右图中的点位于线段 l' 上

右图中点 x‘ 对应在左图中的点位于线段 l 上

2.1 极线几何（epipolar geometry）的基本概念

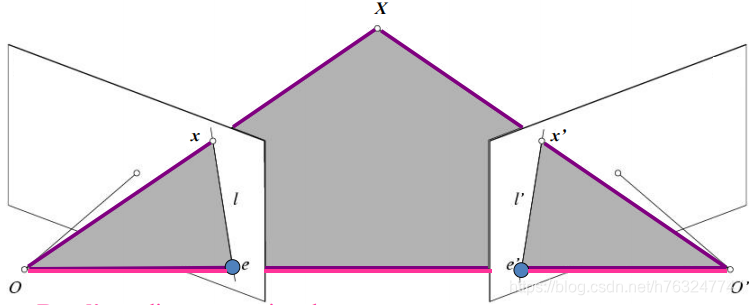
• 基线（baseline）: 连接两个照相机中心点的线段，如图中的OO'。
• 极平面（epipolar plane）: 由两个相机中心点, 和物体X组成的平面，如图中的OO'X。
• 极点（epipoles）: 基线与两张图像的交点，如图中的e, e'。
• 极线（epipolar lines）: 极平面与两张图像的交线，如图中的 l ，l'。

2.2 极线约束（epipolar constraint）

2.2.1 calibrated case

这种情况，相机的内参和外参已知，极线几何工作在一对归一化相机（normalized camera）.

归一化相机（normalized camera）使形成的归一化图像平面位于Z=1处。

图像归一化（ image normalization）是指对图像进行了一系列标准的处理变换，使之变换为一固定标准形式的过程。

归一化的图像可以减少几何变换的影响，加快梯度下降求最优解的速度。

在世界坐标系中，如果把一个相机位于原点，另一个相机的位置可以通过旋转和平移得到。

两者关系如下图所示，右边相机的位置可以通过旋转（R）和平移（T）得到。

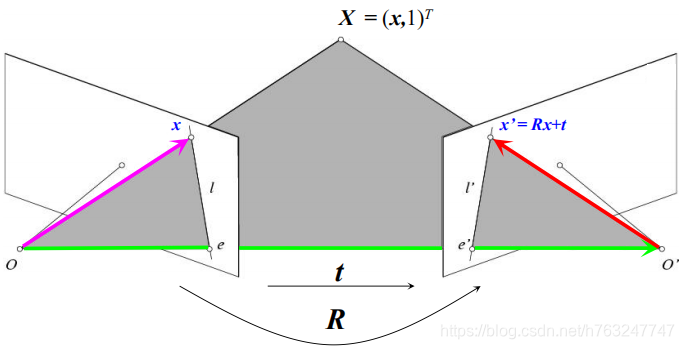
从上图可知： 向量Rx， 位移 t 和 点 x' 共面，所以：

其中矩阵 E 为本征矩阵（essential matrix）

由于 矩阵 [ tx] 的秩为2， 矩阵R的秩为3，所以 E 的秩为2. 

E有5个未知数（2个平移，3个旋转）。

在向量的叉乘运算中，把第一个向量写成矩阵的形式：

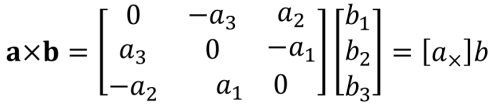
其中矩阵 [ax] 的秩为2.

假设右边图像上点x'=（u', v'）

穿过点 x' 的 直线 l' 可以表示为：au’+bv'+c=0;

其中沿直线 l' 的向量可以表示为：

所以  或 

• ，即左图中点 x 对应的右图中的点 x' 位于线段 l' 上
• 同理， ,即右图中点 x‘ 对应的左图中的点 x 位于线段 l 上
•  
• 

2.2.2 Uncalibrated case

在这种情况下，两个相机的内参矩阵 K 和 K’ 未知。

从相机坐标系到像素坐标系的对应关系：

其中  为像素点坐标， 为相机坐标系的坐标， 为内参矩阵。

代入上式：

化简：

令 

则：

F 称为基本矩阵（fundamental matrix）

与calibrated case 类似，uncalibrated case也有类似的结论：

• , 即左图中像素点 x 对应的右图中的像素点 x' 位于线段 l' 上
• , 即右图中像素点 x‘ 对应的左图中的像素点 x 位于线段 l 上
• 
• 

如果觉得上面的推论有跳跃性，下面链接的博客推导非常详细：

计算机视觉基础4——对极几何(Epipolar Geometry)

计算机视觉基础5——本质矩阵与基本矩阵(Essential and Fundamental Matrices)

 

3 求解基本矩阵（fundamental matrix）

已知两对点：

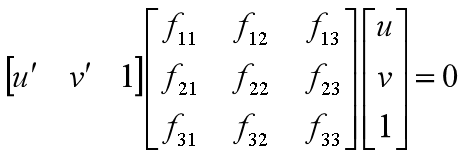
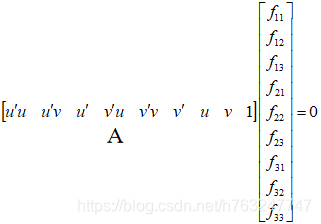
转化为凸优化问题：

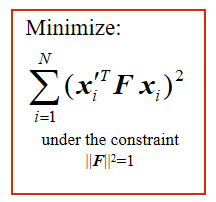
其解为：的最小特征值的特征向量。