定义:
主成分分析(Principal Component Analysis,PCA), 是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。PCA的思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征。这k维特征称为主成分,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余n-k维特征。
简单解释:
具体的,假如我们的数据集是n维的,共有m个数据。我们希望将这m个数据的维度从n维降到k维,希望这m个k维的数据集尽可能的代表原始数据集。我们知道数据从n维降到k维肯定会有损失,但是我们希望损失尽可能的小。那么如何让这k维的数据尽可能表示原来的数据呢?
我们先看看最简单的情况,也就是n=2,k=1,也就是将数据从二维降维到一维。数据如下图。我们希望找到某一个维度方向,它可以代表这两个维度的数据。图中列了两个向量方向,u1和u2,那么哪个向量可以更好的代表原始数据集呢?从直观上也可以看出,u1比u2好,因为数据在这个方向上投影后的样本点之间方差最大。

例子:
有两维数据:
![]()
对X进行归一化,使X每一行减去其对应的均值,得到:
![]()
求X的协方差矩阵:
![]()
求解C的特征值,利用线性代数知识或是MATLAB中eig函数可以得到:
![]()
![]()
对应的特征向量分别是:
![]()
![]()
将原数据降为一维,选择最大的特征值对应的特征向量,因此P为:
![]()
降维后的数据:
![]()
那么,为什么要求特征值和特征向量呢?
特征值和特征向量:
转自https://blog.csdn.net/fuming2021118535/article/details/51339881
定义: 设A是n阶矩阵,如果数λ和n维非零向量x使关系式
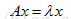
成立,那么,这样的数λ称为矩阵A的特征值,非零向量x称为A的对应于特征值λ的特征向量,(1)式还可以写为
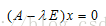
如果想求出矩阵对应的特征值和特征向量就是求式(2)的解了。
那么,问题来了,这个式子要怎么理解呢?
首先得先弄清矩阵的概念:一个矩阵代表的是一个线性变换规则,而一个矩阵的乘法运行代表的是一个变换;
比如有一个矩阵A:
一个列向量为X为:
一个矩阵的乘法为:
向量X通过矩阵A这个变化规则就可以变换为向量Y了

知道了这个就可以从几何上理解特征值和特征向量是什么意思了,由
可知:
所以,确定了特征值之后,向量x的变换为:

引用《线性代数的几何意义》的描述:“矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。”
那么这样定义的特征值和特征向量有什么实际用途呢?在这里我举个数据挖掘算法中重要的一个算法:PCA(主成分分析)来给大家直观的感受一下。
首先,理解一下信息量这个概念
看几张图:

如果我们单独看某一个维度的话,比如看x1这个维度

可以看到将点投影到x1这个维度上看的话,图1的数据离散性最高,图3较低,图2数据离散性是最低的。数据离散性越大,代表数据在所投影的维度上具有越高的区分度,这个区分度就是信息量。如果我们用方差来形容数据的离散性的话,就是数据方差越大,表示数据的区分度越高,也就是蕴含的信息量是越大的。
基于这个知识,如果我们想对数据进行降维的话,比如图1的两个维度的数据降成一维,我们可以选择保留X1这个维度的数据,因为在这个维度上蕴含的信息量更多。
同理,图2就可以保留x2这个维度的数据。但是,问题来了,图3应该保留哪个维度的数据呢?答案是保留哪个维度都不好,都会丢失较大的信息量。但是,如果我们把图3的坐标轴旋转一下

比较容易看出,图3在新的坐标轴下就能进行降维了。所以选取正确的坐标轴,然后根据各个维度上的数据方差大小,决定保留哪些维度的数据,这样的做法就是主成分分析的核心思想。
选取正确的坐标轴的过程中,我们需要一个矩阵变换,就类似于这样:
也就是:
其实,经过数学上的推导的,我们就可以知道,特征值对应的特征向量就是理想中想取得正确的坐标轴,而特征值就等于数据在旋转之后的坐标上对应维度上的方差。
也就是说,直接求出矩阵A的特征向量得出对应的特征向量。我们就能找到旋转后正确的坐标轴。这个就是特征值和特征向量的一个实际应用:“得出使数据在各个维度区分度达到最大的坐标轴。”
所以,在数据挖掘中,就会直接用特征值来描述对应特征向量方向上包含的信息量,而某一特征值除以所有特征值的和的值就为:该特征向量的方差贡献率(方差贡献率代表了该维度下蕴含的信息量的比例)。
通常经过特征向量变换下的数据被称为变量的主成分,当前m个主成分累计的方差贡献率达到一个较高的百分数(如85%以上)的话,就保留着这m个主成分的数据。实现了对数据进行降维的目的。整个主成分分析的算法原理也就是这个。
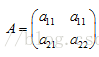
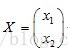
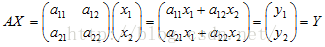

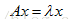
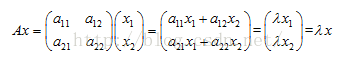

代码)




)

)
)
代码)


)






)