吴恩达《机器学习》学习笔记十四——应用机器学习的建议实现一个机器学习模型的改进

一、任务介绍
二、代码实现
- 1.准备数据
- 2.代价函数
- 3.梯度计算
- 4.带有正则化的代价函数和梯度计算
- 5.拟合数据
- 6.创建多项式特征
- 7.准备多项式回归数据
- 8.绘制学习曲线
- - 𝜆=0
  - 𝜆=1
  - 𝜆=100
- 9.找到最佳的 𝜆

前几次笔记介绍了具体实现一个机器学习模型的时候应该如何操作，首先是快速实现一个较为简单的模型，然后通过绘制学习曲线去判断目前的模型存在什么问题，分析应该如何改进，这次笔记就将实现这一整个过程。

数据集：https://pan.baidu.com/s/1Er82YunOOmyTJIW-0H40mQ
提取码：41rj

一、任务介绍

这次笔记中我们将要实现正则化线性回归，并用它来研究带有方差-偏差性质的模型。首先使用正则化线性回归，通过水位（water_level）的改变来预测一个大坝的出水量（flow），然后通过绘制学习曲线来诊断学习算法存在的问题，分析是具有偏差还是具有方差，以及如何调节。

二、代码实现

1.准备数据

import numpy as np
import scipy.io as sio
import scipy.optimize as opt
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

def load_data():"""for ex5d['X'] shape = (12, 1)pandas has trouble taking this 2d ndarray to construct a dataframe, so I ravelthe results"""d = sio.loadmat('ex5data1.mat')return map(np.ravel, [d['X'], d['y'], d['Xval'], d['yval'], d['Xtest'], d['ytest']])

把训练集、验证集和测试集都读入了，然后观察一下他们的维度：

X, y, Xval, yval, Xtest, ytest = load_data()
print('X:', X.shape)
print('Xval:', Xval.shape)
print('Xtest:', Xtest.shape)

在这里插入图片描述
可以看到训练集、验证集和测试集分别有12、21、21个数据。

下面对训练数据可视化，对它有个直观的理解：

df = pd.DataFrame({'water_level':X, 'flow':y})sns.lmplot('water_level', 'flow', data=df, fit_reg=False, size=7)
plt.show()

在这里插入图片描述
最后是需要为三个数据集的X都插入偏置，这是线性回归假设函数的常数项，也是与参数theta0相乘的项，接着再观察一下维度：

X, Xval, Xtest = [np.insert(x.reshape(x.shape[0], 1), 0, np.ones(x.shape[0]), axis=1) for x in (X, Xval, Xtest)]
print('X:', X.shape)
print('Xval:', Xval.shape)
print('Xtest:', Xtest.shape)

在这里插入图片描述

2.代价函数

线性回归的代价函数如下图所示：
在这里插入图片描述
相应的代码实现如下所示：

def cost(theta, X, y):
# INPUT：参数值theta，数据X,标签y
# OUTPUT：当前参数值下代价函数
# TODO：根据参数和输入的数据计算代价函数# STEP1：获取样本个数m = X.shape[0]# STEP2：计算代价函数inner = X @ theta - ysquare_sum = inner.T @ innercost = square_sum / (2 * m)return cost

给一个初始参数计算的玩玩，注意参数theta的维度：

theta = np.ones(X.shape[1])
cost(theta, X, y)

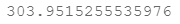
在这里插入图片描述

3.梯度计算

线性回归的梯度计算公式如下所示：
在这里插入图片描述
代码实现如下所示：

def gradient(theta, X, y):
# INPUT：参数值theta，数据X,标签y
# OUTPUT：当前参数值下梯度
# TODO：根据参数和输入的数据计算梯度  # STEP1：获取样本个数m = X.shape[0]# STEP2：计算代价函数grad=  (X.T @ (X @ theta - y))/mreturn grad

gradient(theta, X, y)

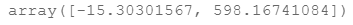
在这里插入图片描述

4.带有正则化的代价函数和梯度计算

带有正则化的梯度计算公式如下图所示：
在这里插入图片描述

def regularized_gradient(theta, X, y, l=1):
# INPUT：参数值theta，数据X,标签y
# OUTPUT：当前参数值下梯度
# TODO：根据参数和输入的数据计算梯度 # STEP1：获取样本个数m = X.shape[0]# STEP2：计算正则化梯度regularized_term = theta.copy()  # same shape as thetaregularized_term[0] = 0  # don't regularize intercept thetaregularized_term = (l / m) * regularized_termreturn gradient(theta, X, y) + regularized_term

regularized_gradient(theta, X, y)

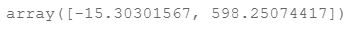
在这里插入图片描述
带有正则化的代价函数公式如下所示：

def regularized_cost(theta, X, y, l=1):m = X.shape[0]regularized_term = (l / (2 * m)) * np.power(theta[1:], 2).sum()return cost(theta, X, y) + regularized_term

5.拟合数据

def linear_regression_np(X, y, l=1):
# INPUT：数据X,标签y，正则化参数l
# OUTPUT：当前参数值下梯度
# TODO：根据参数和输入的数据计算梯度 # STEP1：初始化参数theta = np.ones(X.shape[1])# STEP2：调用优化算法拟合参数res = opt.minimize(fun=regularized_cost,x0=theta,args=(X, y, l),method='TNC',jac=regularized_gradient,options={'disp': True})return res

调用拟合数据的函数来优化参数：

theta = np.ones(X.shape[0])final_theta = linear_regression_np(X, y, l=0).get('x')print(final_theta)

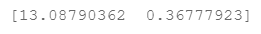
在这里插入图片描述
这就是用训练数据拟合后的theta0和theta1，下面我们对这个参数组合得到的模型来进行可视化。

b = final_theta[0] # intercept
m = final_theta[1] # slopeplt.scatter(X[:,1], y, label="Training data")
plt.plot(X[:, 1], X[:, 1]*m + b, label="Prediction")
plt.legend(loc=2)
plt.show()

在这里插入图片描述
对训练数据都不能很好的拟合，显然是欠拟合的。但这个例子太明显了，有些情况可能观察这个图不能直接判断，所以最好还是绘制学习曲线，也就是用训练数据的子集去拟合模型，得到的参数同样用来计算验证集上的误差，随着训练数据逐渐增多，计算训练误差和验证集误差并绘制出相应的曲线：

1.使用训练集的子集来拟合模型

2.在计算训练代价和交叉验证代价时，没有用正则化

3.记住使用相同的训练集子集来计算训练代价

training_cost, cv_cost = [], []

# TODO：计算训练代价和交叉验证集代价
# STEP1：获取样本个数，遍历每个样本
m = X.shape[0]
for i in range(1, m+1):# STEP2：计算当前样本的代价res = linear_regression_np(X[:i, :], y[:i], l=0)tc = regularized_cost(res.x, X[:i, :], y[:i], l=0)cv = regularized_cost(res.x, Xval, yval, l=0)# STEP3：把计算结果存储至预先定义的数组training_cost, cv_cost中training_cost.append(tc)cv_cost.append(cv)

plt.plot(np.arange(1, m+1), training_cost, label='training cost')
plt.plot(np.arange(1, m+1), cv_cost, label='cv cost')
plt.legend(loc=1)
plt.show()

在这里插入图片描述
从这个图可以看出，训练集误差和验证集误差都是比较大的，这是一种欠拟合的情况。

6.创建多项式特征

因为模型欠拟合，所以不能使用简单的线性函数来拟合了，应该添加一些多项式特征来增加模型的复杂性。

def prepare_poly_data(*args, power):"""args: keep feeding in X, Xval, or Xtestwill return in the same order"""def prepare(x):# 特征映射df = poly_features(x, power=power)# 归一化处理ndarr = normalize_feature(df).as_matrix()# 添加偏置项return np.insert(ndarr, 0, np.ones(ndarr.shape[0]), axis=1)return [prepare(x) for x in args]

特征映射之前写过，这里不再赘述，直接上代码：

def poly_features(x, power, as_ndarray=False):  #特征映射data = {'f{}'.format(i): np.power(x, i) for i in range(1, power + 1)}df = pd.DataFrame(data)return df.as_matrix() if as_ndarray else df

尝试一下上面的代码，构造一下次数最高为3的多项式特征：

X, y, Xval, yval, Xtest, ytest = load_data()

poly_features(X, power=3)

在这里插入图片描述

7.准备多项式回归数据

扩展特征到 8阶,或者你需要的阶数
使用归一化来合并x^n
不要忘记添加偏置项

def normalize_feature(df):"""Applies function along input axis(default 0) of DataFrame."""return df.apply(lambda column: (column - column.mean()) / column.std())

X_poly, Xval_poly, Xtest_poly= prepare_poly_data(X, Xval, Xtest, power=8)
X_poly[:3, :]

在这里插入图片描述

8.绘制学习曲线

𝜆=0

首先，没有使用正则化，所以 𝜆=0

def plot_learning_curve(X, y, Xval, yval, l=0):
# INPUT：训练数据集X,y，交叉验证集Xval，yval，正则化参数l
# OUTPUT：当前参数值下梯度
# TODO：根据参数和输入的数据计算梯度 # STEP1：初始化参数，获取样本个数，开始遍历training_cost, cv_cost = [], []m = X.shape[0]for i in range(1, m + 1):# STEP2：调用之前写好的拟合数据函数进行数据拟合res = linear_regression_np(X[:i, :], y[:i], l=l)# STEP3：计算样本代价tc = cost(res.x, X[:i, :], y[:i])cv = cost(res.x, Xval, yval)# STEP3：把计算结果存储至预先定义的数组training_cost, cv_cost中training_cost.append(tc)cv_cost.append(cv)plt.plot(np.arange(1, m + 1), training_cost, label='training cost')plt.plot(np.arange(1, m + 1), cv_cost, label='cv cost')plt.legend(loc=1)

plot_learning_curve(X_poly, y, Xval_poly, yval, l=0)
plt.show()

在这里插入图片描述
从这个学习曲线看，训练误差太低了，而验证集误差不算低，这是过拟合的情况（lamda=0，所以也没有任何抑制过拟合的作用，而多项式次数又比较高，过拟合很正常）。

𝜆=1

plot_learning_curve(X_poly, y, Xval_poly, yval, l=1)
plt.show()

在这里插入图片描述
训练误差稍有增加，验证误差也降得较低，算是比较好的情况。

𝜆=100

plot_learning_curve(X_poly, y, Xval_poly, yval, l=100)
plt.show()

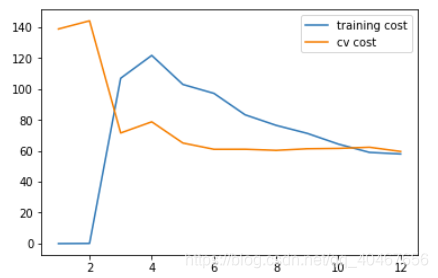
在这里插入图片描述
正则化过多，变成了欠拟合情况。

9.找到最佳的 𝜆

l_candidate = [0, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10]
training_cost, cv_cost = [], []

for l in l_candidate:res = linear_regression_np(X_poly, y, l)tc = cost(res.x, X_poly, y)cv = cost(res.x, Xval_poly, yval)training_cost.append(tc)cv_cost.append(cv)

plt.plot(l_candidate, training_cost, label='training')
plt.plot(l_candidate, cv_cost, label='cross validation')
plt.legend(loc=2)plt.xlabel('lambda')plt.ylabel('cost')
plt.show()

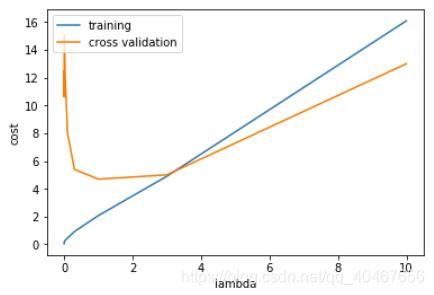
在这里插入图片描述
找出最佳的 𝜆，即找出验证误差最小时对应的 𝜆：

# best cv I got from all those candidates
l_candidate[np.argmin(cv_cost)]

在这里插入图片描述
用测试集去计算这些𝜆情况下的测试误差，最终的目的是要测试误差小：

# use test data to compute the cost
for l in l_candidate:theta = linear_regression_np(X_poly, y, l).xprint('test cost(l={}) = {}'.format(l, cost(theta, Xtest_poly, ytest)))