来源：机器之心

编辑：nhyilin

多年来，数学家们一直使用计算机来生成数据以帮助搜索数学模式，这种被称为实验数学的研究方法产生出许多重要的猜想，例如BSD猜想。虽然这种方法已经取得成功并且相当普遍，但从这些数据中识别和发现数学模式仍然主要依赖于数学家。

随着计算机领域的飞速发展，利用计算机寻找数学模式变得越来越重要，因为计算机生成的数据量爆炸式激增。一些非常复杂的数学对象（例如具有数千个维度的对象），可能因为太深奥而无法直接推理。出于这些限制，DeepMind的研究者希望采用人工智能以全新的方式增强数学家的洞察力。

数学家的直觉在数学发现中扮演着极其重要的角色，只有结合严格的形式主义和良好的直觉才能解决复杂的数学问题。下图的框架描述了一种通用方法，数学家可以通过该方法使用机器学习工具来启发他们对复杂数学对象的直觉。这是一种自然且富有成效的方式，将统计学和机器学习很好地融入了数学研究。

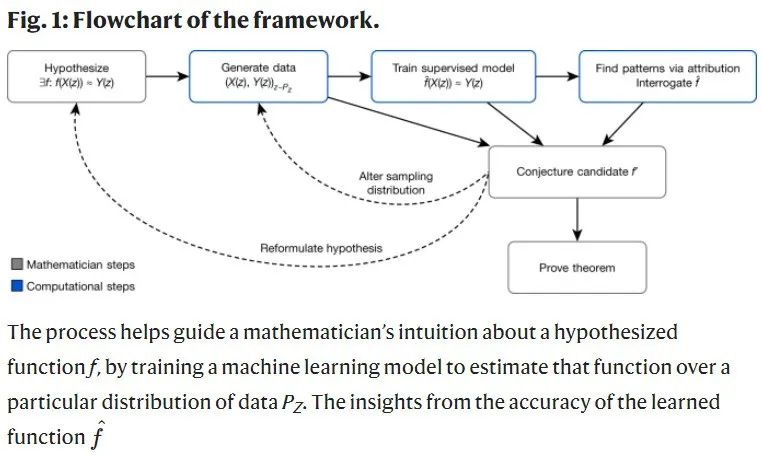
从概念上讲，这个框架提供了一个直觉试验台，可以快速验证两个量之间的关系直觉是否值得研究，如果是，试验台会指导它们之间如何相关。DeepMind已经使用上述框架帮助数学家在两种情况下获得有影响力的数学结果。

DeepMind作为一家全球领先的人工智能公司，他们探索了机器学习 (ML) 在识别数学结构和模式方面的潜力。现在他们帮助数学家解决了一些数学难题，成为AI首次探索纯数学的前沿研究，相关论文今天已在《自然》杂志上发表。

论文地址：

https://www.nature.com/articles/s41586-021-04086-x

具体来说，DeepMind与顶级数学家合作，将AI应用于纯数学中的两个领域：拓扑和表示论。其中DeepMind与牛津大学的 Marc Lackenby 教授和András Juhász 教授一起，通过研究纽结 (Knot)的结构发现了不同数学领域之间的意外联系；与悉尼大学的 Geordie Williamson 教授一起，DeepMind发现了一个关于排列猜想的新公式，该猜想几十年来一直未解决。

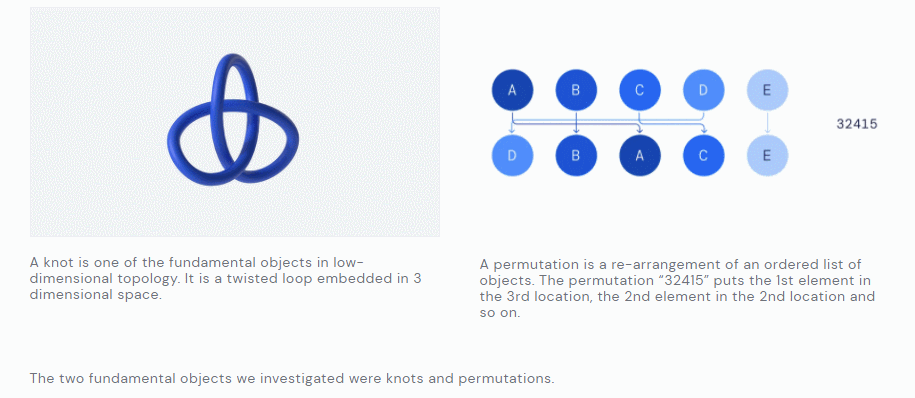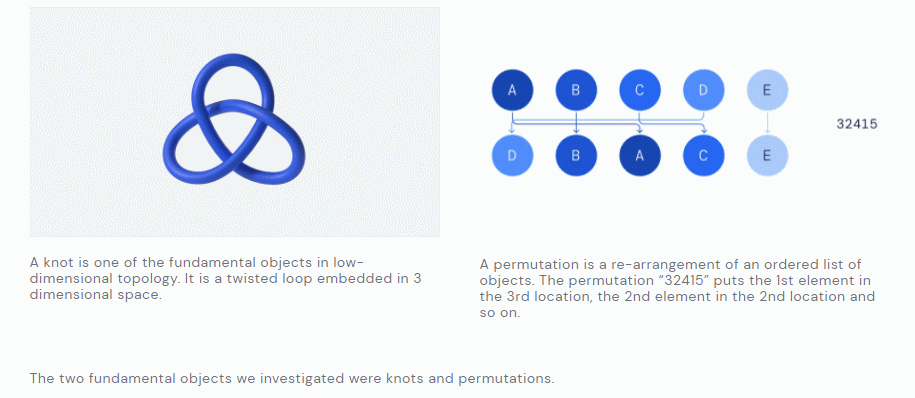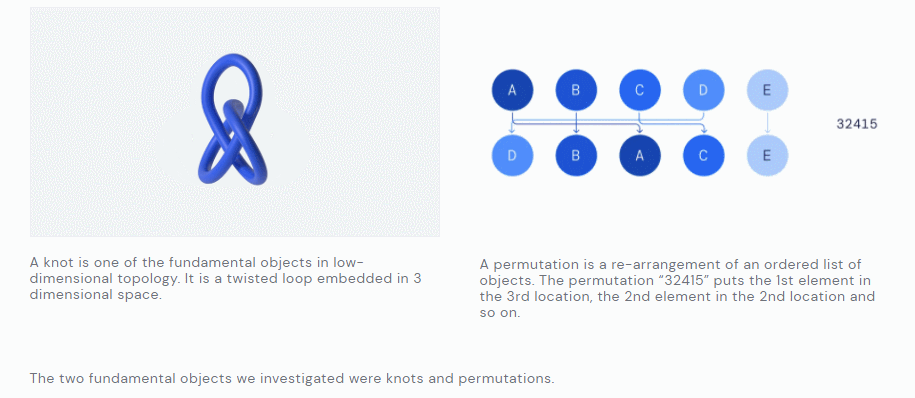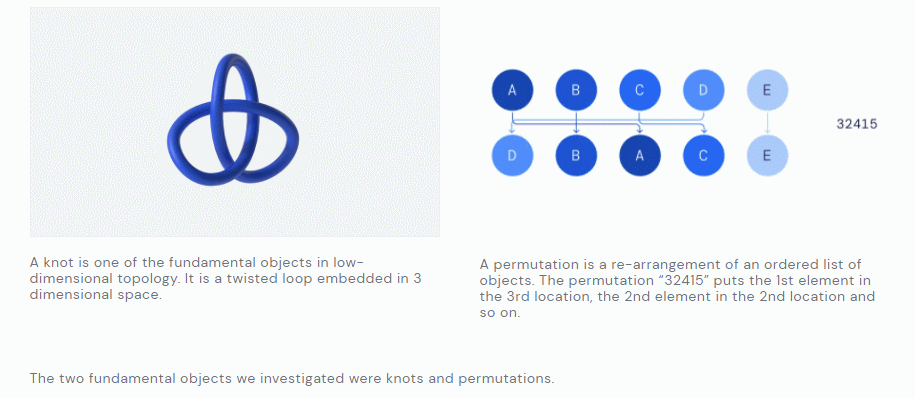
拓扑难题

DeepMind与牛津大学的 Marc Lackenby 教授和András Juhász教授一起，通过研究纽结 (Knot)的结构发现了不同数学领域之间的意外联系。

低维拓扑是数学中一个活跃且有影响力的领域，DeepMind发现了纽结代数和几何不变量之间的关系，建立了数学中一个全新的定理。这些不变量有许多不同的推导方式，但DeepMind主要关注两大类：双曲不变量和代数不变量。这两种类型的不变量来自不同的数学学科，因此在它们之间建立联系是非常有趣的。

下图显示了纽结不变量的一些例子。



DeepMind假设在一个纽结的双曲不变量和代数不变量之间存在一种未被发现的关系。监督学习模型能够检测大量几何不变量和signature σ(K) 之间存在的模式，并用归因技术（attribution technique）确定最相关的特征。下图(a) 显示了cusp几何的三个不变量，图 3b 中部分地显示了其中的关系。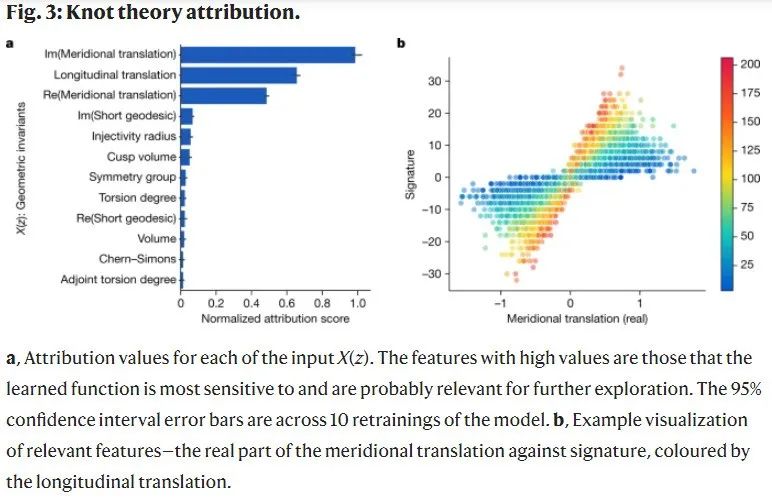

表示论难题

在澳大利亚数学家、悉尼大学教授Geordie Williamson的帮助下，DeepMind借助人工智能解决了表示论中一个长期存在的猜想——组合不变性猜想。

Geordie Williamson

组合不变性猜想指出某些有向图和多项式之间应该存在关系。DeepMind使用机器学习方法确认了这种关系确实存在，并确定其可能与称为破碎的二面角区间（broken dihedral interval）和外反射（extremal reflection）的结构有关。有了这些知识，Williamson教授就能够发现一个令人惊讶的算法来解决组合不变性猜想。

表示论是数学中抽象代数的一支。旨在将代数结构中的元素「表示」成向量空间上的线性变换，借以以研究结构的性质。其中，任何表示都是不可约表示的直和。不可约表示的结构由 Kazhdan-Lusztig (KL) 多项式控制，这些多项式与组合学、代数几何和奇点理论都有着深厚的联系。

组合不变性猜想作为一个关于 KL 多项式的开放猜想，已经存在了约40年，但只有部分进展。在理解对象之间关系方面取得进展的一个障碍是 Bruhat 区间。下图给出了小 Bruhat 区间及其 KL 多项式的例子。



DeepMind的研究把组合不变性猜想作为初始假设，利用机器学习的方法发现了一个能够预测 KL 多项式Bruhat区间的监督学习模型，并且具有相当高的准确率。通过测试将 Bruhat 区间输入网络的方式，研究者发现某些图表和特征的选择特别有助于准确预测。特别地，借助更准确的估计函数，研究者还发现有一种受先前工作启发的子图足以计算 KL 多项式。

该研究已经在超过 300 万个示例中对新算法进行了计算验证，下图是表示论归因的例子。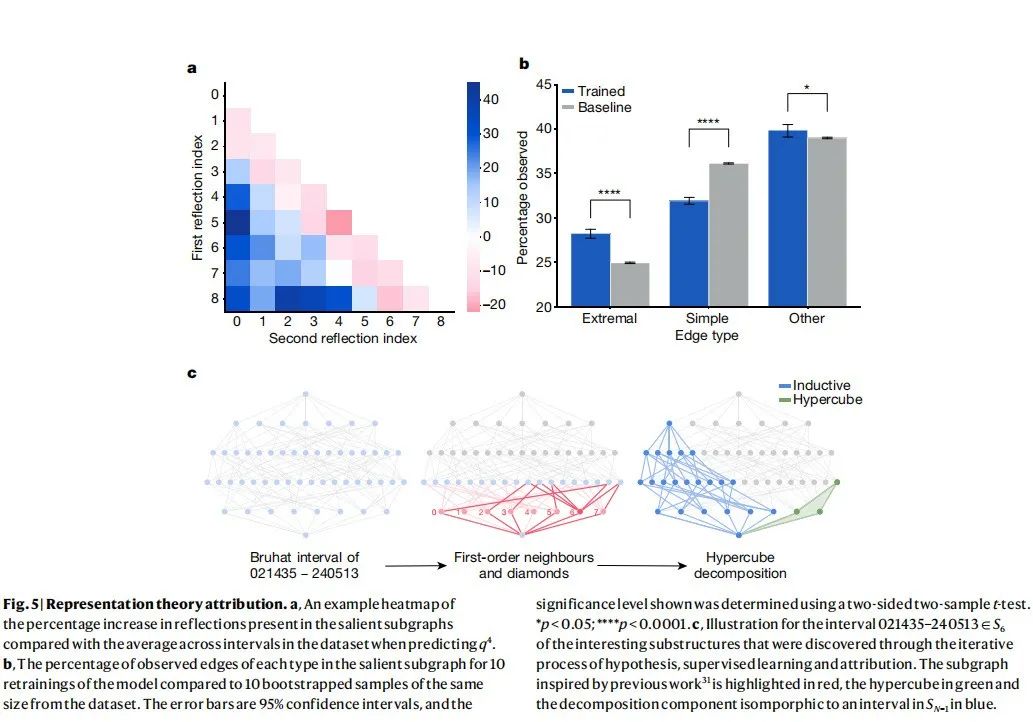



研究者进一步探究了机器学习是否可以阐明不同数学对象之间的关系。下图显示了两个「Bruhat 区间」及其相关的「Kazhdan-Lusztig 多项式」其中，Bruhat 区间是一个图表，它代表了通过一次只交换两个对象来反转对象集合的顺序的所有不同方式。KL 多项式能够告诉数学家一些关于该图在高维空间中存在的不同方式的信息。当 Bruhat 区间有 100 或 1000 个顶点时，有趣的结构才开始出现。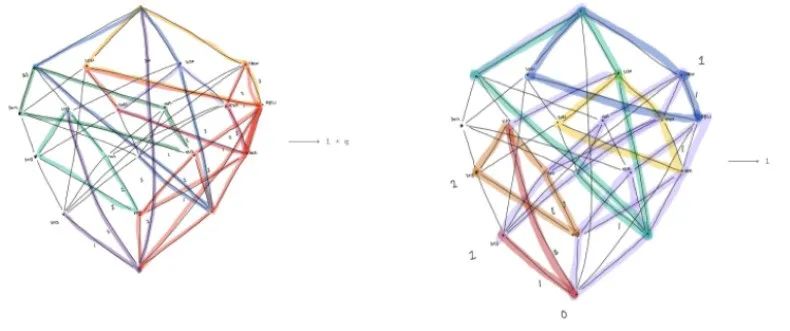

毫无疑问，机器学习和人工智能系统为识别和发现数学模式提供了广阔的前景。DeepMind表示他们希望这项研究成为将人工智能作为纯数学中有用工具的开始。我们相信，那些悬而未决的数学难题，一定会通过数学家与AI的合作突破，人类的直觉也会借助AI上升到一个新的水平。

参考文献：

https://deepmind.com/blog/article/exploring-the-beauty-of-pure-mathematics-in-novel-ways

未来智能实验室的主要工作包括：建立AI智能系统智商评测体系，开展世界人工智能智商评测；开展互联网（城市）大脑研究计划，构建互联网（城市）大脑技术和企业图谱，为提升企业，行业与城市的智能水平服务。每日推荐范围未来科技发展趋势的学习型文章。目前线上平台已收藏上千篇精华前沿科技文章和报告。

  如果您对实验室的研究感兴趣，欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”