OO第四单元——UML及其解析器——总结暨 OO课程大总结

第四单元总结

第四单元主要内容是写代码解析UML，因此需要理解UML

UML相关

starUML的储存方式是一个.mdj文件，通过使用文本编辑器观察这个文件，我们可以看出这是一个json格式储存的文件。

通过把.mdj后缀名改为.json，可以更加直观地观察这个文件。

json

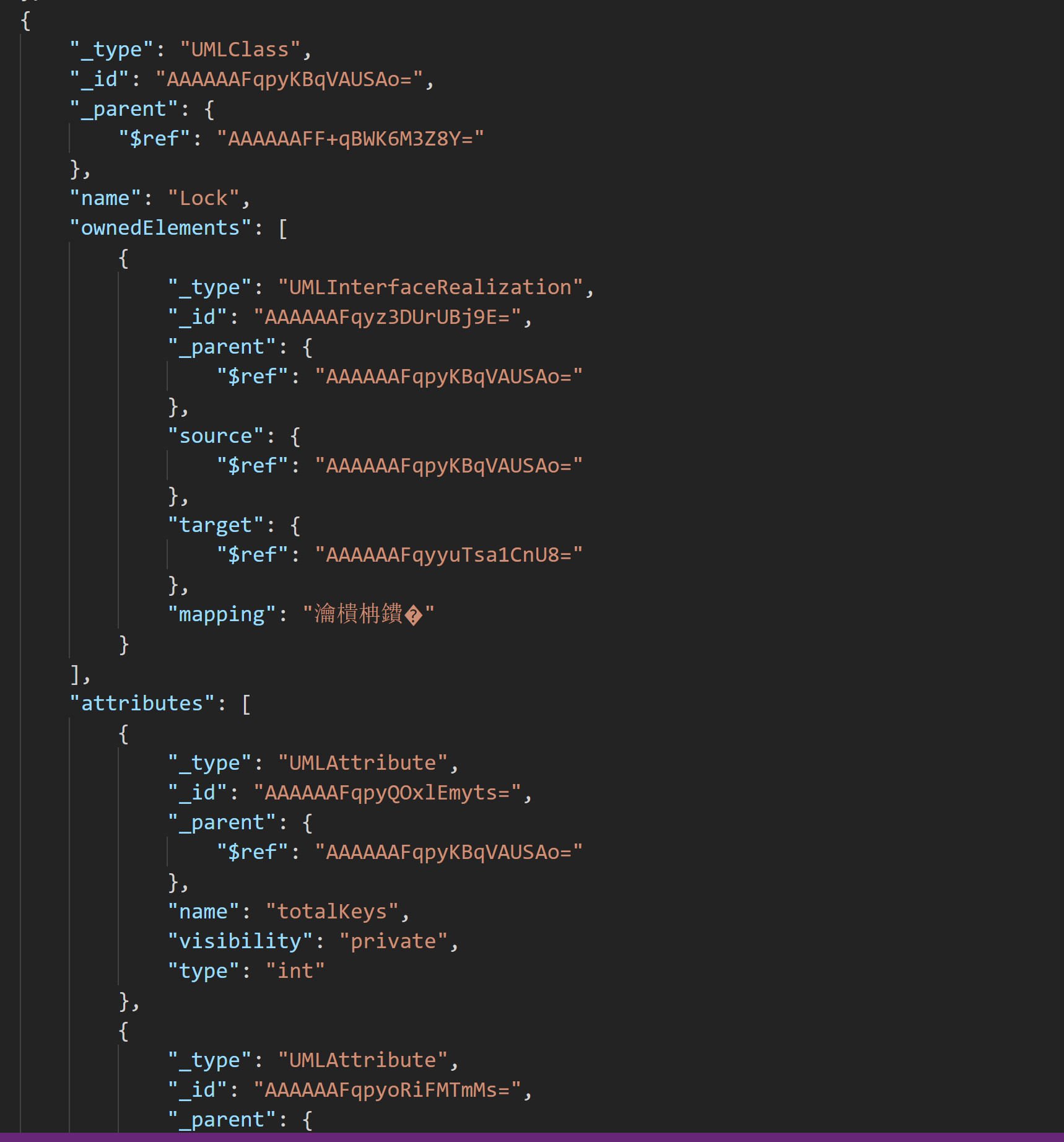
架构分析

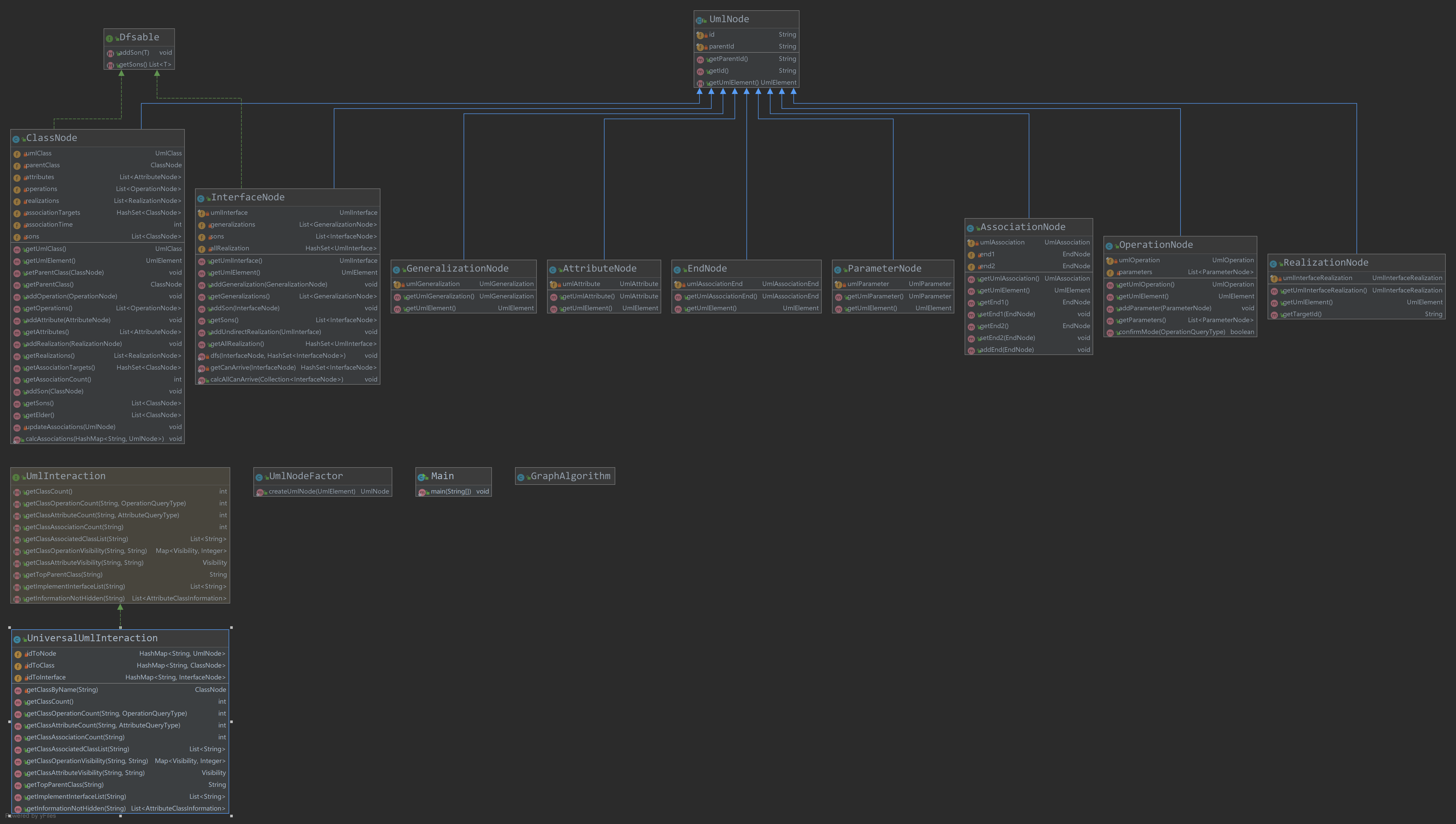
13次类图

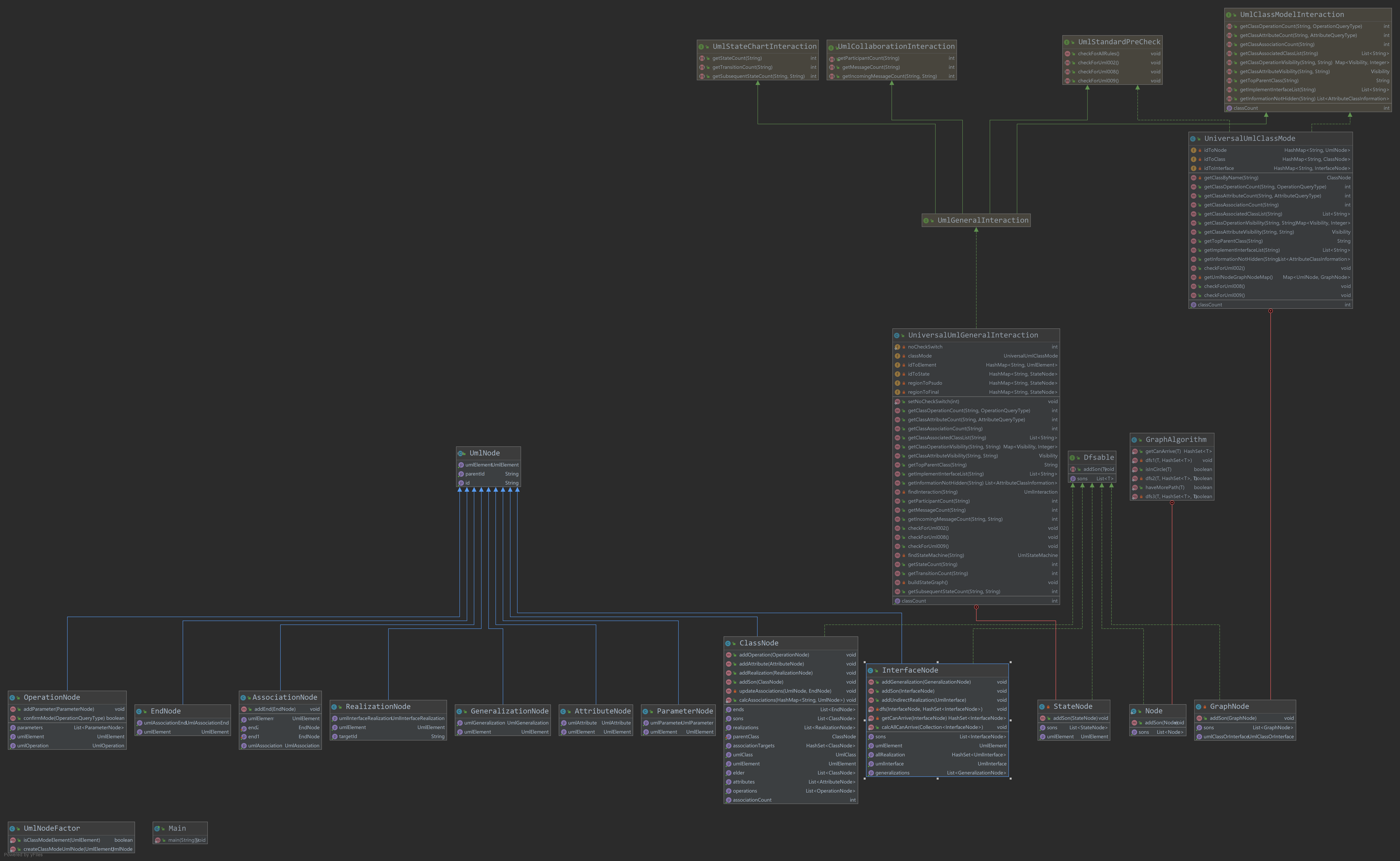
第二次作业类图

以上是我两次作业的类图，我在作业中，给UML中的每一种Element建了一个对应地类。

在建图的时候，我通过各种parent恢复了json文件中的树状结构，便于统计。

关于第二次作业的有效性检查

有效性检查基本上都是图论上的问题。

为了方便/代码复用性/代码美观性，我将图论算法提取出来了。

我新建了一个名为Dfsable的接口。

package graph;import java.util.List;public interface Dfsable<T extends Dfsable<T>> {void addSon(T node);List<T> getSons();
}

以下是图论算法。

package graph;import java.util.ArrayList;
import java.util.HashSet;
import java.util.List;public class GraphAlgorithm {public static class Node implements Dfsable<Node> {private List<Node> sons = new ArrayList<>();@Overridepublic void addSon(Node node) {sons.add(node);}@Overridepublic List<Node> getSons() {return sons;}}/*May not contains itself.*/public static <T extends Dfsable<T>> HashSet<T> getCanArrive(T cur) {HashSet<T> ans = new HashSet<>();dfs1(cur, ans);return ans;}private static <T extends Dfsable<T>> void dfs1(T cur, HashSet<T> ans) {for (T e : cur.getSons()) {if (!ans.contains(e)) {ans.add(e);dfs1(e, ans);}}}public static <T extends Dfsable<T>> boolean isInCircle(T cur) {return dfs2(cur, new HashSet<>(), cur);}private static <T extends Dfsable<T>> boolean dfs2(T cur, HashSet<T> vis,T source) {vis.add(cur);for (T e : cur.getSons()) {if (e.equals(source)) {return true;}if (!vis.contains(e)) {if (dfs2(e, vis, source)) {return true;}}}return false;}public static <T extends Dfsable<T>> boolean haveMorePath(T cur) {return dfs3(cur, new HashSet<>(), cur);}private static <T extends Dfsable<T>> boolean dfs3(T cur, HashSet<T> vis,T source) {vis.add(cur);for (T e : cur.getSons()) {if (vis.contains(e)) {return true;}if (dfs3(e, vis, source)) {return true;}}return false;}
}

通过将所有具有Dfs性质的元素提取出Dfsable接口，我可以只写一次算法，就实现各种搜索。

OO课程总结

OO这门课很快就结束了，在这门课中，我在不断的写代码和学习中理解很多，学会了很多：

架构设计与OO方法

在这一个个单元中，我的架构设计能力和对面向对象的理解有的极大的提高和加深。

第一个单元，我设计的架构一塌糊涂，第二个单元有了起色，第三个单元，我的结构已经基本可以有良好的复用能力的，到了第四个单元，我的架构水平相比第一单元，有了极大的提升。

而对面向对象的理解，我也随着一次次左右有了加深，从一开始只是知道"封装、继承和多态“这些概念，到最后可以熟练甚至下意识地应用这些思想。OO，提高了我的各种能力。

测试理解与实践的演进

在历次作业中，我使用了各种进行脚本测试。

我遇到的主要难点是数据的生成。

其次，另外一个难点是多线程单元的脚本写法。为此，我尝试了解了powershell/linux shell的使用，有了很多的收获。

课程收获

认识的过程，是一个从实践到认识，再从认识到实践的过程。

——马原

OO，一门又爱又”恨“的课。

”恨“当然不是指真的恨，而是说在有时写作业代码感到累的时候，不禁产生的一丝难受。

但是，我也明白，没有难受，就也没有可能有进步和收获。

这也是我爱着OO这门课的原因。

在这门课中，我从一个只写过单文件c语言的工程小白，变成了一个听见了一个宏大任务后不会慌张，可以冷静思考，可以马上开始分析如何”分解这个任务“，”如果是我，我会用什么架构“等人。当然，我肯定与大佬还差的远着呢，或者说，在工程方面依然是一个不折不扣的小白，但是，如果没有OO这门课，我可能至今为止还是写一些简单的“益智”、“好玩”的小程序。

一次又一次的作业、上课、实验和讨论，我逐渐理解、明白了什么是面向对象，为什么要面向对象，如何面向对象......

感谢OO，感谢各位老师、助教和同学。