1. 题目

国际象棋中的骑士可以按下图所示进行移动：

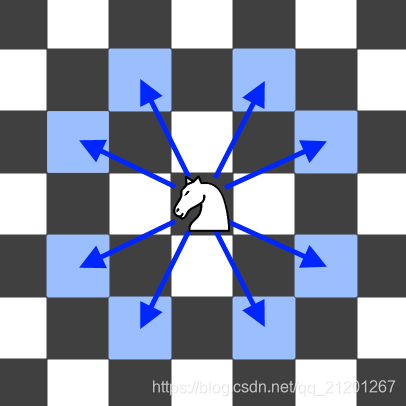
这一次，我们将 “骑士” 放在电话拨号盘的任意数字键（如上图所示）上，
接下来，骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。

每当它落在一个键上（包括骑士的初始位置），都会拨出键所对应的数字，总共按下 N 位数字。

你能用这种方式拨出多少个不同的号码？

因为答案可能很大，所以输出答案模 10^9 + 7。

示例 1：
输入：1
输出：10示例 2：
输入：2
输出：20示例 3：
输入：3
输出：46提示：
1 <= N <= 5000

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/knight-dialer
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

类似题目：
LeetCode 552. 学生出勤记录 II（动态规划）
LeetCode 576. 出界的路径数（动态规划）
LeetCode 688. “马”在棋盘上的概率（DP）

• dp[i][k] 表示在 i键时，剩余k次移动时，产生的号码数量
• 转移：0 可以到 4,6，按照规则来，次数 k-1

class Solution {
public:int knightDialer(int n) {long long dp[10][5001];int mod = 1e9+7;memset(dp, 0, sizeof(dp));dp[0][n-1] = dp[1][n-1] = dp[2][n-1] = dp[3][n-1] = dp[4][n-1]= dp[5][n-1] = dp[6][n-1] = dp[7][n-1] = dp[8][n-1] = dp[9][n-1] = 1;for(int k = n-1; k > 0; k--) {dp[0][k-1] += (dp[4][k]%mod)+(dp[6][k]%mod);dp[1][k-1] += (dp[6][k]%mod)+(dp[8][k]%mod);dp[2][k-1] += (dp[7][k]%mod)+(dp[9][k]%mod);dp[3][k-1] += (dp[4][k]%mod)+(dp[8][k]%mod);dp[4][k-1] += (dp[3][k]%mod)+(dp[0][k]%mod)+(dp[9][k]%mod);// dp[5][k-1] = 0; // 不能转移dp[6][k-1] += (dp[1][k]%mod)+(dp[0][k]%mod)+(dp[7][k]%mod);dp[7][k-1] += (dp[2][k]%mod)+(dp[6][k]%mod);dp[8][k-1] += (dp[1][k]%mod)+(dp[3][k]%mod);dp[9][k-1] += (dp[4][k]%mod)+(dp[2][k]%mod);}int ans = 0;for(int i = 0; i < 10; i++)ans = (ans+dp[i][0])%mod;return ans;}
};

16 ms 6.2 MB

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！