朴素贝叶斯算法-分类算法
1 概率基础
概率定义为一件事情发生的可能性
联合概率:包含多个条件,且所有条件同时成立的概率,记作P(A,B)
条件概率:事件A在另一个事件B已经发生条件下的发送概率,记作P(A|B)
在A1,A2相互独立的情况下,条件概率的特性:P(A1,A2|B)=P(A1|B)P(A2|B)
2 贝叶斯公式
![]()
W:特征向量 C:类别
贝叶斯公式最常用于文本分类,上式左边可以理解为给定一个文本词向量W,那么它属于类别C的概率是多少。式子右边分几部分,P(W∣C)为在给定类别的情况下,该文档的词向量(被预测文档中出现词)的概率,P(C)为每个文档类别的概率(某文档类型词数/总文档词数),P(F1,F2..)预测文档中每个词的概率
可以理解为:![]()
C可以是不同类别
假如有个训练集统计结果如下:
| 特征/统计 | 科技 | 历史 | 汇总 |
| 诸葛亮 | 2 | 60 | 60 |
| 原子弹 | 55 | 20 | 75 |
| 飞机 | 60 | 23 | 83 |
| 卢沟桥事变 | 0 | 65 | 65 |
| 汇总 | 117 | 168 | 285 |
现有一篇被预测文档:出现了原子弹,飞机,卢沟桥事变属于科技、历史的类别概率?
因为P(原子弹,飞机,卢沟桥事变)在每个统计中都是一样的,所有忽略。
P(科技|原子弹,飞机,卢沟桥事变)=P(原子弹,飞机,卢沟桥事变|科技)P(科技)=(2/55)(60/117)(0/117)(117/285)=0
P(历史|原子弹,飞机,卢沟桥事变)=P(原子弹,飞机,卢沟桥事变|历史)P(历史)=(20/168)(23/168)(65/168)(168/285)
上面的例子中,因为某个某个词的出现概率为0导致属于某个类别为0,这是不合理的,所以引入拉普拉斯平滑
3 拉普拉斯平滑
为了避免训练集样本对一些特征的缺失,即某一些特征出现的次数为0,在计算P(X1,X2,X3,...,Xn∣Yi)的时候,各个概率相乘最终结果为零,这样就会影响结果。我们需要对这个概率计算公式做一个平滑处理,即拉普拉斯平滑系数
![]()
其中m为特征词向量的个数,α为平滑系数,当α=1,称为拉普拉斯平滑
4 sklearn朴素贝叶斯实现API
sklearn.naive_bayes.MultinomialNB
sklearn.naive_bayes.MultinomialNB(alpha = 1.0) 朴素贝叶斯分类 alpha:拉普拉斯平滑系数
常用方法:
| 名称 | 解释 |
| fit(X y[,sample_weight]) | 根据X y拟合朴素贝叶斯分类器 |
| get_params(deep=) | 获取此估计器的参数 |
| set_params(PARAMS) | 设置此估计器的参数 |
| partial_fit(X y[,classes,sample_weight]) | 增量拟合一批样本 |
| predict(X) | 对测试向量X组执行分类 |
| predict_log_proda(X) | 返回测试矢量X的对数概率统计 |
| predict_proda(X) | 测试矢量X的返回概率估计 |
| score(X y[,sample_weight]) | 返回给定测试数据和标签的平均精度 |
5 朴素贝叶斯算法案例
sklearn20类新闻分类 ,20个新闻组数据集包含20个主题的18000个新闻组帖子
步骤:①加载20类新闻数据,并进行分割
②生成文章特征词
③朴素贝叶斯estimator流程进行预估
from sklearn.naive_bayes import MultinomialNB
from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics import classification_report
#1加载20类新闻数据,并进行分割
newsgroups = fetch_20newsgroups(subset='all')
#分割
x_train,x_test,y_train,y_test = train_test_split(newsgroups.data,newsgroups.target,test_size=0.25)#2 生成文章特征词,对数据集进行特征抽取
tf = TfidfVectorizer()
#以训练集当中的词的列表进行每篇文章重要性统计
x_train = tf.fit_transform(x_train)
print(tf.get_feature_names())
x_test = tf.transform(x_test)# 进行朴素贝叶斯算法的预测
mlt = MultinomialNB(alpha=1.0)
mlt.fit(x_train,y_train)
y_predict = mlt.predict(x_test)
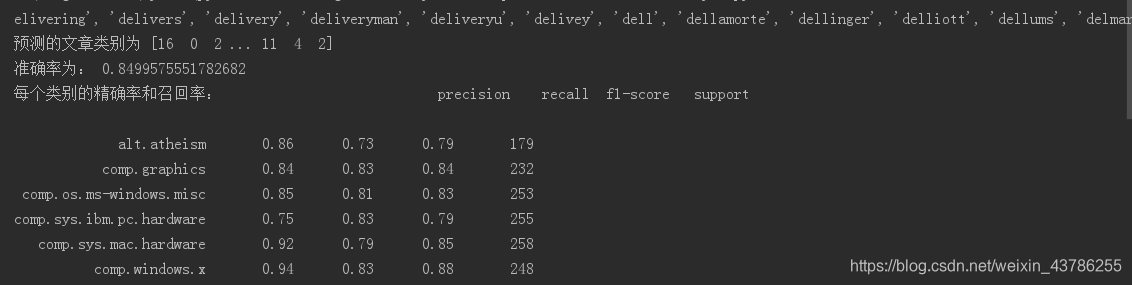
print("预测的文章类别为",y_predict)
score = mlt.score(x_test,y_test)
print("准确率为:", score)
print("每个类别的精确率,召回率和F1:", classification_report(y_test, y_predict, target_names=newsgroups.target_names))
|
6 朴素贝叶斯分类优缺点
优点: ①朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。 ②对缺失数据不太敏感,算法也比较简单,常用于文本分类。 ③分类准确度高,速度快
缺点:需要知道先验概率P(F1,F2,…|C),因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
特点:不需要调参,如果训练集误差大,结果肯定不好。

)



)

![[Java]java反射随笔](http://pic.xiahunao.cn/[Java]java反射随笔)






*)

)
)

