拟合与岭回归

1 什么是过拟合与欠拟合

通过下面两张图来解释过拟合和欠拟合：

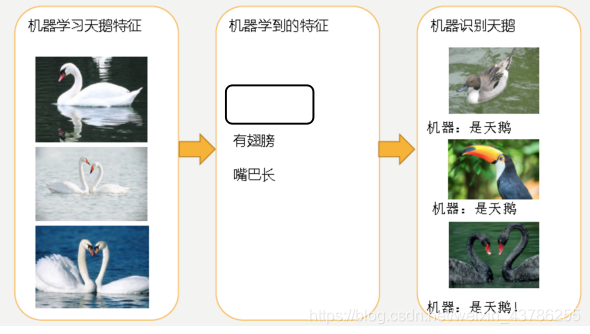
左图中机器通过这些图片来学习天鹅的特征知道了天鹅是有翅膀的，天鹅的嘴巴是长长的。简单的认为有这些特征的都是天鹅。因为机器学习到的天鹅特征太少了，导致区分标准太粗糙，不能准确识别出天鹅。这就是欠拟合

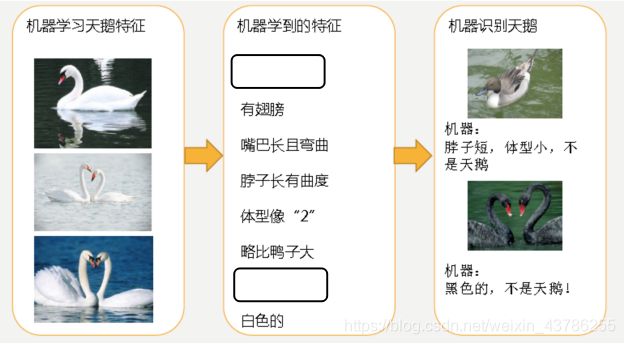
有图中机器通过这些图片来学习天鹅的特征，经过训练后，知道了天鹅是有翅膀的，天鹅的嘴巴是长长的弯曲的，天鹅的脖子是长长的有点曲度，天鹅的整个体型像一个"2"且略大于鸭子。这时候机器已经基本能区别天鹅和其他动物了。但是已有的天鹅图片全是白天鹅的，会认为天鹅的羽毛都是白的，以后看到羽毛是黑的天鹅就会认为那不是天鹅。这就是过拟合

由上图得知欠拟合是训练误差和测试误差都大，过拟合是随着模型的复杂度越来越复杂，训练误差不断减少，决策树就是这样的，但是测试误差先是减少到达某一个临界点后越来越大了，说明过拟合了，只是在训练集合里面考虑训练集的特点，但是测试集里面的特点可能不是这个规律。

过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合，但是在训练数据外的数据集上却不能很好地拟合数据，此时认为这个假设出现了过拟合的现象。(模型过于复杂)。

欠拟合：一个假设在训练数据上不能获得更好的拟合，但是在训练数据外的数据集上也不能很好地拟合数据，此时认为这个假设出现了欠拟合的现象。(模型过于简单)、

2 模型复杂度

线性回归不仅仅只能拟合线性关系数据。现实中大多数数据是非线性关系，对应的就是弯弯曲曲的曲线，求出系数后就变复杂了，因为特征复杂，线性回归非线性也可以去拟合。特征复杂就意味着复杂模型。

假如建立的模型是线性如第一个图，这时候画出来的是一条直线；对于图二的曲线要建立一个模型把这个曲线画出来，那么数据的关系可能是某个平方的值在加上一个值，那模型就变复杂了；有可能还更加复杂的情况，特征更多，数据之间更复杂，某个值的平方加某个值的三次方等。这些x和θ是根据数据来定的，模型复杂的原因：数据的特征值和目标值之间的关系不仅仅是线性关系。

在线性拟合的时候还是求出这些θ参数，不管x是什么东西，当数据比较复杂的时候，θ乘以某个特征，这个时候预测关系比较复杂，因为某些特征是特征平方的关系。你怎么知道这是x的平方还是x的三次方，不用管，因为数据本身就是这种特性，我们的目的是为了求θ。对于线性关系来说，如果数据是复杂，有弯曲关系的时候，容易复杂度变大。

3 鉴别欠拟合与过拟合

欠拟合产生原因：学习到数据的特征过少；解决办法：增加数据的特征数量。

过拟合产生原因：原始特征过多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试数据点；解决办法：进行特征选择，消除关联性大的特征(很难做)，交叉验证(让所有数据都有过训练，不能解决只能验证是哪种拟合)，正则化(了解)。

如何知道是欠拟合还是过拟合呢？一般可以通过交叉验证得来，比较在交叉验证中本身在训练集里面就60%左右的效果，那么说明在训练集训练的时候已经学不到很多东西，就可以认为是欠拟合情况，如果在网格搜索里面把交叉验证单独拿出来发现训练集结果特别好，90%多但是测试集预测的时候发现才80%多，那就认为是过拟合。

总结就是根据训练集结果现象判断，根据交叉验证训练集结果与测试集对比一般是准确率，会看误差，这个有业务去定。

4 过拟合解决方法

特征选择有过滤式（低方差特征）和嵌入式（正则化，决策树，神经网络）。

正则化：如虽然不知道是哪些特征影响，但是可以不断地去试，不断的调整曲线，减少权重，把权重θ3，权重θ4不断减少趋近于0，那么模型就变简单了。所以正则化出发的角度就是在更新权重的过程中，不断的尝试把某一个特征前面的权重θ减小，看下哪个效果好，最终发现有一些特征前面的权重调整到趋近于0的时候效果好，这就是正则化解决问题的角度。

虽然不知道是哪些特征影响，但是可以减少权重，因为权重是我们取求出来的，尽量减少高次项特征的影响

L2正则化：作用：可以使得W的每个元素都很小，都接近于0 ；优点：越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象

线性回归：LinearRegression容易出现过拟合，为了把训练数据集表现更好，把所有训练数据拟合进去。

那么就用L2正则化（Ridge）的方式去解决，Ridge岭回归，带有正则化的回归，能够解决过拟合。

基本上回归解决过拟合的方式就是L2正则化。

回归和分类解决过拟合的方式是不一样的，决策树解决过拟合的方式：①把api里面的叶子节点数量增大；②随机森林。

5 岭回归（Ridge）

岭回归就是带有正则化的回归。

带有正则化的线性回归-Ridge的API：sklearn.linear_model.Ridge

sklearn.linear_model.Ridge(alpha=1.0) 具有l2正则化的线性最小二乘法

alpha:正则化力度（λ也表示正则化力度）

coef_:回归系数

正则化力度对权重有什么影响呢？看下面官网给的一张图

正则化力度越大（右到左），模型越来越简单。所以正则化对权重的影响为：正则化力度越来越大，权重越来越趋近于0。

岭回归进行房价预测如下：

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor,Ridge
from sklearn.metrics import mean_squared_error
# 1获取数据
lb = load_boston()# 2分割数据为训练集合测试集
x_train,x_test,y_train,y_test = train_test_split(lb.data,lb.target,test_size=0.25)# 3进行标准化处理，特征值和目标值都必须进行标准化处理
std1 = StandardScaler()
x_train = std1.fit_transform(x_train)
x_test = std1.transform(x_test)
# 目标值标准化
std2 = StandardScaler()
y_train = std2.fit_transform(y_train.reshape(-1,1))
y_test = std2.transform(y_test.reshape(-1,1))# 4.estimator估计器测试
# 4.3岭回归求解预测
rd = Ridge()
# 输入数据一直不断用训练数据建立模型
rd.fit(x_train,y_train)
print("岭回归系数为",rd.coef_)
# 预测测试集房子价格
y_rdPredict = rd.predict(x_test)
y_rdPredict = std2.inverse_transform(y_rdPredict)
print("sgd测试集每个样本的预测价格：",y_rdPredict)
print("梯度下降均方根误差",mean_squared_error(std2.inverse_transform(y_test),y_rdPredict))

线性回归 LinearRegression与Ridge对比：岭回归：回归得到的回归系数更符合实际，更可靠。另外，能让估计参数的波动范围变小，变的更稳定。在存在病态数据偏多的研究中有较大的实用价值。

6 模型的保存与加载

sklearn的模型保存月加载API：sklearn.externals.joblib

保存：joblib.dump(rf,"test.pkl")

加载：estimator=joblib.load("test.pkl")

注意：文件格式为pkl（二进制文件）

from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression,SGDRegressor,Ridge
from sklearn.metrics import mean_squared_error
from sklearn.externals import joblib
# 1获取数据
lb = load_boston()# 2分割数据为训练集合测试集
x_train,x_test,y_train,y_test = train_test_split(lb.data,lb.target,test_size=0.25)# 3进行标准化处理，特征值和目标值都必须进行标准化处理
std1 = StandardScaler()
x_train = std1.fit_transform(x_train)
x_test = std1.transform(x_test)
# 目标值标准化
std2 = StandardScaler()
y_train = std2.fit_transform(y_train.reshape(-1,1))
y_test = std2.transform(y_test.reshape(-1,1))# 4.estimator估计器测试
# 4.1正规方程求解预测
lr = LinearRegression()
# 输入数据一直不断用训练数据建立模型
lr.fit(x_train,y_train)print("lr回归系数为",lr.coef_)# 保存训练好的模型
joblib.dump(lr,"test.pkl")
y_predict = lr.predict(x_test)
y_predict = std2.inverse_transform(y_predict)
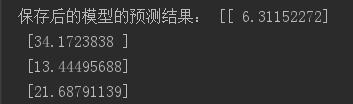
print("未保存模型前的预测结果：",y_predict)# 当时用什么模型训练的这时候就返回什么模型
model = joblib.load("test.pkl")# 预测测试集房子价格
y_modelPredict = model.predict(x_test)
print("保存后的模型的预测结果：",std2.inverse_transform(y_modelPredict))