LeetCode 1727. 重新排列后的最大子矩阵（前缀和+排序）

文章目录

- 1. 题目
- 2. 解题

1. 题目

给你一个二进制矩阵 matrix ，它的大小为 m x n ，你可以将 matrix 中的列按任意顺序重新排列。

请你返回最优方案下将 matrix 重新排列后，全是 1 的子矩阵面积。

示例 1：

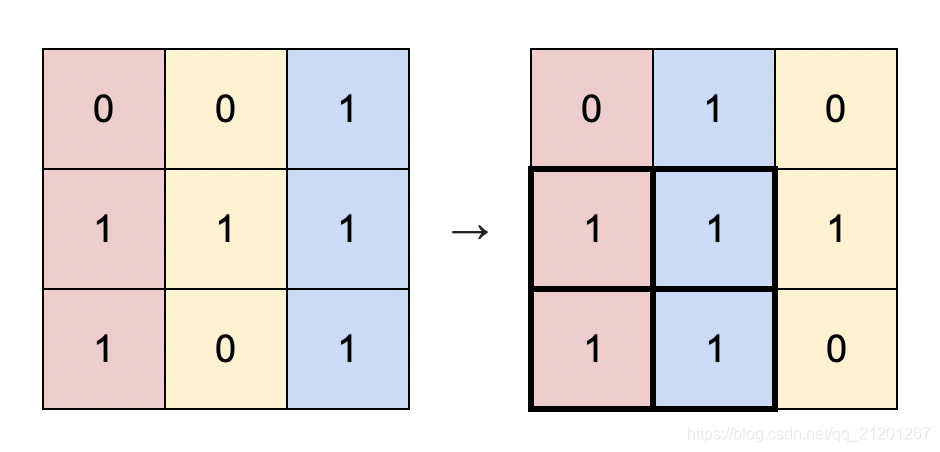
输入：matrix = [[0,0,1],[1,1,1],[1,0,1]]
输出：4
解释：你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分，面积为 4 。

示例 2：

输入：matrix = [[1,0,1,0,1]]
输出：3
解释：你可以按照上图方式重新排列矩阵的每一列。
最大的全 1 子矩阵是上图中加粗的部分，面积为 3 。示例 3：
输入：matrix = [[1,1,0],[1,0,1]]
输出：2
解释：由于你只能整列整列重新排布，
所以没有比面积为 2 更大的全 1 子矩形。示例 4：
输入：matrix = [[0,0],[0,0]]
输出：0
解释：由于矩阵中没有 1 ，
没有任何全 1 的子矩阵，所以面积为 0 。提示：
m == matrix.length
n == matrix[i].length
1 <= m * n <= 10^5
matrix[i][j] 要么是 0 ，要么是 1 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/largest-submatrix-with-rearrangements
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

类似题目：
LeetCode 1277. 统计全为 1 的正方形子矩阵（DP）
LeetCode 1504. 统计全 1 子矩形（记录左侧的连续1的个数）

计算列的前缀和
将每行为底边，且高度不为0的列排序，计算最大矩形面积

class Solution {
public:int largestSubmatrix(vector<vector<int>>& matrix) {int m = matrix.size(), n = matrix[0].size();vector<vector<int>> h(matrix);int area = 0;for(int i = 0; i < m; i++){vector<int> height;for(int j = 0; j < n; j++){if(matrix[i][j] == 0)h[i][j] = 0;elseh[i][j] += i > 0 ? h[i-1][j] : 0;//前缀和if(h[i][j] > 0)height.push_back(h[i][j]);}sort(height.begin(), height.end());//排序int width = height.size();//宽度for(int k = 0; k < width; k++){area = max(area, height[k]*(width-k));}					// 当前高 * 剩余宽度}return area;}
};