电磁波,又称电磁辐射,是由同相振荡且互相垂直的电场与磁场在空间中以波的形式传递能量和动量,其传播方向垂直于电场与磁场构成的平面。电磁辐射的载体为光子,不需要依靠介质传播,在真空中的传播速度为光速。电磁辐射可按照频率分类,从低频率到高频率,主要包括无线电波、微波、红外线、可见光、紫外线、X射线和伽马射线。人眼可接收到的电磁辐射,波长大约在380至780纳米之间,称为可见光。只要是本身温度大于绝对零度的物体,都可以发射电磁辐射,而世界上并不存在温度等于或低于绝对零度的物体。因此,人们周边所有的物体时刻都在进行电磁辐射。尽管如此,只有处于可见光频域以内的电磁波,才可以被人们肉眼看到。
目录
[隐藏]- 1 历史
- 2 概念
- 2.1 波动模型
- 2.2 粒子模型
- 2.3 传播速度
- 3 热辐射
- 4 电磁波谱
- 5 导引
- 6 参见
- 7 参考文献
- 8 外部链接
历史[编辑]

电磁波首先由詹姆斯·麦克斯韦于1865年预测出来,而后由德国物理学家海因里希·赫兹于1887年至1888年间在实验中证实存在。麦克斯韦推导出电磁波方程,一种波动方程,这清楚地显示出电场和磁场的波动本质。因为电磁波方程预测的电磁波速度与光速的测量值相等,麦克斯韦推论光波也是电磁波[1]。
概念[编辑]


电动力学专门研究电磁波的物理行为,是电磁学的分支。在电动力学里,根据麦克斯韦方程组,随着时间变化的电场产生了磁场,反之亦然。因此,一个振荡中的电场会产生振荡的磁场,而一个振荡中的磁场又会产生振荡的电场,这样子,这些连续不断同相振荡的电场和磁场共同地形成了电磁波。
电场,磁场都遵守叠加原理。因为电场和磁场都是矢量场,所有的电场矢量和磁场矢量都适合做矢量加运算。例如,一个行进电磁波,入射于一个介质,会引起介质内的电子振荡,因而使得它们自己也发射电磁波。这会与入射波发生干涉,因而造成折射或衍射等等现象。
在非线性介质内(例如,某些晶体),电磁波会与电场或磁场产生相互作用,这包括法拉第效应[2][3]和克尔效应[4]。
当电磁波从一种介质入射于另一种介质时,假若两种介质的折射率不相等,则会产生折射现象,电磁波的方向和速度会改变。斯涅尔定律专门描述折射的物理行为。
假设,由很多不同频率的电磁波组成的光波,从空气入射于棱镜。而因为菱镜内的材料的折射率跟电磁波的频率有关,会产生色散现象:光波会色散成一组可观察到的电磁波谱。
量子电动力学是描述电磁辐射与物质之间的相互作用的量子理论。电磁波不但会展示出波动性质,电磁波也会展示出粒子性质(参阅波粒二象性)。这些性质已经在很多物理实验中证实。当用比较大的时间尺度和距离尺度来测量电磁辐射时,波动性质会比较显著;而用比较小的时间尺度和距离尺度,则粒子性质比较显著。
有时候,波动性质和粒子性质会出现于同一个实验,例如,在双缝实验里,当单独光子被发射于两条细缝时,单独光子会穿过这两条细缝,自己与自己干涉,就好像波动运动一样。可是,它只会被光电倍增管侦测到一次。当单独光子被发射于迈克耳孙干涉仪或其它种干涉仪时,也会观测到类似的自我干涉现象。
波动模型[编辑]
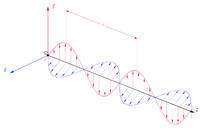
描述光波的一个很重要的物理参数是频率。一个波的频率是它的振荡率,国际单位制单位是赫兹。每秒钟振荡一次的频率是一赫兹。
波是由很多前后相继的波峰和波谷所组成,两个相邻的波峰或波谷之间的距离称为波长。电磁波的波长有很多不同的尺寸,从非常长的无线电波(有一个足球场那么长)到非常短的伽马射线(比原子半径还短)。
频率与波长成反比:
 ;
;
其中,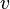 是波速(在真空里是光速;在其它介质里,小于光速),
是波速(在真空里是光速;在其它介质里,小于光速), 是频率,
是频率, 是波长。
是波长。
当波从一个介质透射至另一个介质时,波速会改变,但是频率不变。
干涉是两个或两个以上的波,叠加形成新的波样式。假若几个电磁波的电场同方向,磁场也同方向,则这干涉是建设性干涉;反之,则是摧毁性干涉。
电磁波的能量,又称为辐射能。这能量,一半储存于电场,另一半储存于磁场。用方程表达[5]:
 ;
;
其中,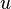 是单位体积的能量,
是单位体积的能量,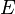 是电场数值大小,
是电场数值大小, 是磁场数值大小,
是磁场数值大小, 是电常数,
是电常数,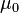 是磁常数。
是磁常数。
粒子模型[编辑]
电磁辐射拥有像粒子的性质。电磁辐射是由离散能量的波包形成的,这波包又称为量子,或光子。光子的能量与电磁辐射的频率成正比。由于光子可以被带电粒子吸收或发射,光子承担了一个重要的角色:能量的传输者。根据普朗克关系式,光子的能量是
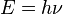 ;
;
其中,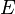 是能量,
是能量, 是普朗克常数,
是普朗克常数, 是频率。
是频率。
这光子能量方程乃是更广义的电磁振子一个特别案例。在低温状况,电磁振子的平均能量与能量均分定理的预测相差很大。这显示出,由于量子效应,能量均分在低温状况是不正确的[6]。
当一个光子被原子吸收的同时,也会激发它的束缚电子,将电子的能级升高。假若光子给出的能量足够大,电子可能会逃离原子核的束缚吸引,成为自由电子。这程序称为光离化(photoionization)。逆反过来,一个跃迁至较低能级的电子,会发射一个能量等于能级差额的光子。由于原子内的电子能级是离散的,每一种原子只能发射和吸收它的特征频率的光子[7]。
综合在一起,这些效应解释了光波的吸收光谱。在介质内的原子,因为吸收不同频率的光波,造成了光谱的暗线。光波所通过的介质的组成成分,决定了吸收光谱的表征。举例而言,一个遥远的恒星的光谱,其暗线与恒星的大气尘的原子组合有关.这些暗线对应于原子的容许能级。类似的现象也会发生于光波的发射.当电子从高能级量子态跃迁至低能级量子态的同时,光波也会被发射出来,其能量等于两个能级的差值。这现象显现于星云的发射光谱。今天,科学家用这现象来观测恒星的内部结构.这现象的红移被用来计算恒星离地球的距离。
传播速度[编辑]
呈加速运动的电荷或随着时间而变化的电磁场,会产生电磁辐射。在自由空间里,电磁辐射以光速传播。准确的计算其物理行为必须引用推迟时间的概念。这会增加电场和磁场的表达式的复杂程度(参阅杰斐缅柯方程)。这些多加的项目详细地描述电磁辐射的物理行为。当任意一根导线(或别种导电体,像天线)传导交流电的时候,同频率的电磁辐射也会被发射出来[8]。
在量子层次面,当带电粒子的波包振荡或加速时,会产生电磁辐射带电粒子的量子态可以用几个本征量子态的含时形式的叠加来表达(请参阅双态系统)。当系统处于稳定状态时,由于含时形式会被其复共轭删除,带电粒子处于每一个本征量子态的概率是常数。但是,当系统被微扰时(例如,外电场被开启),概率变为跟时间有关。带电粒子处于某本征量子态的概率会随时间而变化。这样,带电粒子会从某个本征量子态跃迁至另外一个本征量子态,因而产生电磁辐射[7]。
依状况的不同,电磁辐射的物理行为,可能像波动,又可能像粒子。从波动角度,电磁辐射的主要物理特征是速度、波长、频率。从粒子角度,电磁辐射是由一群称为光子的粒子组成。每一个光子的能量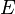 与波动的频率
与波动的频率 的关系则是由普朗克关系式给出:
的关系则是由普朗克关系式给出:
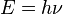 ;
;
其中, 是普朗克常数。
是普朗克常数。
不论是粒子还是波动,电磁辐射必然遵守一条定则:不管观察者的速度有多快或多慢,相对于观察者,电磁波永远以光速传播于真空。这明智的洞察引导爱因斯坦发展出狭义相对论,成为狭义相对论的第二条基本原理。
在其它不同于真空的介质内,电磁波传播的速度会小于光速。一个介质的折射率 是光速
是光速 与电磁波传播于介质的速度
与电磁波传播于介质的速度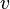 的比例:
的比例:
 。
。
热辐射[编辑]
物质的基本结构,是由一群带电粒子,以各种不同的方式结合组成。当电磁波入射于物质时,会造成物质的带电粒子的振荡和能量增加。这些能量最终的命运依状况而定。它们很可能会立刻被重新辐射,成为反射辐射或透射辐射。它们也很可能会消散成为物质内的其它微观运动,达成热平衡后,再转以热能的形式出现。除了少数像荧光、非线性光学效应(nonlinear optical effect)、光化学反应(photochemical reaction) 和光生伏打效应(photovoltaic effect)等等例子以外,被吸收的电磁波大多会直接地存入其能量,因而将物质加热。对于红外辐射和非红外辐射,都会发生这样的物理行为。强烈的无线电波能够热灼伤活生生的细胞组织,也能够煮熟食物。红外线激光,足够强烈的可见光激光和紫外线激光,都可以很容易地点燃纸张。离子化电磁波可以使得物质内的电子拥有高动能,因而破坏其化学键。但是在电子与其它原子碰撞多次后,最终大部分的能量会转换为热能。这整个程序只需短短的几分之一秒。很多人士都认为,红外线波是热的一种形式,而其它电磁波不是.这是一个错误的物理概念。任何被吸收的电磁波都可以使物质加热。
吸收辐射的逆反程序是热辐射。在物质内部大部分的热能都归功于带电粒子的随机运动。这能量可以从物质内被辐射出。形成的辐射可能后来又被另外一个物质吸收。存入的能量会使物质加热。热辐射是热传输的一个很重要的机制。
在一个不透明的空腔内,在热平衡状况,电磁波可以等效地视为热能的一种形式,拥有最大的辐射熵。就像物质一样,电磁波的热力势也是良好定义的。空腔内的热辐射的能量密度(参阅普朗克定律)是
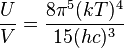 ;
;
其中, 是空腔中电磁场的总能量,
是空腔中电磁场的总能量,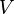 是空腔的体积,
是空腔的体积, 是玻尔兹曼常量,
是玻尔兹曼常量,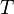 是空腔内部温度,
是空腔内部温度, 是光速。
是光速。
取对于温度的导数,电磁场的有效比热容量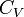 是
是
 。
。
电磁波谱[编辑]

γ = 伽马射线
X射线:
HX = 硬X射线
SX = 软X射线
紫外线:
EUV = 极端紫外线
NUV = 近紫外线
红外线:
NIR = 近红外线
MIR =中红外线
FIR = 远红外线
微波:
EHF = 极高频
SHF = 超高频
UHF = 特高频
无线电波:
VHF = 甚高频
HF = 高频
MF = 中频
LF = 低频
VLF = 甚低频
ULF = 特低频
ELF = 极低频
按照波长长短,从长波开始,电磁波可以分类为无线电波、微波、红外线、可见光、紫外线、X-射线和伽马射线等等。普通实验使用的光谱仪就足以分析从2 纳米到2500 纳米波长的电磁波。使用这种仪器,可以得知物体、气体或甚至恒星的详细物理性质。这是天文物理学的必备仪器。例如,因为超精细分裂,氢原子会发射波长为21.12厘米的无线电波[9]。
人类眼睛可以观测到波长大约在400 纳米和700 纳米之间的电磁辐射,称为可见光。
每一种电极性分子,会对应着某些特定频率的微波,使得电极性分子随着振荡电场一起旋转,这机制称为电介质加热(dielectric heating)。由于这种机制(不是热传导机制),电极性分子会吸收微波的能量。微波炉就是应用这运作原理,通过水分子或脂肪的旋转,更均匀地将食物加热,减少等候时间。
导引[编辑]
麦克斯韦方程组可以描述电磁波的普遍物理现象。在自由空间里,源项目等于零(源电荷等于零,源电流等于零)。除了没有任何事发生的解答以外(电场和磁场都等于零),方程仍旧允许不简单的解答,电场和磁场随着时间和位置变化[8]。采用国际单位制,处于自由空间状况的麦克斯韦方程组表达为
 、(1)
、(1) 、(2)
、(2)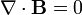 、(3)
、(3) ;(4)
;(4)
其中, 是电场,
是电场, 是磁场,
是磁场, 是真空电容率,
是真空电容率,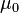 是真空磁导率。
是真空磁导率。
满足上述条件的一个解答是 ,然而这是一个平庸解,并没有什么有意思的物理意义。若想得到有意思的解答,必须稍做一些运算。取公式 (2)的旋度,
,然而这是一个平庸解,并没有什么有意思的物理意义。若想得到有意思的解答,必须稍做一些运算。取公式 (2)的旋度,
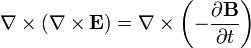 。(5)
。(5)
应用一个矢量恒等式,再将公式 (1)代入,则可得到:
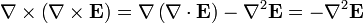 。(6)
。(6)
应用公式 (4),公式 (5)右边变为
 。(7)
。(7)
将公式 (6)和 (7)代回公式 (5),可以得到电场的波动方程:
-
 。
。
使用类似的方法,可以得到磁场的波动方程:
-
 。
。
这两个方程就是真空的电磁波方程,描述传播于真空的电磁波。更简易地表达,
 、
、 ;
;
其中,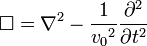 是达朗白算符,
是达朗白算符, 是波动传播的速度。
是波动传播的速度。
在自由空间里,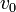 是光速
是光速 。麦克斯韦方程组连结了三个基本物理量:真空电容率
。麦克斯韦方程组连结了三个基本物理量:真空电容率 、真空磁导率
、真空磁导率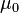 和光速
和光速 。在这导引以前,物理界并不知道,在光波,电场和磁场之间,有那么紧密的关系。
。在这导引以前,物理界并不知道,在光波,电场和磁场之间,有那么紧密的关系。
前面已经找到了两个方程。但是麦克斯韦方程组有四个方程,所以,隐藏在这方程里,还有很多重要的讯息。思考一个一般的电场矢量波动解答,
 ;
;
其中,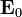 是常数振幅,
是常数振幅, 是任意二次可微函数,
是任意二次可微函数, 是波矢量,
是波矢量, 是位置矢量,
是位置矢量, 是角频率。
是角频率。
波动方程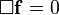 的一般性解答是
的一般性解答是 。也就是说,
。也就是说,
 。
。
将电场的公式代入公式 (1):
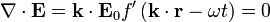 。
。
只要电场垂直于波矢量(波动传播的方向),这函数形式的电场必定满足麦克斯韦方程组:
 。
。
再将电场的公式代入公式 (2):
 。
。
所以,电场与其对应磁场的关系为:
 。
。
在自由空间内,电磁波不只是有以光速传播的性质,电磁波的电场部分和磁场部分有特定的相对定向、相对大小。它们之间的相位一样。电场,磁场,波动传播的方向,都互相垂直于对方。波动传播的方向是 。
。
从电磁波传播的方向看去,电场或许是以上下的方式震荡,而磁场以左右的方式震荡。但若将这图样旋转90度,则电场以左右的方式震荡,而磁场以上下的方式震荡,而波动传播的方向仍旧相同。这是波动方程的另一种解答。对于波动同样传播的方向,这定向的任意性现象称为偏振[8]。

)
之异象解析和自我实现。...)

)

)






)

)


)

