
线性回归模型属于经典的统计学模型,该模型的应用场景是根据已知的变量(自变量)来预测某个连续的数值变量(因变量)。例如,餐厅根据每天的营业数据(包括菜谱价格、就餐人数、预定人数、特价菜折扣等)预测就餐规模或营业额;网站根据访问的历史数据(包括新用户的注册量、老用户分活跃度、网页内容的更新频率等)预测用户的支付转化率。
在开始多元线性模型前介绍下一元线性模型。数学公式可以表示为:
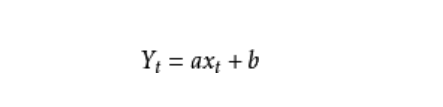
一个因变量,一个自变量。参数求解公式为:
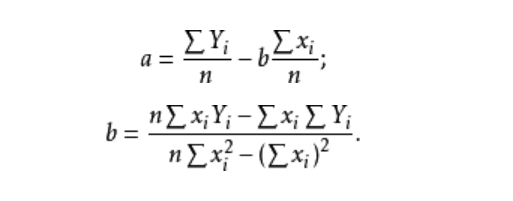
多元线性回归模型与一元线性回归模型的区别就是,自变量的增加。其数学表达式为:
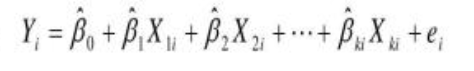
可以简写为:
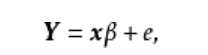
β代表多元线性回归模型的偏回归系数,e代表了模型拟合后每一个样本的误差项。利用最小二乘法求解β,可以得到:
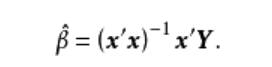
将相应的x值,y值代入公式即可求得β。
我们构建模型的目的是为了预测,即根据已知的自变量X值预测未知的因变量y的值。本文是利用Python 实现这一目标。
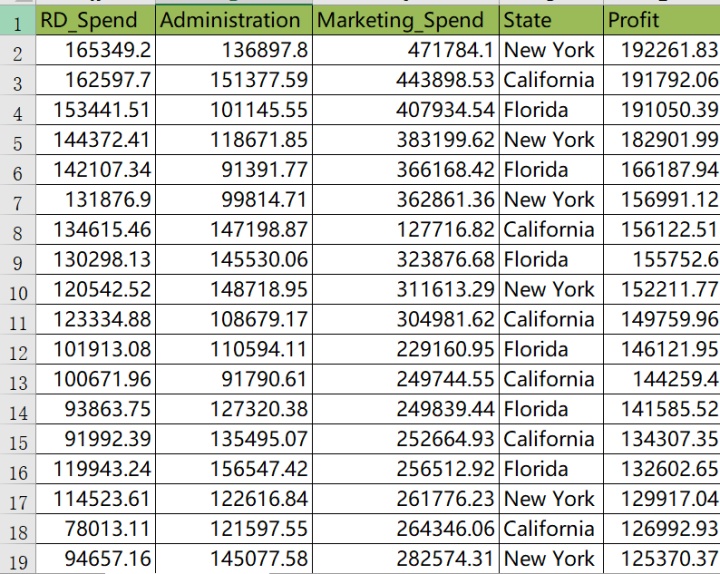
这里以某产品的利润数据集为例,该数据集包含5个变量,分别是产品的研发成本、管理成本、市场营销成本、销售市场和销售利润。其中销售利润Profit为因变量,其他变量为自变量。
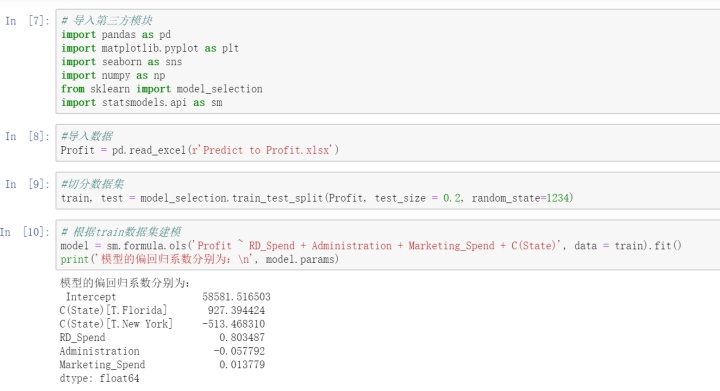
回归模型的建模和预测
将导入数据的数据进行切割,训练集用来训练模型,测试集用来预测。
测试集删除因变量Profit,剩下的自变量进行预测,结果用来跟删除的因变量进行对比,比较模型的预测能力。
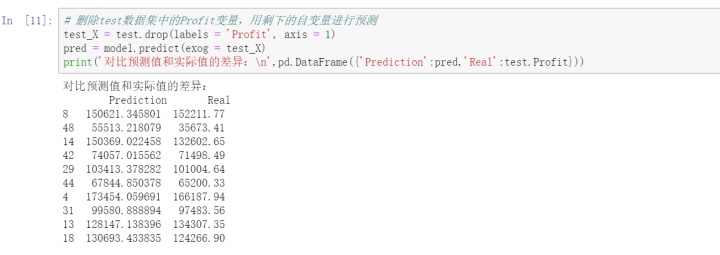
数据集中的State变量为字符型的离散变量,需要进行哑变量处理。将State套在C()中,表示将其当作分类(Category)变量处理。以上默认State(California)为对照组。
接下来通过pandas中的get_dummies函数生成哑变量,以New York作为对照组。
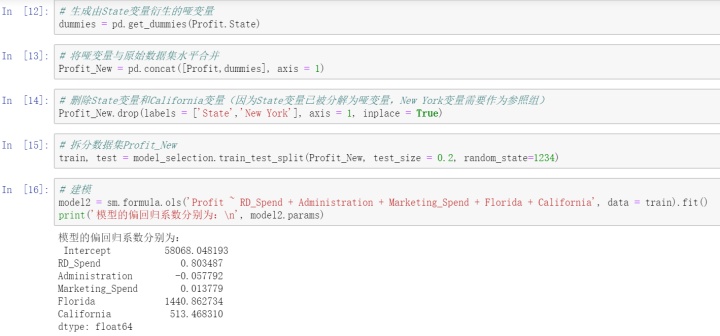
如上结果所示,从离散变量State中衍生出来的哑变量在回归系数的结果里只保留了Florida和California,而New York作为了参照组。得到的结果表示该模型公式为:
Profit=58068.05+0.80RD_Spend-0.06Administation+0.01Marketing_Spend+1440.86Florida+513.47California
如何解释该模型呢,以RD_Spend和Florida为例,在其他变量不变的情况下,研发成本每增加2美元,利润会增加0.80美元;在其他变量不变的情况下,以New York为基准线,如果在Florida销售产品,利润会增加1440.86美元。
虽然模型已经建成,但是模型的好坏还需要模型的显著性检验和回归系数的显著性检验。
回归模型的假设检验
模型的显著性检验使用F检验。
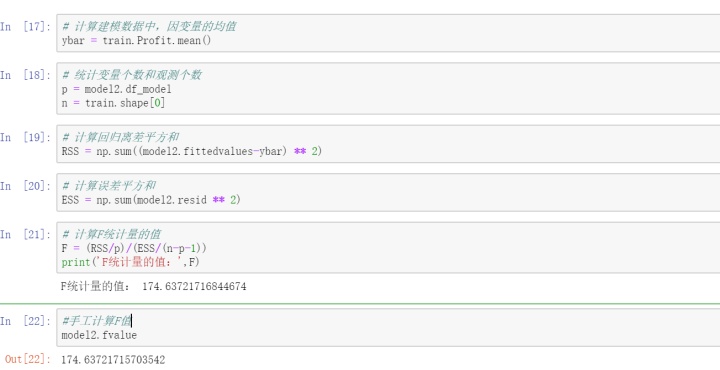
手工计算F值和模型自带的F统计值计算完全一致。,接下俩将计算得出的F统计值和理论F分布的值进行比较。

计算出的F统计值远远大于理论F值,这里可以拒绝原假设,即认为多元线性回归是显著的,也就是回归模型的偏回归系数不全为0。
回归系数的显著性检验t检验
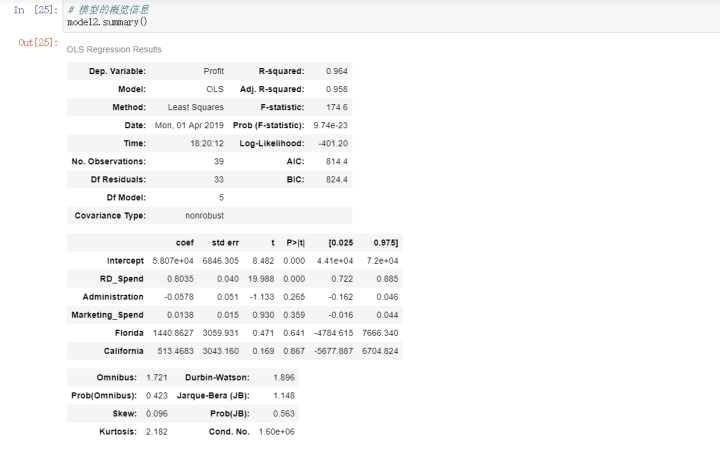
如上结果所示,模型的概览信息包含三个部分,第一部分主要是有关模型的信息,例如模型的判决系数R2,用来衡量自变量对因变量的解释程度,模型的F统计值,用来检验模型的显著性;第二部分主要包含偏回归系数的信息,例如回归系数的Coef、t统计量值、回归系数的置信区间等;第三部分主要涉及模型的误差项e的有关信息。
在第二部分的内容中,含有每个偏回归系数的t统计量值,它的计算就是由估计值coef和标准差std err的商所得的,同时也有t统计量值对应的概率值p,用来判别统计量是否显著的直接办法,通常概率值p小于0.05时表示拒绝原假设。从返回的结果可知,只有截距项Intercept和研发成本RD_Spend对应的值小于0.05,才说明其余变量都没有通过系数的显著性检验,即在模型中这些变量不是影响利润的重要因素。
回归模型的诊断
当回归模型建好之后,并不意味着建模过程的结束,还需要进一步对模型进行诊断。由统计学知识可知,线性回归模型需要满足一些假设前提,只有满足了这些假设,模型才是合理的。需满足:误差e服从正态分布,无多重共线性,线性相关性,误差项e的独立性,方差齐性。
正态性检验,由y=Xβ+e来说,等式右边的自变量属于已知变量,而等式左边的因变量服从正态分布,要求残差项要求正态分布,但其实质就是要求因变量服从正态分布。关于正态性检验通常运用两类方法,分别是定性的图形法(直方图、PP图或QQ图)和定量的非参数法(Shapiro检验和K-S检验),以下是直方图法,
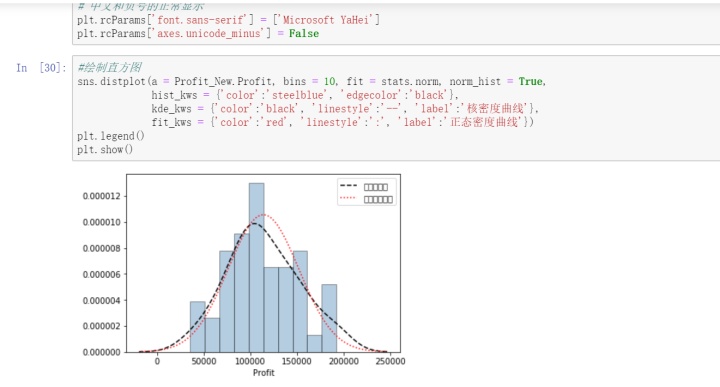
从图中看,和密度曲线和正态分布密度曲线的趋势比较吻合,故直观上可以认为利润变量服从正态分布。以下是PP图和QQ图法,

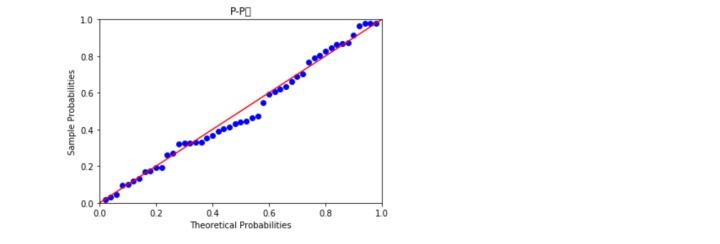
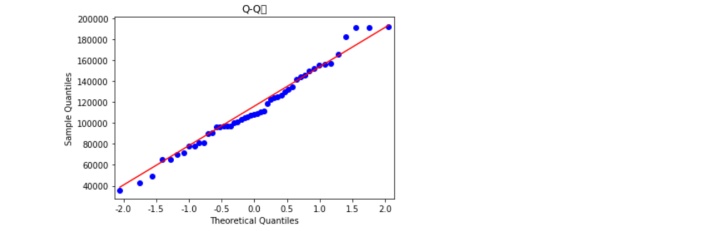
PP图思想是对比正态分布的累计概率值和实际分布的累计概率值,而QQ图则比正态分布的分位数和实际分布的分位数。判断变量是否近似服从正态分布的标准是:如果散点都比较均匀地散落在直线上,就说明近似服从正态分布,否则就认为数据不服从正态分布。如图所知,不管是PP图还是QQ图,绘制的散点均落在直线的附近,没有较大的偏离,故认为利润变量近似服从正态分布。
多重共线性检验
多重共线性是指模型中的自变量之间存在较高的线性相关关系,它的存在给模型带来严重的后果。可以使用方差膨胀因子VIF来鉴定,如果VIF大于10,则说明变量间存在多重共线性;如果如果VIF大于100,则表明变量之间存在严重的多重共线性。VIF的计算公式为:

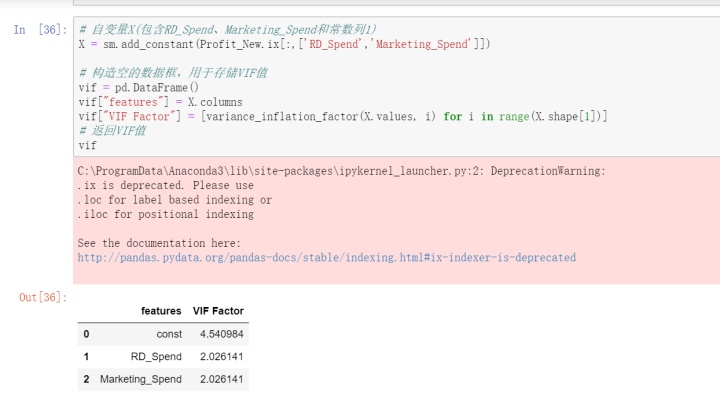
如上计算所示,两个自变量对应的方差膨胀因子均小于10,说明构建模型的数据并不存在多重共线性。
线性相关性检验
线性相关性即用于建模的因变量和自变量之间存在线性相关关系,可以使用Pearson相关系数和可视化方法进行识别,皮尔逊计算公式为:
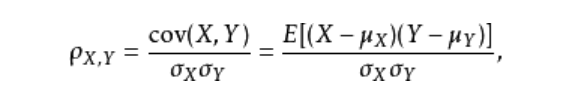

如上图结果所示,自变量中只有研发成本和市场营销成本与利润之间存在较高的相关系数,相关系数分别达到0.978和0.739,而其他变量与利润之间几乎没有线性相关性可言。以管理成本Administration为例,与利润之间的相关系数只有0.2,被认定为不相关,但是能说明两者不具有线性相关关系,当存在非线性相关关系时,皮尔逊系数也会很小,因此需要可视化的方法观测因变量和自变量之间的散点关系。可以使用seaborn模块中的pairplot函数。


从图中结果可知,研发成本和利润之间的散点图几乎为一条向上倾斜的直线(左下角),说明这两种变量之间确实存在很强的线性相关;市场营销成本与利润之间的散点图同样向上倾斜,但也有很多点的分布还是比较分散的(见第一列第三行);管理成本和利润之间的散点图呈水平趋势,而且分布也比较宽,说明两者之间确实没有任何关系(第一列第二行)。
以重构的model2为例,综合考虑相关系数,散点图矩阵和t检验的结果,最终确定只保留model2中的RDSpend和Marketing_Spend两个自变量,下面重新对该模型做修正。
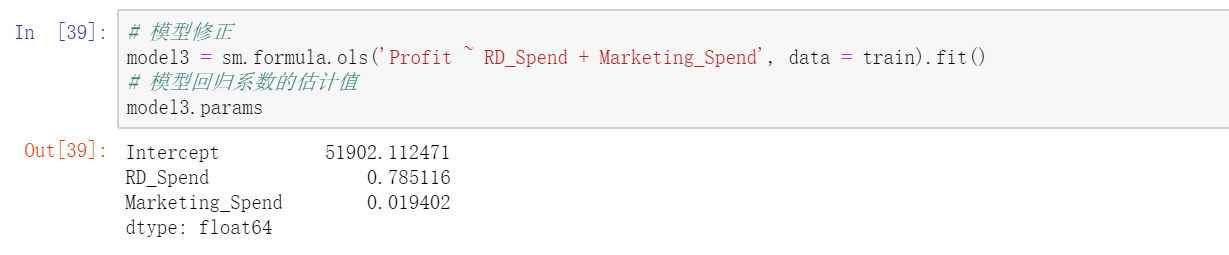
异常值检验
由于多元线性回归模型容易受到极端值的影响,故需要利用统计方法对观测样本进行异常点检测。如果在建模过程发现异常数据,需要对数据集进行整改,如删除异常值或衍生出是否为异常值的哑变量。对于线性回归模型,通常利用帽子矩阵,DFFITS准则,学生化残差或cook距离进行异常点检测。基于get_influence方法获得四种统计量的值。
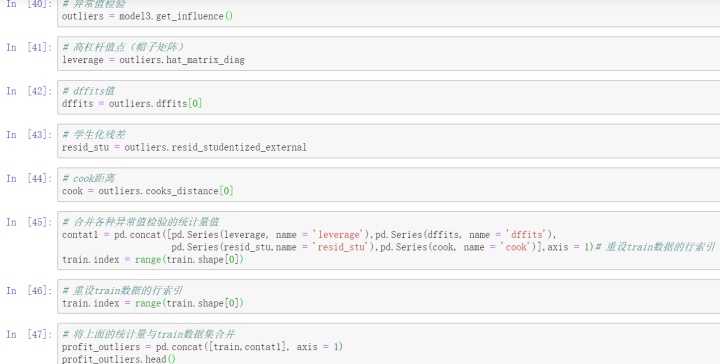
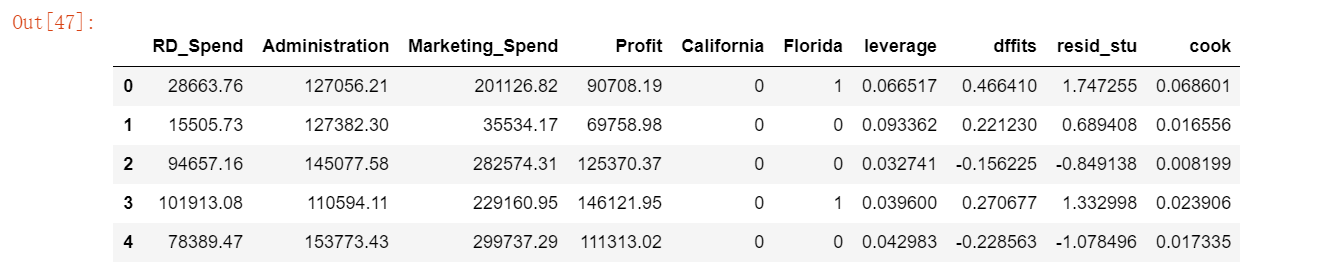
以上合并了四种统计量的值,这里使用标准化残差法将异常值查询出来,当标准化残差大于2时,即可认为对应的数据点为异常值。

异常比例为2.5%,比较小,故考虑将其删除。
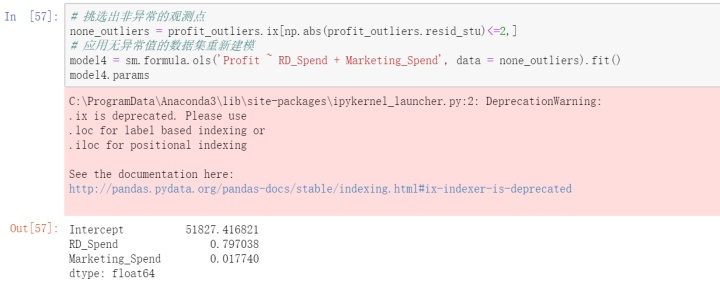
新的模型公式为:Profit=51827.42+0.80RD_Spend+0.02Marketing_Spend
独立性检验
残差e的独立性检验也就是因变量y的独立性检验。通常使用Durbin-Watson统计值来测试,如果DW值在2 左右,则表明残差之间时不相关的;如果与2偏离的教员,则说明不满足残差的独立性假设。
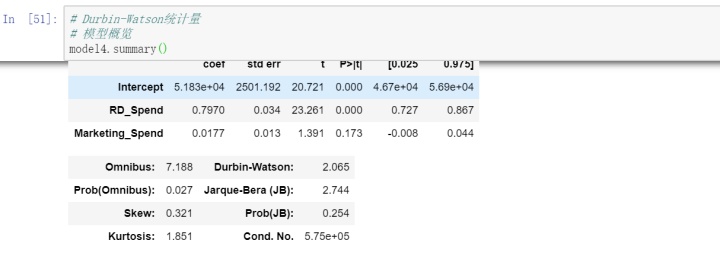
DW统计量的值为2.065,比较接近于2,故可以认为模型的残差项之间是满足独立性这个假设前提的。
方差齐性检验
方差齐性是要求模型残差项的方差不随自变量的变动而呈现某种趋势,否则,残差的趋势就可以被自变量刻画。关于方差齐性的检验,一般可以使用两种方法,即图形法(散点图)和统计检验法(BP检验)。
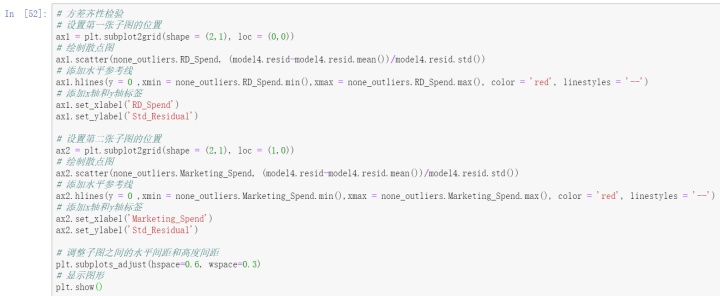
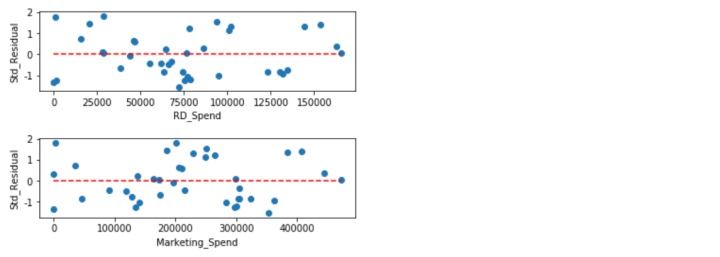
如图所示,标准化残差没有随自变量的变动而呈现喇叭性,所有的散点几乎均匀的分布在参考线y=0的附近。所以,可以说明模型的残差项满足方差齐性的前提假设。
经过前文的模型构造、假设检验和模型诊断,最新红确定合理的模型model4。接下来就是利用测试集完成预测。
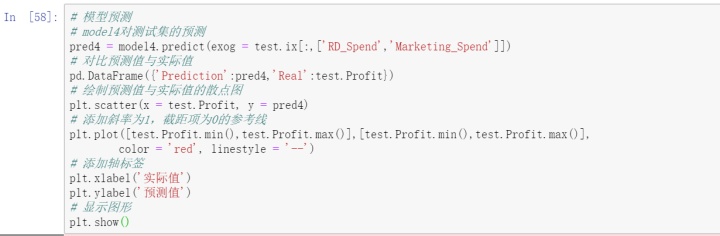
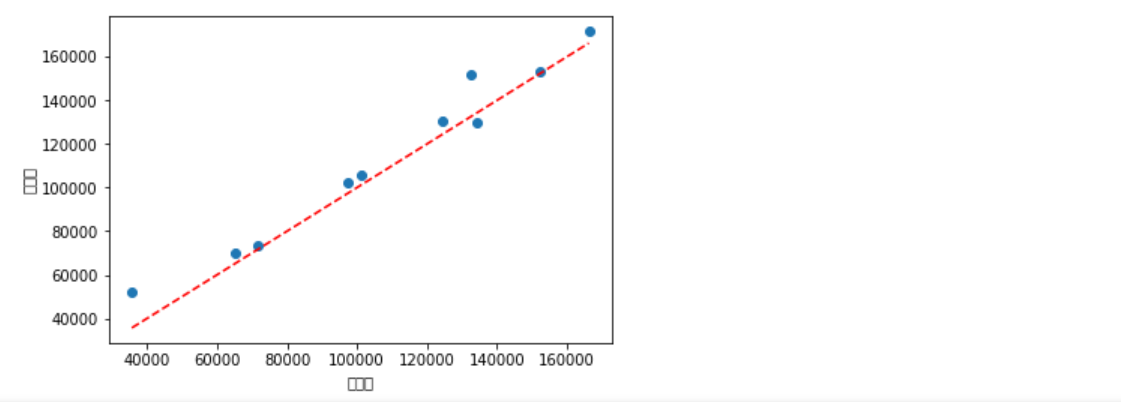
如上图所示,绘制了有关模型在测试集上的预测值和实际值的散点图。两者非常接近,散点在直线附近波动,说明模型的预测效果还是不错的。

)

)


)




)




)


