图:
图结构区别于线性结构和树型结构,区别可见下图
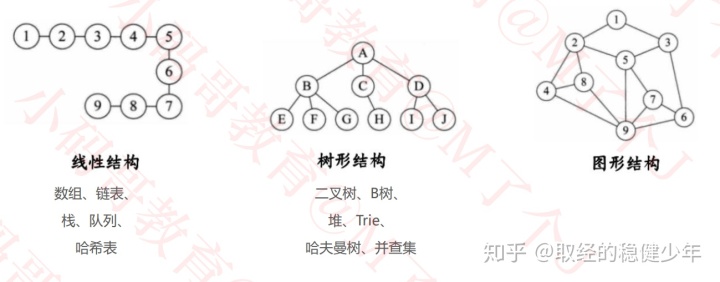
逻辑上的图(graph)结构由顶点(vertex)和边(edge)组成。
一个图结构G包含顶点集合V和边集合E,任何两个顶点之间可以有一个边表示两者的关系。
对于一个存在的G,V不可以为空集,E可以为空集。
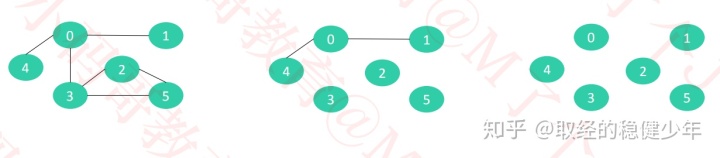
与图相关的概念:
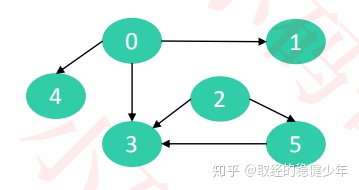
有向图:
边都具有方向的图结构就是有向图结构。边的方向表示访问的方向。
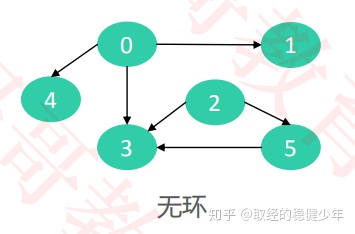
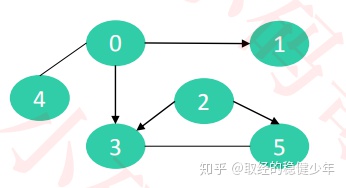
有向无环图:
对于一个有向图,如果对于任意一个节点来说,从该这一个结点起,不存在路径使得可以重新回到这一结点上,这个有向图就是有向无环图。
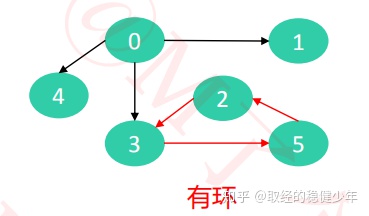
有向有环图:
与有向无环图相反。
入度,出度:
这一概念只适用于有向图。对于有向图种,一个指向一个顶点的边数量称为个顶点的入度,从这个顶点指出的边的数量称为这个顶点的出度。
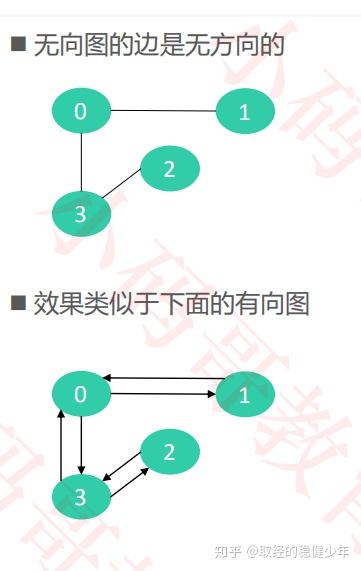
无向图:
无向图中,连接两个顶点的边是没有方向的,可以在逻辑上认为是两个顶点间如果有边直接连通,则一定两个方向都有的有向图。
混合图:
混合图种既存在有向边,也存在无向边。
简单图、多重图:
如果在无向图中,直接连通两个顶点的边大于等于2条,这些边称为平行边。
如果在有向图中,直接连通两个顶点的同方向的边大于等于2条,这些边称为平行边。
如果在图中一条边直接连通同一个顶点,就成为自环。
如果在图结构中存在平行边或者自环,这个图就称为多重图,如果两者都不存在,那么称为简单图。
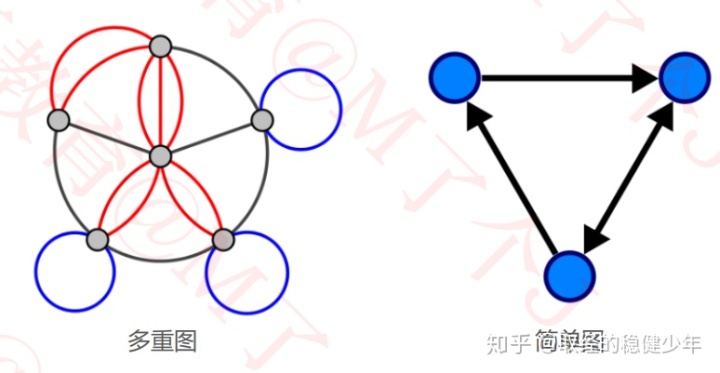
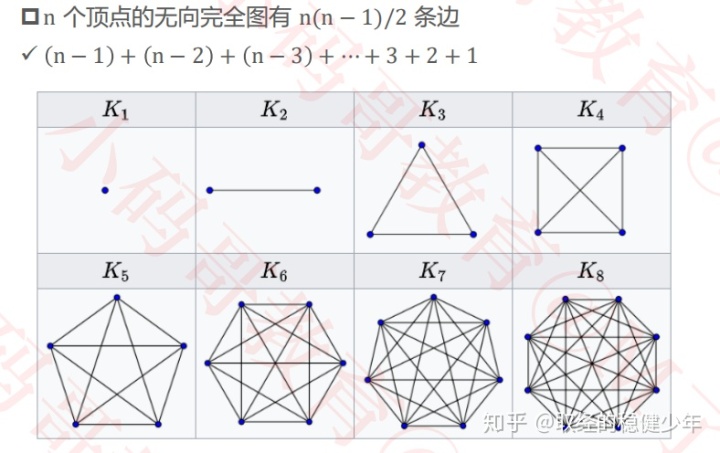
无向完全图、有向完全图:
如果在无向图中任意两个顶点之间都存在直接连通两个顶点的边,那么这个无向图就成为无向完全图。
如果在有向图中任意两个顶点之间都存在方向相反的直接连通两个顶点两个边,那么这个有向图就成为有向完全图。
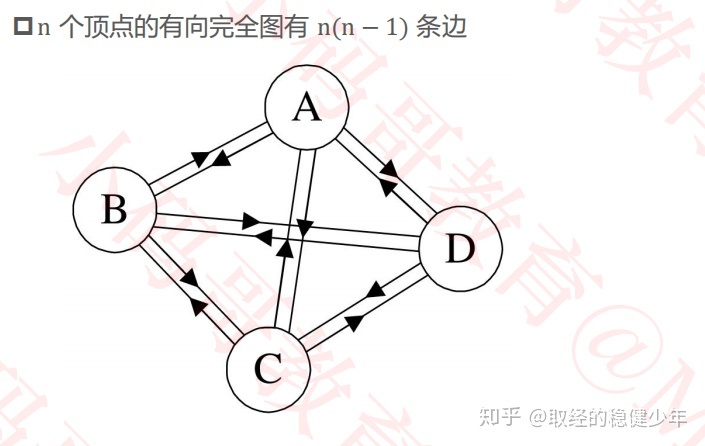
稠密图、稀疏图:
边数接近于完全图的图就是稠密图,边数远远少于完全图的图就是稀疏图。
有权图:
连接顶点的边上带有权值的图称为有权图
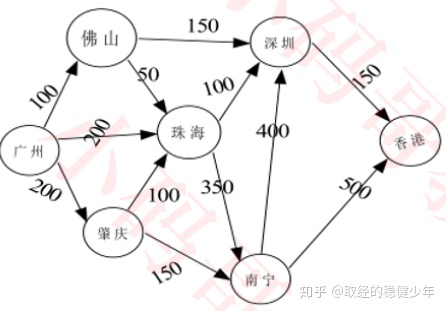
连通图:
如果无向图中任意两个顶点都可以连通,无论是间接还是直接,那么这个无向图称为连通图。
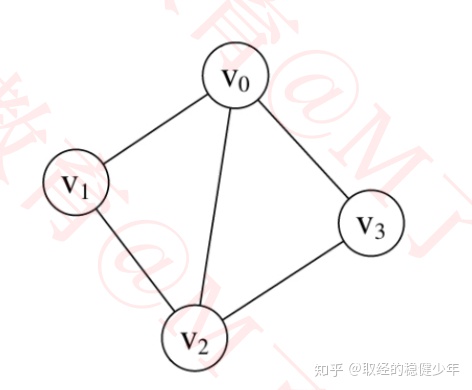
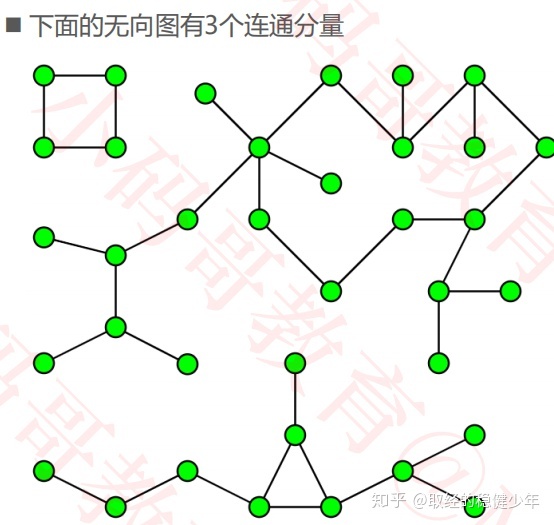
连通分量:
连通分量就是无向图中的最大连通子图数量,也就是一个无向图分出来的最多的互不连通的部分。对于一个连通图来说,连通分量为1。
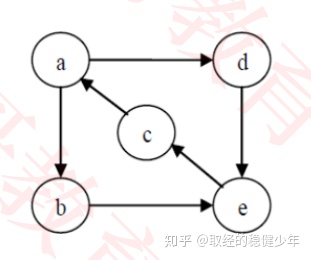
强连通图:
强连通图就是对有向图定义的连通图。
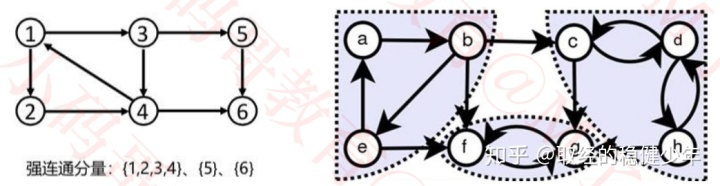
强连通分量:
同无向图的连通分量概念。
图的实现:
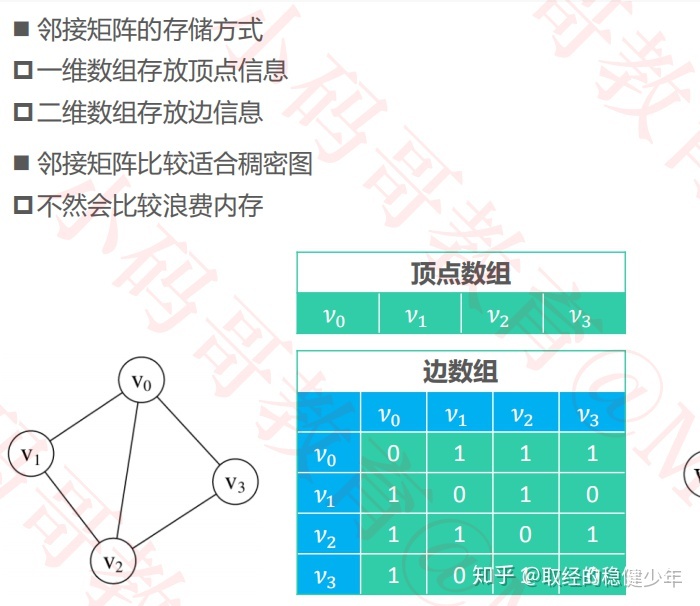
图一般有两种实现方法,一种是邻接矩阵,还有一种是邻接表,邻接矩阵实际操作比较复杂,这里主要写邻接表的代码实现。
图的邻接矩阵实现:
无向图
有向图
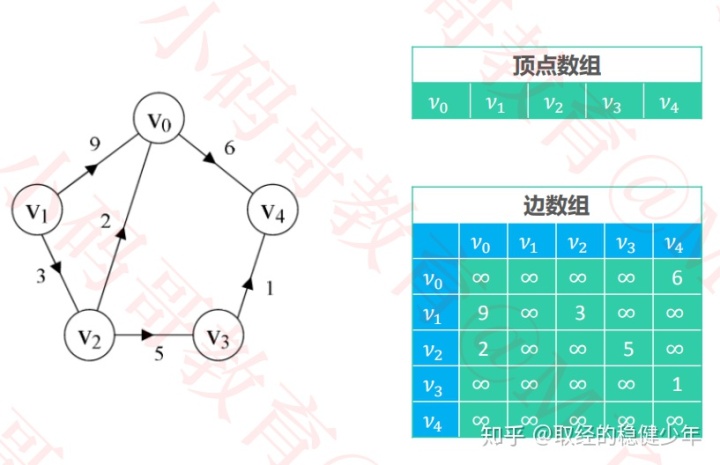
图的邻接表实现:
图的邻接表实现主要是分别将结点和边存放在结构体中,再以一定的方式将这些结构联系起来。以下实现代码主要使用哈希map来实现有向有权图,代码总体还是以表现思路为主。
//有向有权图的顶点结构,假定顶点存储的元素为int类型
图的遍历:
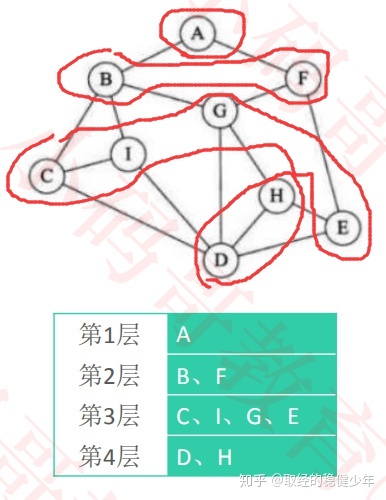
广度优先搜索(BFS):
广度优先搜索类似于二叉树的层序遍历。从一个指定的顶点开始,将指定的顶点视作逻辑上的第一层,指定的顶点所连通的顶点视作逻辑上的第二层,指定的顶点所联通的顶点所连通的顶点视作逻辑上的第三层,以此类推依次遍历,直到遍历完所有顶点。
//图结构的广度优先遍历
由以上的广度优先遍历实现代码可知,广度优先遍历上逻辑上下一层的元素一定是再当前层元素之后被访问,但是逻辑上同一层的元素的访问先后次序没有规律,这取决于outEdges这一set结构中的存储顺序。
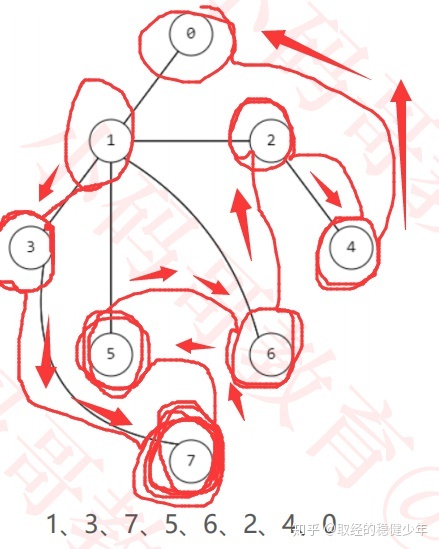
深度优先搜索(DFS):
深度优先搜索的思路类似于二叉树的先序遍历,从指定的顶点开始,访问该顶点后继续访问该顶点的逻辑上下一层的第一个顶点,以此类推直到不存在下一层的顶点,那就返回倒数第二层层的第二个顶点的位置继续重复以上操作,直到所有的顶点都被遍历。
//图的深度优先遍历
有向图的应用:AOV网(Activity On Vertex Network)
一项大的工程经常被分为多个小的子工程,多个子工程之间可能存在一定的先后顺序,也就是说某些子工程必须在其他子工程完成后才能开始。因此,在现代化管理中,人们常用有向图来描述和分析一项大工程的计划和实施过程,子工程被称为活动(Activity),在有向图中用顶点来表示,有向边表示活动之间的向后关系,这样的图结构称为AOV网。
结构:
标准的AOV网结构是一个有向无环图。
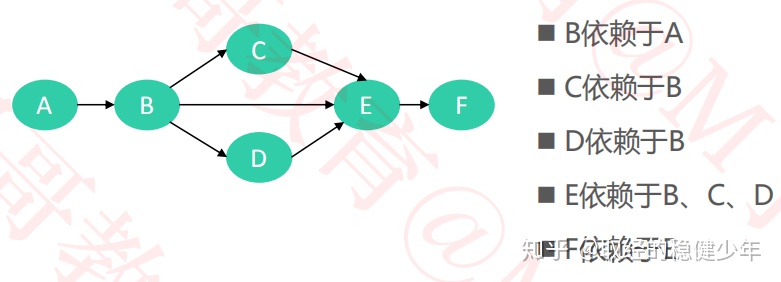
拓扑排序:
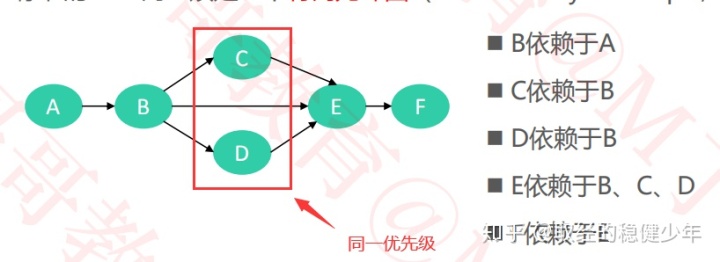
将AOV网中的所有顶点按活动的发生顺序排成一个序列,该序列一定满足活动发生的先后顺序,但同一优先级的活动的顺序不一定。比如说下图的排序结果是ABCDEF或者ABDCEF。
用卡恩算法实现AOV网的拓扑排序:
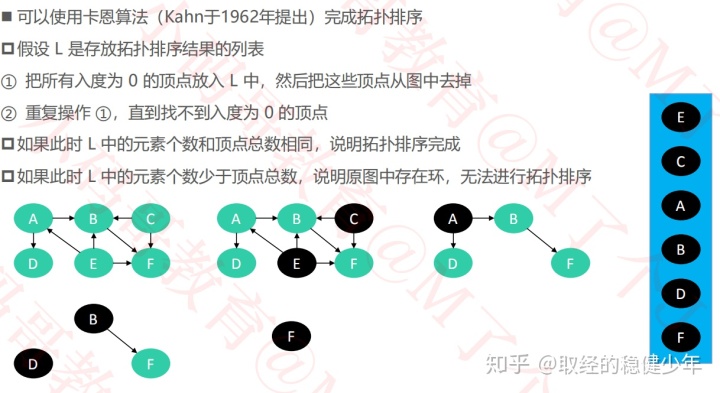
算法实现(仅仅体现思路)
//假定之前写的Graph就是AOV结构



)






)

)


:城市选择页(中))


)
