1. 题目

There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive).
The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi.
Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.

You want to determine if there is a valid path that exists from vertex start to vertex end.

Given edges and the integers n, start, and end, return true if there is a valid path from start to end, or false otherwise.

Example 1:

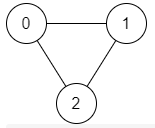
Input: n = 3, edges = [[0,1],[1,2],[2,0]], 
start = 0, end = 2
Output: true
Explanation: There are two paths from vertex 0 to vertex 2:
- 0 → 1 → 2
- 0 → 2

Example 2:

Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], 
start = 0, end = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.Constraints:
1 <= n <= 2 * 10^5
0 <= edges.length <= 2 * 10^5
edges[i].length == 2
1 <= ui, vi <= n - 1
ui != vi
1 <= start, end <= n - 1
There are no duplicate edges.
There are no self edges.

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-if-path-exists-in-graph
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

• 图的遍历，BFS、DFS都可以

class Solution:def validPath(self, n: int, edges: List[List[int]], start: int, end: int) -> bool:from queue import Queueg = [[] for _ in range(n)]for e in edges:g[e[0]].append(e[1])g[e[1]].append(e[0])vis = [0]*nq = Queue()q.put(start)vis[start] = 1while not q.empty():id = q.get()if id == end:return Truefor nid in g[id]:if vis[nid] == 0:vis[nid] = 1q.put(nid)return False

312 ms 66.1 MB Python3

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！