#时间预测算法_改进的智慧交通系统出行时间预测算法

引用

Chowdhury N K, Leung C K S. Improved travel time prediction algorithms for intelligent transportation systems[C]//International Conference on Knowledge-Based and Intelligent Information and Engineering Systems. Springer, Berlin, Heidelberg, 2011: 355-365.

摘要

出行时间预测为通勤者提供有用的信息，使他们能够决定是否对他们的路线或出发时间进行必要的更改。这解释了为什么旅行时间预测对于智能系统，尤其是智慧交通系统(ITS)变得重要。在过去的几年中，已经开发了几种算法来预测出行时间，但是其中一些存在一些问题。在本文中，我们提出了解决这些问题并提高 ITS 出行时间预测性能和/或准确性的算法。

介绍

由于出行时间预测对于许多智能交通系统(ITS)应用(例如动态路线导航和行程计划)至关重要，因此它在 ITS 中起着关键作用。随着高级出行者信息系统的发展，出行时间预测已变得越来越重要可以帮助通勤者更好地调整他们的出行时间表。此外，对于许多动态路线导航系统而言，准确可靠的道路行驶时间预测也至关重要，因为这种预测有助于通勤者确定他们是否需要更改路线的起始时间甚至取消行程。此外，准确的行进时间预测可以在起点和目的地之间生成最快的路径(参见最短的路径)。由于交通流量的时变特征(例如区分高峰时段交通与非高峰时段交通的每日特征)会影响准确出行时间的估计，因此如何提供可靠的出行时间信息已引起许多研究人员的关注。

在本文中，我们的主要贡献是提出了几种旅行时间预测算法，它们可以进一步提高现有算法的准确性和/或性能。具体来说，我们提出了快速准确的算法来改善 ITS 的出行时间预测。

我们改进的出行时间算法

在本节中，我们研究了 SMA，CA 和 MKC 算法，并发现了它们相关的问题。然后，我们提出了解决这些问题并进一步提高行程时间预测的准确性和/或性能的几种算法。

改进的连续移动平均(iSMA)和改进的链平均(iCA)算法

SMA 和 CA 都存在以下问题：

问题 1. SMA 或 CA 所需的空间量与历史出行次数成指数关系。给定 n 个历史出行时间，SMA 和 CA 需要构造一个 n×n 矩阵(或更准确地说，是一个 n×n 上三角矩阵，其中 n(n + 1)/2 个非空条目)。

改进的 k 均值聚类(iMKC)算法

问题 4.差异度量未应用于规范化的三维空间。取而代之的是，它对三个维度中每个维度的两个历史数据 ti 和 tj 之和求和。不幸的是，每个维度使用了不同的单位(例如，以分钟为单位测量出行时间的差异，以 km / h 为单位测量速度的差异)。

问题 5.在相异性度量中使用的三个维度(即旅行时间和速度)中的两个是相关的。对于给定的路段(即具有固定距离)，行驶时间与其速度成反比，因为行驶时间 × 速度=道路段的距离。因此，保持两个维度变得多余。

解决方案：为了解决问题 4 和 5，我们提出了第三种算法。观察与 MKC 中使用的不相似度度量相关的问题，我们提出的改进的改进 k 均值聚类(iMKC)算法使用了一个不同但更合适的不相似度度量。具体来说，我们的 iMKC 仅基于两个唯一行驶时间 ti 和 tj 之间的差来测量差异：

通过这样做，我们的 iMKC 可以解决问题 4 和 5，因为它避免了测量两个相关的维度，并且不对以不同单位度量的差异求和。而且，它将聚类空间的维数从三个减少到一个。实验结果表明，我们的 iMKC 导致比 MKC 更为准确的预测。

增强方法一：尽管我们的 iMKC 解决了问题 4 和 5，但可以进一步增强它。例如，细心的读者可能会注意到，相异性度量仅度量了行进时间的成对差异。但是，在给定路段 S 和时间段 T 的情况下，在 n 个历史行驶时间的集合中重复行驶时间并不罕见。我们更好地记录了这些出行时间的频率。因此，我们对 iMKC 的第一个增强就是捕获此频率信息。代替增加维度并陷入以不同单位计量的数量之和的潜在问题，我们通过相应的频率 fi 和 fj 加权传播时间 ti＆tj：

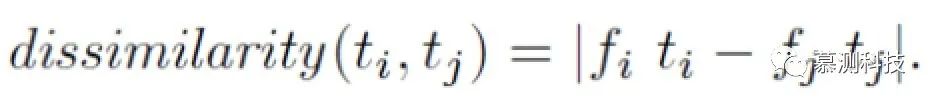
增强方法二：第一个增强功能侧重于差异度度量，而第二个增强功能侧重于聚类技术。由于 k-medoid 聚类通常比 k-means 聚类对噪声和离群值更鲁棒，因此我们对 iMKC 的第二个增强是使用 k-medoid 聚类。k 均值聚类和 k 质形聚类之间的主要区别在于，前者的聚类以质心表示(即，一个聚类中所有数据的中心)，而后者的聚类以质体表示(即位于最中心的数据每个群集)。由于 iMKC 使用迭代优化进行聚类，因此需要kn个比较才能在每次迭代中将 n 个旅行时间分配给 k 个聚类。尽管可能需要进行 n 个额外的比较才能找到 k 个质心，但很常见的是 k 个质心保持不变，而 k 个质心从一次迭代更改为另一个。因此，作为奖励，使用 k-medoid 可以减少迭代次数。实验结果表明，使用 k-medoid 聚类的这种增强的 iMKC 比使用 k-means 聚类的 iMKC 提供了更准确的预测出行时间(并且更有效)。

总结

在本文中，我们分析了三种现有算法(即 CA，SMA，MKC)，并揭示了它们的问题，并提出了五种算法(即 iCA，iSMA，iMKC 及其两个增强功能)作为解决这些问题并为 ITS 提升出行时间预测。我们提出的 iCA 和 iSMA 算法使用非递归方程式直接计算预测的出行时间。它们通过减少时间和空间要求，同时维持预测的准确性，改善了出行时间的预测过程。我们的 iMKC 算法降低了聚类空间的维数，并在一个旅行时间维中测量了不相似性。它提高了预测的准确性和性能。两项增强功能通过捕获差异度量中的行进时间频率和/或使用 k-medoid 聚类进一步改善了 iMKC。实验结果表明，我们提出的所有五种算法均改善了 ITS 的行程时间预测。