非线性回归（Non-linear Regression）

1.概率:
1.1定义概率Probability:对一件事情发生的可能性的衡量
1.2范围 0<=P<=1
1.3计算方法:
1.3.1根据个人置信
1.3.2根据历史数据
1.3.3根据模拟数据
1.4条件概率:（A发生的条件下B发生的概率）

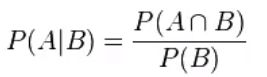
逻辑回归（Logistic Regression）
x∈（-∞，+∞），y∈（0,1）
2.1举例，肿瘤良恶性：

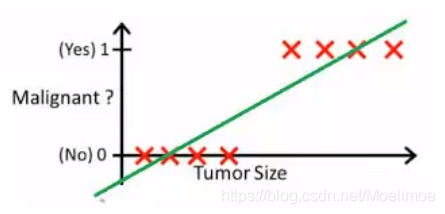
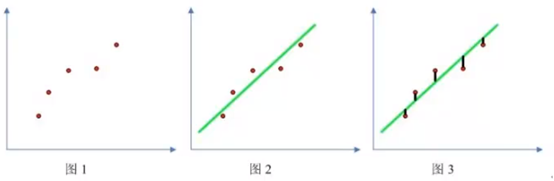
画出线性回归线，计算h(x)值若大于0.5，则认为是Malignant（恶性）.
特殊例子，出现一个偏离较大的数值：

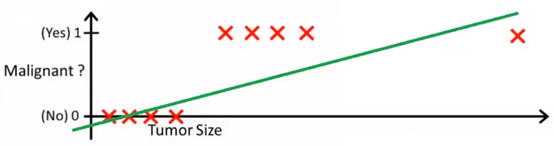
h(x)>0.5（恶性），Malignant=1
再重新模拟后的线性方程就无法准确分类了

2.2基本模型
测试数据为
$$X(x_0,x_1,x_2...x_n)$$
要学习的参数为:
$$\theta ({\theta }_0,{\theta }_1,{\theta }_2，...{\theta }_n)（\theta 可以是一个向量）$$

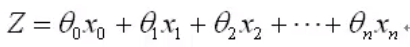
向量表示:（θ^T 为一列排列的θ）

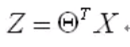
处理二值数据，引入Sigmoid函数时曲线平滑化：


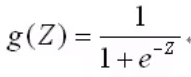
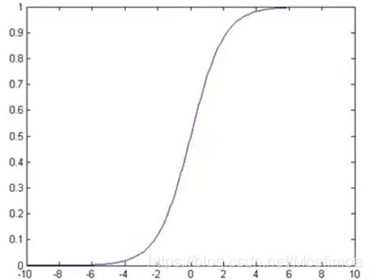
预测函数：

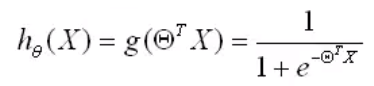
θ为参数，X为自变量

用概率表示
正例(y=1)：（对于给定的一组数据自变量和一组参数，y=1的概率）

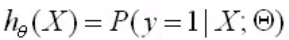
反例（y=0）：（对于给定的一组数据自变量和一组参数，y=0的概率）

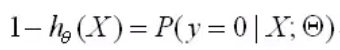
2.3 Cost函数
线性回归:


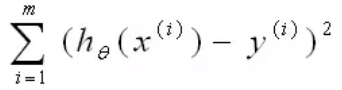
$$y^{(i)}$$为实例的值）$$x^{(i)}$$为每一个实例的自变量，求出的$$h_{\theta }(x^{(i)})$$即为预测值y_hat

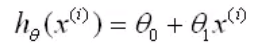
找到合适的θ_0，θ_1使_上式最小，求导数使其为0，即可求得

Logistic regression:
Cost函数:
（使用对数log的原因：对数是个增函数，很容易求出最大值和最小值，对原函数最大/最小化和对原函数它的对数最大化和最小化是一样的？可以使运算简单很多）

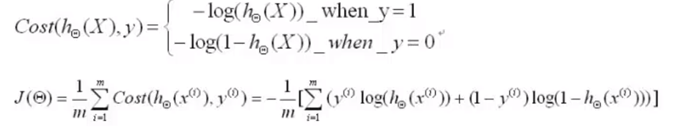
下方程由上面两个方程合成得到（分y=1和y=0）
目标: 找到合适的θ_0，θ_1使_上式J(θ)最小，求导数使其为0，即可求得
方法：数学上一般对其变量求偏导，是其偏导等于0

2.4解法:梯度下降(gradient decent)
一个计算机中非常重要的算法
梯度下降法是用负梯度方向为搜索方向的，最速下降法越接近目标值，步长越小，前进越慢。可以用于求解非线性方程组。
梯度下降法的计算过程就是沿梯度下降的方向求解极小值。


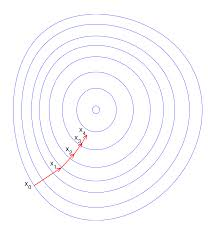
求偏导（求出斜率）找到曲面的最低点
（以θ对J求导数，α为学习率可能会随时变更，）
更新法则（化简上式后）：（i上标表示不同的实例）

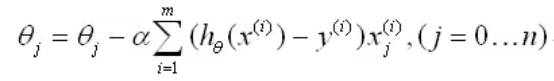
同时对所有的θ进行更新
重复更新直到收敛（低于设置的预测值，一般为local minimum or global minimum）

非线性回归实例应用（Logistic Regression Application）：

import numpy as np
import randomdef gradient_descent(x, y, theta, alpha, m, iteration_times):"""m denotes the number of examples here, not the number of featuresParameters----------------x: 实例y: 分类标签theta: 要学习的参数θalpha: learning ratem: 更新法则公式中实例的个数，对应示例数组shape[0]iteration_times: 使用此方法循环训练更新的次数"""for i in range(0, iteration_times):hypothesis = np.dot(x, theta)  # h(x) = x·θ，θ的shape已转换为能和x点乘，x无需转置，每次更新完后θ会发生变化loss = hypothesis - y  # hypothesis其实就是y_hat（估计值h(x)）,这里loss就等于y_hat减去y(实际)# avg cost per example (the 2 in 2*m doesn't really matter here.# But to be consistent with the gradient, I include it)'''cost：对精确度的衡量，会随着gradient descent的次数减小'''cost = np.sum(loss ** 2) / (2 * m)  # 这里的cost函数与课文中提到的cost函数不一样，这里使用了一个简单的cost便于计算和展示print('Iteration:%d|cost:%f' % (i, cost))# avg gradient per examplegradient = np.dot(loss.T, x) / m  # loss·x = (h(x)-y)·x，使用矩阵形式同时对所有x执行运算，loss要转置一下，theta要求平均值# updatetheta = theta - alpha * gradient  # 即更新法则的公式：θ=θ-α∑(h(x)-y)xreturn theta# 产生测试拟合的数据
def gen_data(num_points, bias, variance):"""Parameters---------num_points:实例数bias:生成y时产生一个偏差值variance:方差"""x = np.zeros(shape=(num_points, 2))y = np.zeros(shape=num_points)# basically a straight linefor i in range(0, num_points):# bias featurex[i][0] = 1x[i][1] = i# target variabley[i] = (i + bias) + random.uniform(0, 1) * variance  # random.uniform(0,1)[0, 1)均匀分布，同random.random()产生0~1随机数return x, ydef main():# generate 100 points with a bias of 25 and 10 variance as a bit of noisex, y = gen_data(100, 25, 10)print(x)print(y)m, n = np.shape(x)  # x是二维数组，行数赋值给m，列数赋值为na = np.shape(y)  # y是1维的数组，只会一个数值print(m, n)  # (100行，2列) 2维数组，100行2列print(a)  # (100，) 1维数组，100个数值iteration_times = 100000alpha = 0.0005  # 取0~1，比较好的算法会设置开始的alpha数值较大后期数值较小theta = np.ones(n)  # 初始化θ：[1. 1.] ，初始时x的值认为是h(x)的值theta = gradient_descent(x, y, theta, alpha, m, iteration_times)print(theta)  # 约为[30 1]# 得出的theta就可以用于对新实例的计算和预测# 回归算法和神经网络中都会用到此梯度下降的方法if __name__ == '__main__':main()