回归中的相关度和R平方值

自变量x和因变量y的相关度
1.皮尔逊相关系数(Pearson Correlation Coefficient):
1.1衡量两个值线性相关强度的量
1.2取值范围[-1,1]:
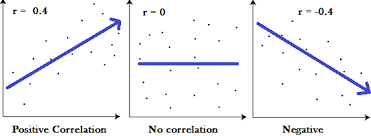
正向相关: >0,负向相关: <0,无相关性: =0
公式：correlation， correlationvariance(Cov)：协方差（两个量相关方差） Var：方差

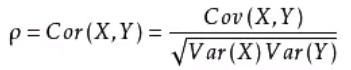
变化得：

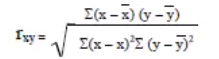
分子即为covariance，分母中开根号抵消一个Cov得到当前的分母.
2. 计算方法举例：
| X | Y |
| 1 | 10 |
| 3 | 12 |
| 8 | 24 |
| 7 | 21 |
| 9 | 34 |
正相关；无相关；负相关：

4. R平方值:（衡量做出的模型能多大比例解释y的变化）
4.1定义:决定系数，反应因变量的全部变异能通过回归关系被自变量解释的比例。
4.2描述:如R平方为0.8,则表示回归关系可以解释因变量80%的变异。换句话说，如果我们能控制自变量不变，则因变量的变异程度会减少80%
4.3 :简单线性回归: R^2= r* r（一个自变量x和一个因变量y）
多元线性回归:

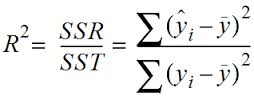
SSR:Sum Square of Regression（由于建的模型不完全与数据一致而引起的变异程度的平方和）
SST:Sum Square of Total（所有点的变异量的平方和）
y_hat：为估计值，在模型线上；
y_bar：为平均值，所有y求均值；
y(i):即为实际的y的值
SSE：Sum Square of Error（自然误差浮动）（SSE+SSR=SST）

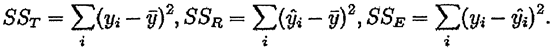
那么R^2=SSR/SST即表示我们的模型能表示该变异程度的所占比例
（绿线为对应的y为y的均值）

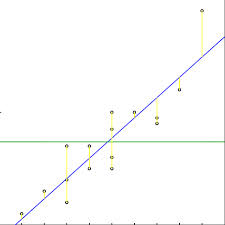
一般0.3~0.8表示拟合度较高

5. R平方也有其局限性: R平方随着自变量（样本）的增加会变大，R平方和样本量是有关系的。因此，我们要到R平方进行修正。修正的方法:
   
   变量说明见图片中描述
   R^2_adjusted用来评判线性模型对数据的拟合度的好坏

实例代码：

import numpy as np
import mathdef computeCorelation(X,Y): #计算corelationX_Bar = np.mean(X)Y_Bar = np.mean(Y)CovXY = 0var_X = 0var_Y = 0for i in range(0,len(X)):#对于所有的数据# 求corelation(X,Y)或者说求r_XYdiff_XXBar = X[i]-X_Bardiff_YYBar = Y[i]-Y_BarCovXY += (diff_XXBar*diff_YYBar)var_X += diff_XXBar**2var_Y += diff_YYBar**2VarXY = math.sqrt(var_X*var_Y)return CovXY/VarXY
#对于简单线性回归只需将此值平方即可得到R平方值testX = [1,3,8,7,9]
testY = [10,12,24,21,34]
print('r:',computeCorelation(testX,testY))
print('r*r:',computeCorelation(testX,testY)**2)# polynomial Regression
def polyfit(x,y,deg=1): #degree为方程的最高次方,这里为2元1次回归方程,deg=1results= {}coeffs = np.polyfit(x,y,deg=1)#polyfit可以在传入参数后自动计算出回归方程得到方程的各个斜率截距等参数results['polynomial'] = coeffs.tolist() #numpy中的list转换方法，只能用于数组、矩阵p = np.poly1d(coeffs) y_hat = p(x) #调用np中的1维的方程计算方法可以直接计算预测值y_haty_bar = np.mean(y)SSR = np.sum((y_hat-y_bar)**2) SST = np.sum((y-y_bar)**2)results['determination'] = SSR/SSTprint('results:',results) #polynomial的两个值对应斜率和截距return resultsprint('r^2：',polyfit(testX,testY)['determination'])

运行结果如下：

r: 0.94031007654487
r*r: 0.8841830400518192
results: {‘polynomial’: [2.65677966101695, 5.322033898305076], ‘determination’: 0.8841830400518196}
r^2： 0.8841830400518196