同学你好!本文章于2021年末编写,已与实际存在较大的偏差!
故在2022年末对本系列进行填充与更新,欢迎大家订阅最新的专栏,获取基于Pytorch1.10版本的理论代码(2023版)实现,
Pytorch深度学习·理论篇(2023版)目录地址为:
CSDN独家 | 全网首发 | Pytorch深度学习·理论篇(2023版)目录本专栏将通过系统的深度学习实例,从可解释性的角度对深度学习的原理进行讲解与分析,通过将深度学习知识与Pytorch的高效结合,帮助各位新入门的读者理解深度学习各个模板之间的关系,这些均是在Pytorch上实现的,可以有效的结合当前各位研究生的研究方向,设计人工智能的各个领域,是经过一年时间打磨的精品专栏!https://v9999.blog.csdn.net/article/details/127587345欢迎大家订阅(2023版)理论篇
以下为2021版原文~~~~

1.数组样例


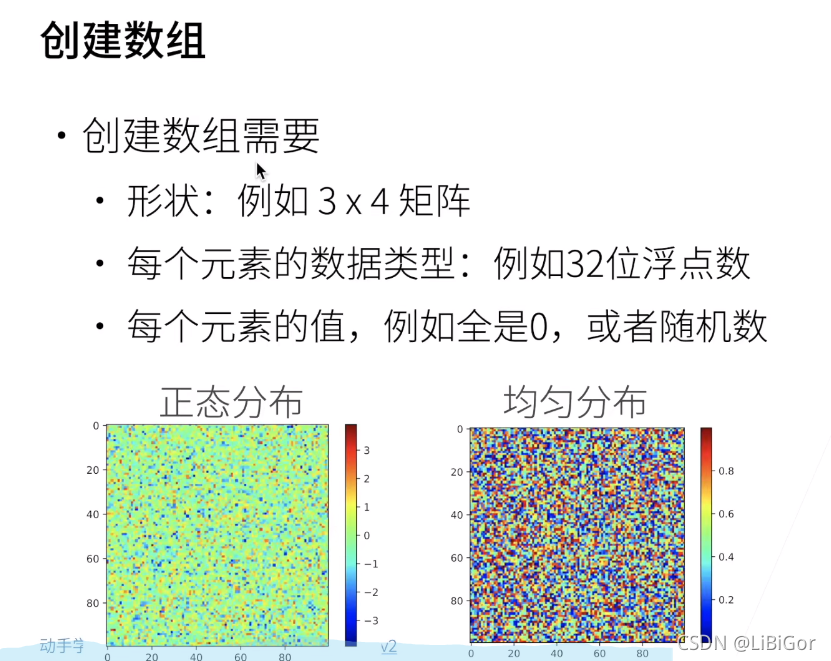
2.数据操作(代码实现与结果截图)
#首先导入torch,虽然被称为pytorch,但是我们应该导入torch而不是pytorch
import torch#张量表示一个数值组成的数组,这个数字可能有多个维度
#这个行向量包含从0开始的前12个整数,默认创建为浮点数。张量中的每个值都称为张量的元素(element)。
#例如,张量x中有12个元素。除非额外指定,否则新的张量将存储在内存中,并采用基于CPU的计算。
x=torch.arange(12)x
x.shape() #shape不是函数哦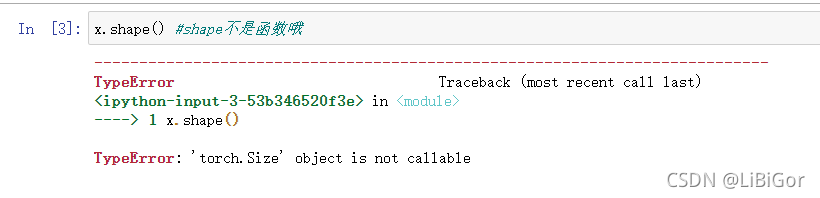
#通过张量的shape属性来访问张量的形状 (沿每个轴的长度)
x.shape
x.numel() #x的总数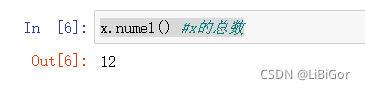
#要改变一个张量的形状,而不改变元素的数量和元素值,我们可以调用reshape()
#注意,通过改变张量的形状,张量的大小不会改变。
x = x.reshape(3,4)
x#不需要通过手动指定每个维度来改变形状。
#如果我们的目标形状是(高度,宽度),那么在知道宽度后,高度应当会隐式得出,我们不必自己做除法。在上面的例子中,为了获得一个3行的矩阵,我们手动指定了它有3行和4列。幸运的是,张量在给出其他部分后可以自动计算出一个维度。
#可以通过在希望张量自动推断的维度放置-1来调用此功能。
#即 x.reshape(-1,4) 或 x.reshape(3,-1) 等价于 x.reshape(3,4)。
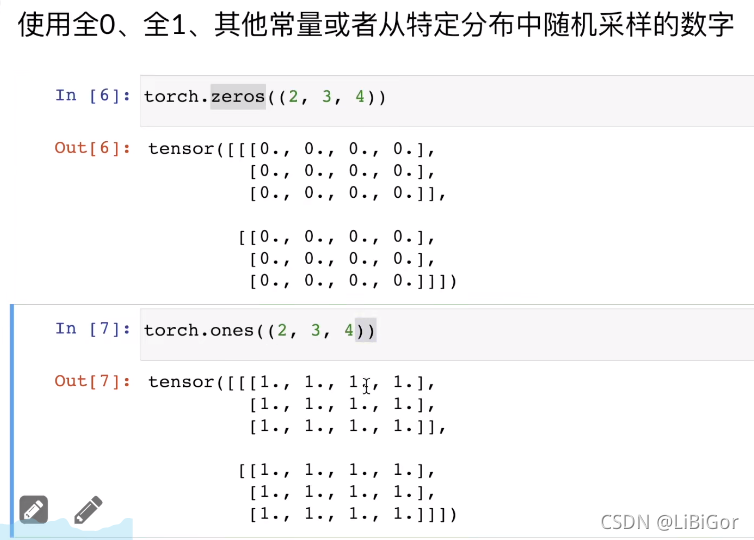
#使用全0的张量
torch.zeros((2,3,4))
#使用全1的张量
torch.ones((2,3,4))
#使用包含数值的python列表给张量中的每个元素赋予确定值
torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]])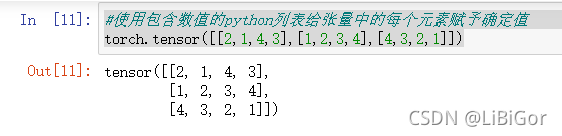
#标准算数运算符可以升级为按照元素运算
x = torch.tensor([1.0,2,4,8])
y = torch.tensor([2,2,2,2])
x + y,x - y,x * y,x / y, x**y # **运算符是求幂运算
#创建一个形状为(3,4)的张量。其中的每个元素都从均值为0、标准差为1的标准高斯(正态)分布中随机采样。
torch.randn(3, 4)tensor([[-0.9464, 0.7712, -0.0070, 1.0236],[-2.1246, -0.7854, -1.9674, -0.1727],[ 0.0397, -0.0477, -0.0160, -0.0113]])
#按元素的方式进行更多的计算
torch.exp(x)
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
torch.cat((X,Y),dim=0), torch.cat((X,Y),dim=1) #dim=0按列排列 #dim=1按行排列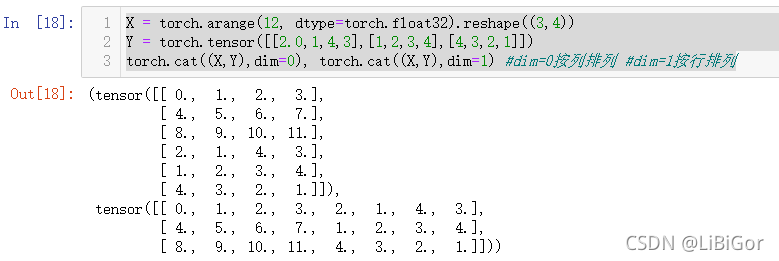
#通过逻辑运算符构建二元张量
X == Y
#对于每个位置,如果X和Y在该位置相等,则新张量中相应项的值为1,这意味着逻辑语句X == Y在该位置处为真,否则该位置为0。
#对于张量中的所有元素求和会产生只有一个元素的张量
X.sum()
2.1.3广播机制
在某些情况下,即使形状不同,我们仍然可以通过调用广播机制(broadcasting mechanism)来执行按元素操作。这种机制的工作方式如下:首先,通过适当复制元素来扩展一个或两个数组,以便在转换之后,两个张量具有相同的形状。其次,对生成的数组执行按元素操作。
#形状不同 张量会进行广播机制
a = torch.arange(3).reshape((3,1))
b = torch.arange(2).reshape((1,2))
a,b #广播机制
#由于a和b分别是 3×1 和 1×2 矩阵,如果我们让它们相加,它们的形状不匹配。我们将两个矩阵广播为一个更大的 3×2 矩阵,如下所示:矩阵a将复制列,矩阵b将复制行,然后再按元素相加。
a + b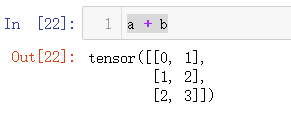
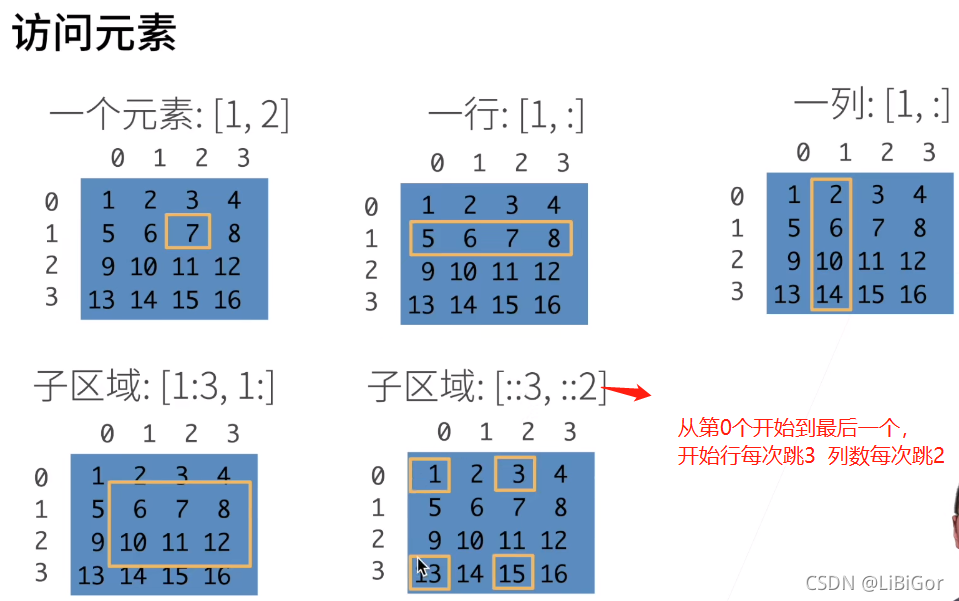
#[-1]选择最后一个元素,[1:3]选择第二个和第三个元素
X[-1],X[1:9] #1到9 但是最多有2行所以就显示了第1行和第2行
#通过指定索引来将元素写入矩阵
X[1,2]=9
X
#为多个元素赋相同的值
X[0:2,:] =12 #将0至2行,全部赋值为12
X
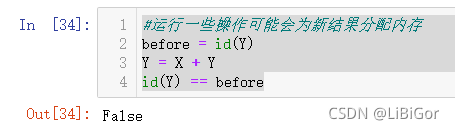
#运行一些操作可能会为新结果分配内存
before = id(Y)
Y = X + Y
id(Y) == before#执行原地操作 内存没有变化
Z = torch.zeros_like(Y)
print('id(Z)',id(Z))
Z[:] = X + Y
print('id(Z)',id(Z))
#如果后续计算中没有重复使用x,我们可以使用x[:]=X+Y 或者 x+=y来减少操作的内存开销
before = id(X)
X += Y #+=的本质是调用append()
id(X) == before
A = X.numpy() #转化为numpy张量
B = torch.tensor(A)
type(A),type(B)
a = torch.tensor([3.5])#将大小为1的张量转化为python的标量
a,a.item(),float(a),int(a)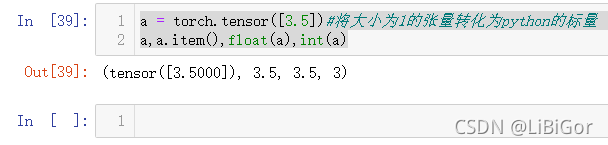
3.csv的读取(代码实现与结果截图)
我们将简要介绍使用pandas预处理原始数据并将原始数据转换为张量格式的步骤。我们将在后面的章节中介绍更多的数据预处理技术。
import os
#创建一个人工数据集并且存储在csv(逗号分割值)的文件中
os.makedirs(os.path.join('..','data'),exist_ok=True)
data_file = os.path.join('..','data','house_tiny.csv')
with open(data_file,'w') as f:f.write('NumRooms,Alley,Price\n') # 列名f.write('NA,Pave,127500\n') # 第1行的值f.write('2,NA,106000\n') # 第2行的值f.write('4,NA,178100\n') # 第3行的值f.write('NA,NA,140000\n') # 第4行的值
import pandas as pd
#从创建的csv文件中加载原始数据集
data = pd.read_csv(data_file)
print(data)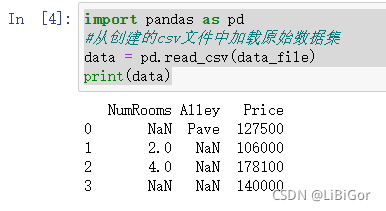
data
#注意,“NaN”项代表缺失值。为了处理缺失的数据,典型的方法包括插值和删除,其中插值用替代值代替缺失值。而删除则忽略缺失值。在这里,我们将考虑插值。#通过位置索引iloc,我们将data分成inputs和outputs,其中前者为data的前两列,而后者为data的最后一列。对于inputs中缺少的数值,我们用同一列的均值替换“NaN”项。
inputs,outputs = data.iloc[:,0:2],data.iloc[:,2]
inputs = inputs.fillna(inputs.mean()) #在缺失数据处 添加平均值
print(inputs) 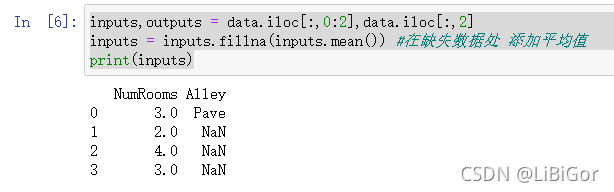
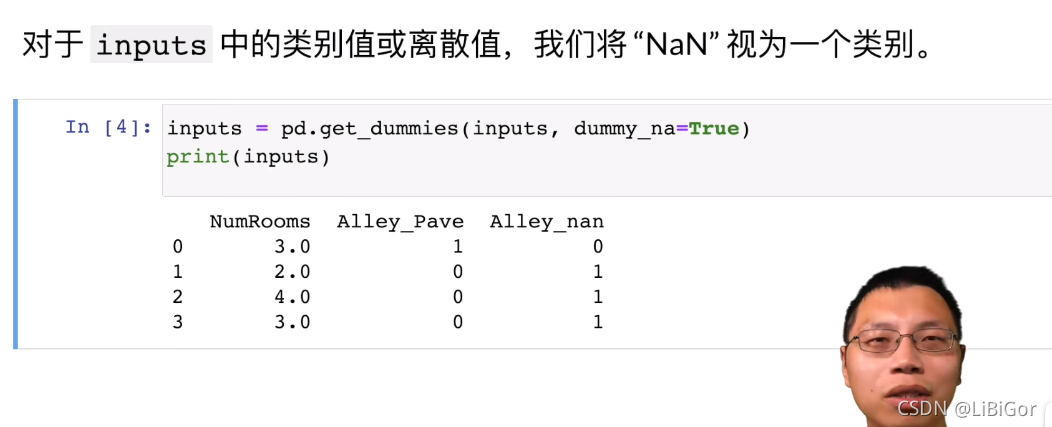
#对于inputs中的类别值或离散值,我们将NaN视为一个类别
inputs = pd.get_dummies(inputs,dummy_na=True) #按类分
print(inputs) 
import torch
X, y = torch.tensor(inputs.values),torch.tensor(outputs.values)
X, y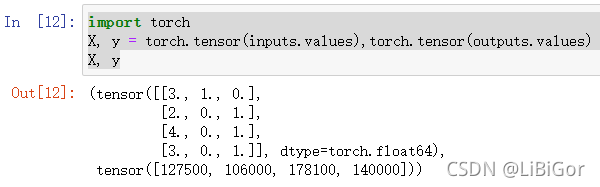
3.QA
1. b=a.reshape 并没有申请新的内存空间

2.学习一下numpy
3.快速区分维度:a.shape
4.视频笔记截图






















 -- Spark安装及简介)







 Practise 1045 快速排序(离散化+主席树区间内的区间求和))







中检测车道线+代码实现)

)