图的搜索
深度优先搜索(Depth First Search)
定义
从例子出发理解
- DFS是一种用于遍历或搜寻树类或图类数据结构的算法,这种算法从根结点出发(如果是图,则任意选择一个顶点作为根结点),在回溯之前会尽可能地遍历每一个分支。
- DFS类似于树的先序遍历
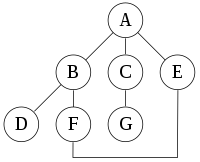
假设根结点为A,左结点优先于右结点,并且不会重复遍历,
则上图的DFS路径:A→B→D→F→E→C→G
如果不遍历时不标记已遍历过的结点,则会重复遍历,
DFS路径会是:A→B→D→F→E→A,循环无法结束
从即将实现的代码设计中理解
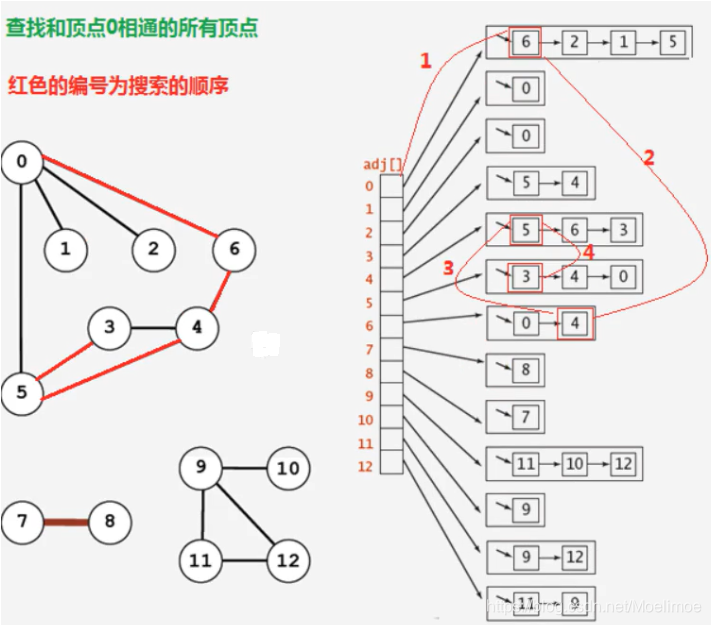
- 指定一个索引如0对其进行DFS,
- 在其存放相连结点的队列queue中按顺序获取子结点,第一个为6,标记6为已搜寻
- 然后对6的子结点,按顺序搜索,第一个为0,0在最开始就提前标记已搜寻,
- 转向第二个子结点4,标记4为已搜寻,
- 接下来对4的子结点搜寻,以此类推直到搜寻到一个结点它的所有子结点都被搜寻过了
- 就往回后退,后退过程中逐个检查是否存在未搜寻的结点,如果有则搜寻,否则回到最初的0结点,进行下一个子结点搜寻
方法与属性设计
- self.G 接收传入的无向图(上一节实现的)
- self.marked 标记已经遍历过的顶点,True为标记,False为未标记
- self.count 对顶点计数,初始值为0,运行完代码它应该为顶点的数量
- is_marked() 返回marked的值
- dfs()对图进行深度优先搜索
- count_all_connected()返回所有相连的顶点(count)
Python代码实现
from Structure.graph.Undigraph import Undigraphclass DepthFirstSearch:def __init__(self, graph, x):"""The vertex [x] is also a index of the graph G"""self.G = graphself.marked = [False for _ in range(self.G.vertex)]self.count = 0 # Count the vertices connected with the vertex xself.dfs(x)def is_marked(self, x):return self.marked[x] is Truedef dfs(self, x):self.marked[x] = Trueedges = self.G.get_edges_of(x)for n in edges:if not self.marked[n]:self.dfs(n)self.count += 1def count_all_connected(self):return self.countif __name__ == '__main__':UG = Undigraph(13)UG.add_edge(0, 5)UG.add_edge(0, 1)UG.add_edge(0, 2)UG.add_edge(0, 6)UG.add_edge(5, 3)UG.add_edge(5, 4)UG.add_edge(3, 4)UG.add_edge(4, 6)UG.add_edge(7, 8)UG.add_edge(9, 10)UG.add_edge(9, 11)UG.add_edge(9, 12)UG.add_edge(11, 12)vertex1 = 0DFS = DepthFirstSearch(UG, vertex1)print(f"Count all the vertices connected with the vertex[{vertex1}]: {DFS.count_all_connected()}")vertex2 = 5print(f"If vertex[{vertex2}] is connected with vertex[{vertex1}]? {DFS.is_marked(vertex2)}")vertex3 = 7print(f"If vertex[{vertex3}] is connected with vertex[{vertex1}]? {DFS.is_marked(vertex3)}")
运行结果
Count all the vertices connected with the vertex[0]: 7
If vertex[5] is connected with vertex[0]? True
If vertex[7] is connected with vertex[0]? False
调用上一节实现的无向图,运行即完成了DFS
附上搜寻的图:

广度优先搜索(Breadth First Search)
定义
从示例来理解
- BFS是一种用于遍历或搜寻树类或图类数据结构的算法,这种算法从根结点出发(如果是图,则任意选择一个顶点作为根结点),有时会引用“搜索键”,来对当前所有相邻结点优先于下一层结点的顺序进行遍历或搜索。
- BFS类似树中的层次遍历
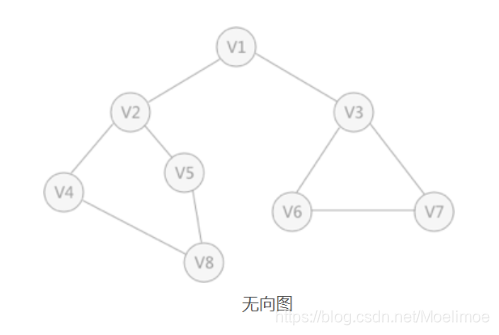
假设从V1结点出发,则遍历顺序是:V1→V2→V3→V4→V5→V6→V7→V8
从即将实现的代码设计中理解
- 回想树的层序遍历(layer_ergodic)中,遍历时借助了一个辅助队列
- 将根结点存入到辅助队列,然后将队列中的元素弹出来
- 弹出来发现它有子结点,将左右子结点先后放入到辅助队列,然后继续弹出一个结点
- 为左子结点,判断其是否还有子结点,有则放入队列
- 同样的对右子结点进行弹出判断。。。以此类推,直到没有元素可弹为止
主要方法与属性设计
与DFS相同的设计属性就不重复介绍了
- self.queue BFS的辅助队列
- bfs() 对传入类中的图进行广度优先遍历
Python代码实现
from Structure.graph.Undigraph import Undigraphclass BreadthFirstSearch:def __init__(self, graph, x):self.graph = graphself.marked = [False for _ in range(self.graph.vertex)]self.count = 0self.queue = []self.bfs(x)# self.dfs1(x)def is_marked(self, x):return self.marked[x]def bfs(self, x):self.marked[x] = Trueself.queue += self.graph.v_edges[x]while self.queue:next_vertex = self.queue.pop(0)if self.is_marked(next_vertex):continueprint(f"Next vertex is {next_vertex}")self.marked[next_vertex] = Trueif self.graph.v_edges[next_vertex]:self.queue += self.graph.v_edges[next_vertex]self.count += 1self.count += 1def count_all_connected(self):return self.countif __name__ == '__main__':UG = Undigraph(13)UG.add_edge(0, 5)UG.add_edge(0, 1)UG.add_edge(0, 2)UG.add_edge(0, 6)UG.add_edge(5, 3)UG.add_edge(5, 4)UG.add_edge(3, 4)UG.add_edge(4, 6)UG.add_edge(7, 8)UG.add_edge(9, 10)UG.add_edge(9, 11)UG.add_edge(9, 12)UG.add_edge(11, 12)vertex1 = 0BFS = BreadthFirstSearch(UG, vertex1)print(f"Count all the vertices connected with the vertex[{vertex1}]: {BFS.count_all_connected()}")vertex2 = 3print(f"If vertex[{vertex2}] is connected with vertex[{vertex1}]? {BFS.is_marked(vertex2)}")vertex3 = 7print(f"If vertex[{vertex3}] is connected with vertex[{vertex1}]? {BFS.is_marked(vertex3)}")
运行结果
Next vertex is 5
Next vertex is 1
Next vertex is 2
Next vertex is 6
Next vertex is 3
Next vertex is 4
Count all the vertices connected with the vertex[0]: 7
If vertex[3] is connected with vertex[0]? True
If vertex[7] is connected with vertex[0]? False
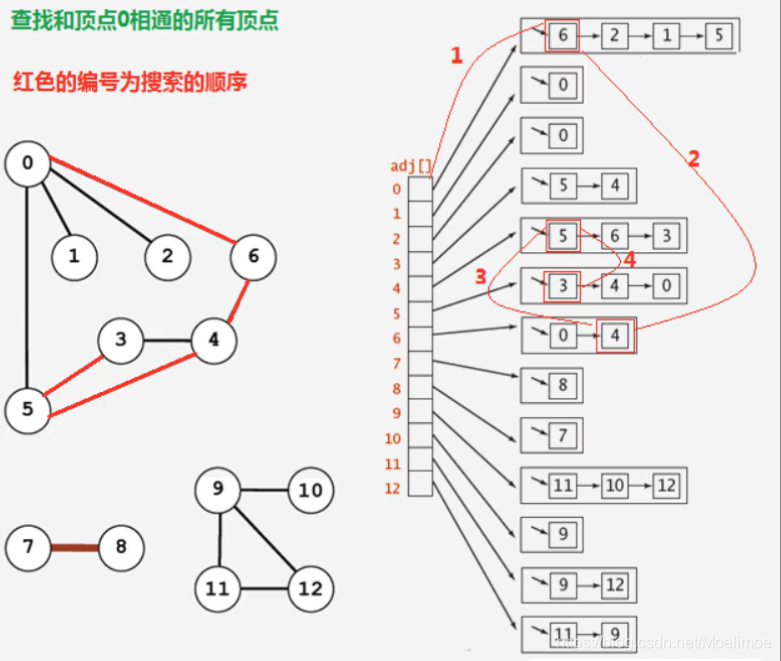
搜寻结果是 (0),5,1,2,6,3,4符合广度优先遍历顺序
附上搜寻的图:






 empty() in function cv::CascadeClassifier)
)







简介:定义+ 感知机+历史)




