加权无向图与prim算法和Kruskal算法寻找最小生成树

加权无向图的介绍

引入

• 加权无向图是一种为每条边关联一 个权重值或 是成本的图模型。这种图能够自然地表示许多应用。在一副航空图中,边表示航线,权值则可以表示距离或是费用。在一副电路图中,边表示导线,权值则可能表示导线的长度即成本,或是信号通过这条先所需的时间。此时我们很容易就能想到,最小成本的问题,例如,从西安飞纽约,怎样飞才能使时间成本最低或者是金钱成本最低?
  
• 给图的边赋予一定的权重标准，构成加权无向图

加权无向图中的边我们就不能简单向之前一样使用v-w两个顶点表示了（之前的adj_list列表中存放的是顶点，而必须要给边关联一个权重值，因此我们可以使用对象来描述一条边（现在要存放边对象Edge）。

构造加权无向边

属性及方法设计

1. 构造方法__init__()中
   vertex1和vertex2分别表示要构造的边的两端的顶点；weight表示要构造的边的权重
2. get_weight()获取边的权重
3. either() 获取当前边的其中一个顶点
4. opposite(v) 获取指定顶点的相反方向的顶点（以当前边对象Edge为媒介，存在唯一的相反方向的顶点），一般用在获取了一个顶点之后
5. compare(edge) 比较传入的Edge对象的权重和自身的权重，自身权重大返回1，两者相等返回0，否则返回-1

加权无向边Python代码实现

class Edge:def __init__(self, vertex1, vertex2, weight):self.vertex1 = vertex1self.vertex2 = vertex2self.weight = weightdef get_weight(self):return self.weightdef either(self):"""Return either vertex of this Edge"""return self.vertex1def opposite(self, v):return self.vertex1 if v == self.vertex2 else self.vertex2def compare(self, edge):return 1 if self.weight > edge.weight else (-1 if self.weight < edge.weight else 0)

代码较简单，测试就略过了，这里实现的Edge对象将用于后面的类方法实现。

Prim算法跳转
Kruskal算法跳转

Python代码实现加权无向图

from Structure.graph.Edge import Edgeclass WeightedUndigraph:def __init__(self, v):self.num_vertices = vself.num_edges = 0self.adj_list = [[] for _ in range(v)]def get_num_vertices(self):return self.num_verticesdef get_num_edges(self):return self.num_edgesdef add_edge(self, edge: Edge):v1 = edge.either()v2 = edge.opposite(v1)self.adj_list[v1].append(edge)self.adj_list[v2].append(edge)self.num_edges += 1def adjacent_edges(self, vertex):return self.adj_list[vertex]def all_edges(self):all_edges = []for i in range(self.num_vertices):for edge in self.adj_list[i]:if edge.opposite(i) < i:      all_edges.append(edge)return all_edges

最小生成树的介绍

引入
举例

• 省领导审查全省各市，如何找出最优最快路径完成审查
• 所有连接这些城市的道路中，路径(权重)最短的则是最优路径，此时要用到最小生成树

最小生成树的定义

• 最小生成树（Minimum spanning tree）或说最小权重生成树（Minimum weight spanning tree），是一幅连通的加权无向图中所有的边集合的一个子集，并且这些边必须连接所有顶点，这个子集它必须是无环的、权重和是最小的
• 对于连通图，一个图中可能有多颗生成树，最小生成树其实是最小权重生成树的简称。
• 广义上而言，对于非连通无向图来说，它的每一连通分量同样有最小生成树，它们的并被称为最小生成森林。

约定

1. 只考虑连通图。最小生成树的定义说明它只能存在于连通图中,如果图不是连通的,那么分别计算每个连通图子图的最小生成树，合并到一起称为最小生成森林。
   因为非连通图，无法找出连接全部顶点的边
2. 所有边的权重都各不相同。如果不同的边权重可以相同,那么一 副图的最小生成树就可能不唯一 了 ,虽然我们的算法可以处理这种情况,但为了好理解,我们约定所有边的权重都各不相同。

最小生成树的性质

• 用一条边连接最小生成树中的任意两个(不相邻的)顶点都会产生一 个新的环;
  
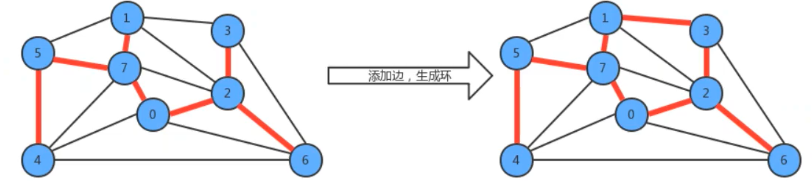
• 删除最小生成树的任意一条边,将会得到两棵独立的树；
  

寻找最小生成树（Minimum Spanning Tree）

在实现寻找最小生成树之前，我们先来了解一下实现寻找最小生成树的两个原理

切分定理

切分定理
先了解概念
要从一副连通图中找出该图的最小生成树,需要通过切分定理完成。

• 切分:将图的所有顶点按照某些规则分为两个非空且没有交集的集合。
• 横切边:连接两个属于不同集合的顶点的边称之为横切边。
  例如我们将图中的顶点切分为两个集合,色顶点于一个集合,色顶点属于外一个集合,那么效果如下:
  

再了解定义
切分定理:

• 在一副加权图中, 给定任意的切分,它的横切边中的权重最小者必然属于图中的最小生成树。
  
• 注意:一次切分产生的多个横切边中,权重最小的边不一定是所有横切边中唯一属于图的最小生成树的边。也有可能非最小权重的横切边也是最小生成树的边

贪心算法（Greedy Algorithm）

定义

• 任何在想要寻找全局最优方法时，在所有单个阶段进行探索时都尝试寻找当前阶段的局部最优解，以尝试获取最终的全局最优解，这样的算法都可以称之为贪心算法。
• 在许多问题中，贪心算法的思想并不能总是获得一个最优解，但是贪心算法的探索过程，会生成许多的局部最优解，这些局部最优解在合理的时间内，也可以近似地等于一个全局最优解

Prim算法

计算图的最小生成树的算法有很多种,但这些算法都可以看做是贪心算法的一种特殊情况,这些算法的不同之处在于保存切分和判定权重最小的横切边的方式。

prim算法定义

• prim算法是一种用于寻找加权无向图中最小生成树的贪心算法，prim算法选择随机的一个顶点开始，把这个顶点当做处于MST的集合，而把其他不在这颗MST中的顶点标记为不处于MST中的集合，然后通过不断的重复做某些操作，可以逐渐将非最小生成树中的顶点加入到最小生成树中，直到所有的顶点都加入到最小生成树中。

Prim算法的切分规则:

• 把最小生成树中的顶点看做是一个集合 ,把不在最小生成树中的顶点看做是另外一个集合。
• 最开始是把任意一个结点当做最小生成树的结点；而剩下的其他结点则不是树中的结点
  

在实现prim算法寻找MST之前，我们要借助一个最小索引优先队列，来方便地取出最小权重边：

• 引入索引最小优先队列the_cut_edges，它的索引代表图的顶点，储存的值代表从其他的某个顶点到当前索引对应顶点的边的权重，当遍历完某个顶点的邻接边时，the_cut_edges就会储存所有该顶点通向其他顶点的边的权重（重复的权重后面会有设计方法来避免），当最后遍历完时，我们只需要调用索引最小优先队列的delete_min_and_get_index()即可获取最小权重对应的顶点
  

索引最小有限队列代码传送门
加权无向边，up↑
加权无向图，up↑

Prim算法Python代码实现寻找MST

from Structure.graph.WeightedUndigraph import WeightedUndigraph
from Structure.graph.Edge import Edge
from Structure.PriorityQueue.IndexMinpriorutyQueue import IndexMinPriorityQueue
from math import infclass PrimMST:def __init__(self, graph):"""MST here represent the Minimum Spanning Tree of the current loop"""self.graph = graph# Memorize the cheapest edge to MST of each vertex(index)self.min_edge_to_MST = [None for _ in range(self.graph.get_num_vertices())]# Store the smallest weight of each vertex(index)'s edge to MST;# Initialize it with infinite plus, we will compare out a minimum weight afterself.min_weight_to_MST = [+inf for _ in range(self.graph.get_num_vertices())]# Mark a True if a vertex(index) has been visitedself.marked = [False for _ in range(self.graph.get_num_vertices())]# Memorize the smaller weight of each vertex(index)'s edge connected to MSTself.the_cut_edges = IndexMinPriorityQueue(self.graph.get_num_vertices())# Initialize a 0.0 as the minimum weight to weight_to_MSTself.min_weight_to_MST[0] = 0.0self.the_cut_edges.insert(0, 0.0)while not self.the_cut_edges.is_empty():# Take out the minimum-weighted vertex, and make a visit(update) for itself.visit(self.the_cut_edges.delete_min_and_get_index())def visit(self, v):"""Update the MST"""self.marked[v] = Truefor e in self.graph.adjacent_edges(v):w = e.opposite(v)# Check if the opposite vertex of v in edge e is marked, if did, skip this loopif self.marked[w]:continue# Find out the minimum-weighted-edge vertex opposite to this vertex(v)if e.get_weight() < self.min_weight_to_MST[w]:    # e.get_weight():Get weight of the edge between v and w# Update the minimum edge and weight# print(f"v: {v}, w: {w}, min_weight_edge: {e.get_weight()}")self.min_edge_to_MST[w] = eself.min_weight_to_MST[w] = e.get_weight()if self.the_cut_edges.is_index_exist(w):# print(w, e.get_weight())self.the_cut_edges.change_item(w, e.get_weight())else:self.the_cut_edges.insert(w, e.get_weight())def min_weight_edges(self):return [edge for edge in self.min_edge_to_MST if edge]if __name__ == '__main__':with open('../MST.txt', 'r') as f:num_vertices = int(f.readline())num_edges = int(f.readline())graph = WeightedUndigraph(num_vertices)for e in range(num_edges):v1, v2, w = f.readline().split()graph.add_edge(Edge(int(v1), int(v2), float(w)))P_MST = PrimMST(graph)for e in P_MST.min_weight_edges():v = e.either()w = e.opposite(v)weight = e.weightprint(f"v: {v} w: {w} weight: {weight}")

运行结果

v: 1 w: 7 weight: 0.19
v: 0 w: 2 weight: 0.26
v: 2 w: 3 weight: 0.17
v: 4 w: 5 weight: 0.35
v: 5 w: 7 weight: 0.28
v: 6 w: 2 weight: 0.4
v: 0 w: 7 weight: 0.16

即是最小生成树的所有边的权重和

MST.txt

8
16
4 5 0.35
4 7 0.37
5 7 0.28
0 7 0.16
1 5 0.32
0 4 0.38
2 3 0.17
1 7 0.19
0 2 0.26
1 2 0.36
1 3 0.29
2 7 0.34
6 2 0.40
3 6 0.52
6 0 0.58
6 4 0.93

Kruskal算法

定义

• kruskal算法图论中寻找加权无向图的最小生成树的另一种贪心算法，它的主要思想是按照边的权重(从小到大)处理它们，将边加入最小生成树中,加入的边不会与已经加入最小生成树的边构成环,直到树中含有N-1条边为止。

kruskal算法和prim算法的区别:

• Prim算法是一次一条边的构造最小生成树,每一步都为一棵树添加一条边。kruskal算法构造最小生成树的时候也是一次一条边地构造,但它的切分规则是不一样的。它每一次寻找的边会连接一片森林中的两棵树。如果一副加权无向图由V个顶点组成 ,初始化情况下每个顶点都构成一棵独立的树,则V个顶点对应V棵树,组成一片森林, kruskal算法每一次处理都会将两棵树合并为一棵树,直到整个森林中只剩一棵树为止。

实现步骤：

Kruskal算法在寻找MST时，需要用到并查集来实现，当寻找的树不是连通的时候（初始时所有结点都是分隔开的），它就会为在每一颗树中搜寻出一个MST。

主要属性和方法设计

1. 构造方法__init__()中
   UFT是一个优化后的并查集UF_Tree_Weighted对象，索引代表顶点，使用其in_the_same_group(v, w)可以判断两个顶点是否在同一颗树上，使用其unite()方法可以将两个顶点所在的树合并
   all_edges 是一个最小优先队列MinPriorityQueue的对象，储存图中所有的边，并使用最小优先队列进行按照权重对边进行排序
   edges_MST 是一个列表（当做队列），储存了MST的所有边，get_all_edges_mst()返回的就是它，可以直观地观察MST的边
2. 生成MST的方法直接在构造方法中实现，调用即可完成

并查集传送、
最小优先队列传送（最小优先队列需要小小地修改比较的方法，应该比较传入的Edge对象的weight，否则直接比较会报错）：

    def less(self, i, j):return operator.lt(self.heap[i].weight, self.heap[j].weight)

优化后的并查集传送
最小优先队列传送
加权无向边
加权无向图

Kruskal算法Python代码寻找MST

from Structure.UF.UF_Tree_Weighted import UF_Tree_Weighted
from Structure.PriorityQueue.MinPriorityQueue import MinPriorityQueue
from Structure.graph.WeightedUndigraph import WeightedUndigraph
from Structure.graph.Edge import Edgeclass KruskalMST:def __init__(self, graph):self.graph = graphself.N = self.graph.num_verticesself.UFT = UF_Tree_Weighted(self.N)self.all_edges = MinPriorityQueue()self.edges_MST = []for e in self.graph.get_all_edges():self.all_edges.append(e)while not self.all_edges.is_empty() and len(self.edges_MST) < self.N - 1:min_edge = self.all_edges.extract_min()v = min_edge.either()w = min_edge.opposite(v)if self.UFT.in_the_same_group(v, w):continueself.UFT.unite(v, w)self.edges_MST.append(min_edge)def get_all_edges_mst(self):return self.edges_MSTif __name__ == '__main__':with open('../MST.txt', 'r') as f:num_vertices = int(f.readline())num_edges = int(f.readline())graph = WeightedUndigraph(num_vertices)for e in range(num_edges):v1, v2, w = f.readline().split()graph.add_edge(Edge(int(v1), int(v2), float(w)))K_MST = KruskalMST(graph)for e in K_MST.get_all_edges_mst():v = e.either()w = e.opposite(v)weight = e.weightprint(f"v: {v} w: {w} weight: {weight}")

运行结果：

v: 0 w: 7 weight: 0.16
v: 2 w: 3 weight: 0.17
v: 1 w: 7 weight: 0.19
v: 0 w: 2 weight: 0.26
v: 5 w: 7 weight: 0.28
v: 4 w: 5 weight: 0.35
v: 6 w: 2 weight: 0.4

MST.txt

8
16
4 5 0.35
4 7 0.37
5 7 0.28
0 7 0.16
1 5 0.32
0 4 0.38
2 3 0.17
1 7 0.19
0 2 0.26
1 2 0.36
1 3 0.29
2 7 0.34
6 2 0.40
3 6 0.52
6 0 0.58
6 4 0.93